The Nature of Philosophy

Readers (including, often, myself) have a bad habit of skipping introductions, as if they were irrelevant afterthoughts to the book they are about to spend a considerable amount of time with. Instead, introductions — at the least when carefully thought out — are crucial reading keys to the text, setting the stage for the proper understanding (according to the author) of what comes next. This introduction is written in that spirit, so I hope you will begin your time with this book by reading it first.

As the quote above from Epictetus reminds us, the ancient Stoics made a big deal of differentiating what is in our power from what is not in our power, believing that our focus in life ought to be on the former, not the latter. Writing this book the way I wrote it, or in a number of other possible ways, is in my power. How people will react to it, is not in my power. Nonetheless, it will be useful to set the stage and acknowledge some potential issues right at the outset, so that any disagreement will be due to actual divergence of opinion, not to misunderstandings.

The central concept of the book is the idea of “progress” and how it plays in different disciplines, specifically science, mathematics, logic and philosophy — which I see as somewhat allied fields, though each with its own crucial distinctive features. Indeed, a major part of this project is to argue that science, the usual paragon for progress among academic disciplines, is actually unusual, and certainly distinct from the other three. And I will argue that philosophy is in an interesting sense situated somewhere between science on the one hand and math and logic on the other hand, at the least when it comes to how these fields make progress.

But I am getting slightly ahead of myself. One would think that progress is easy to define, yet a cursory look at the literature would quickly disabuse you of that hope (as we will appreciate in due course, there is plenty of disagreement over what the word means even when narrowly applied to the seemingly uncontroversial case of science). As it is often advisable in these cases, a reasonable approach is to go Wittgensteinian and argue that “progress” is a family resemblance concept. Wittgenstein’s own famous example of this type of concept was the idea of “game,” which does not admit of a small set of necessary and jointly sufficient conditions in order to be defined, and yet this doesn’t seem to preclude us from distinguishing games from not-games, at least most of the time. In his Philosophical Investigations (1953 / 2009), Wittgenstein begins by saying “consider for example the proceedings that we call ‘games’ ... look and see whether there is anything common to all.” (§66) After mentioning a number of such examples, he says: “And we can go through the many, many other groups of games in the same way; we can see how similarities crop up and disappear. And the result of this examination is: we see a complicated network of similarities overlapping and criss-crossing: sometimes overall similarities.” Hence: “I can think of no better expression to characterize these similarities than ‘family resemblances’; for the various resemblances between members of a family: build, features, colour of eyes, gait, temperament, etc. etc. overlap and criss-cross in the same way. And I shall say: ‘games’ form a family.” (§67) Concluding: “And this is how we do use the word ‘game.’ For how is the concept of a game bounded? What still counts as a game and what no longer does? Can you give the boundary? No. You can draw one; for none has so far been drawn. (But that never troubled you before when you used the word ‘game.’)” (§68)

Progress, then, can be thought of to be like pornography (to paraphrase the famous quip by US Supreme Court Justice Potter Stewart): “I know it when I see it.” But perhaps we can descend from the high echelons of contemporary philosophy and jurisprudence and simply do the obvious thing: look it up in a dictionary. For instance, from the Merriam- Webster we get:

i. “forward or onward movement toward a destination”

ii. or: “advancement toward a better, more complete, or more modern condition”

with the additional useful information that the term originates from the Latin (via Middle English) progressus, which means “an advance” from the verb progredi: pro for forward and gradi for walking.

How is that going to help? I will defend the proposition that progress in science is a teleonomic (i.e., goal oriented) process along definition (i), where the goal is to increase our knowledge and understanding of the natural world. Even though we shall see that there are a lot more complications and nuances that need to be discussed in order to agree with that general conclusion, I believe this captures what most scientists and philosophers of science mean when they say that science, unquestionably, makes progress.

Definition (ii), however, is more akin to what I think has been going on in mathematics, logic and (with an important qualification to be made in a bit), philosophy. Consider first mathematics (and, by similar arguments, logic): since I do not believe in a Platonic realm where mathematical and logical objects “exist” in any meaningful, mind-independent sense of the word (more on this later), I therefore do not think mathematics and logic can be understood as teleonomic disciplines (fair warning to the reader, however: many mathematicians and a number of philosophers of mathematics do consider themselves Platonists). Which means that I don’t think that mathematics pursues an ultimate target of truth to be discovered, analogous to the mapping on the kind of external reality that science is after. Rather, I think of mathematics (and logic) as advancing “toward a better, more complete” position, “better” in the sense that the process both opens up new lines of internal inquiry (mathematical and logical problems give origin to new — internally generated — problems) and “more complete” in the sense that mathematicians (and logicians) are best thought as engaged in the exploration of what throughout the book I call a space of conceptual (as distinct from empirical) possibilities.

How do we cash out this idea of a space of conceptual possibilities? And is such a space discovered or invented? During the first draft of this book I was only in a position to provide a sketched, intuitive answer to these questions. But then I came across Peter Unger and Lee Smolin’s The Singular Universe and the Reality of Time: A Proposal in Natural Philosophy (2014), where they provide what for me is a highly satisfactory answer in the context of their own discussion of the nature of mathematics. Let me summarize their arguments, because they are crucial to my project as laid out in this book.

In the second part of their tome (which was written by Smolin, Unger wrote the first part), Chapter 5 begins by acknowledging that some version of mathematical Platonism — the idea that “mathematics is the study of a timeless but real realm of mathematical objects,” is common among mathematicians (and, as I said, philosophers of mathematics), though by no means universal, and certainly not uncontroversial. The standard dichotomy here is between mathematical objects (a term I am using loosely to indicate any sort of mathematical construct, from numbers to theorems, etc.) being discovered (Platonism) vs being invented (nominalism and similar positions: Bueno 2013).

Smolin immediately proceeds to reject the above choice as an example of false dichotomy: it is simply not the case that either mathematical objects exist independently of human minds and are therefore discovered, or that they do not exist prior to our making them up and are therefore invented. Smolin presents instead a table with four possibilities:

“Discovered”: prior existence	rigid properties
“Fictional”: prior existence	non-rigid properties
“Evoked”: no prior existence	rigid properties
“Invented”: no prior existence	non-rigid properties

By “rigid properties” here Smolin means that the objects in question present us with “highly constrained” choices about their properties, once we become aware of such objects. Let’s begin with the obvious entry in the table: when objects exist prior to humans thinking about them, and they have rigid properties. All scientific discoveries fall into this category: planets, say, exist “out there” independently of anyone being able to verify this fact, so when we become capable of verifying their existence and of studying their properties we discover them.

Objects that had no prior existence, and are also characterized by no rigid properties include, for instance, fictional characters (Smolin calls them “invented”). Sherlock Holmes did not exist until the time Arthur Conan Doyle invented (surely the appropriate term!) him, and his characteristics are not rigid, as has been (sometimes painfully) obvious once Holmes got into the public domain and different authors could pretty much do what they wanted with him (and I say this as a fan of both Robert Downey Jr. and Benedict Cumberbatch). Smolin, unfortunately, doesn’t talk about the “fictional” category of his classification, which comprises objects that had prior existence and yet are not characterized by rigid properties. Perhaps some scientific concepts, such as that of biological species, fall into this class: “species,” however one conceives of them, certainly exist in the outside world; but how one conceives of them (i.e., what properties they have) may depend on a given biologist’s interests (this is referred to as pluralism about species concepts in the philosophy of biology: Mishler & Donoghue 1982).

The crucial entry in the table, for our purposes here, is that of “evoked” objects: “Why could something come to exist, which did not exist before, and, nonetheless, once it comes to exist, there is no choice about how its properties come out? Let us call this possibility evoked. Maybe mathematics is evoked” (Unger and Smolin, 2014, 422). Smolin goes on to provide an uncontroversial class of evocation, and just like Wittgenstein, he chooses games: “For example, there are an infinite number of games we might invent. We invent the rules but, once invented, there is a set of possible plays of the game which the rules allow. We can explore the space of possible games by playing them, and we can also in some cases deduce general theorems about the outcomes of games. It feels like we are exploring a pre-existing territory as we often have little or no choice, because there are often surprises and incredibly beautiful insights into the structure of the game we created. But there is no reason to think that game existed before we invented the rules. What could that even mean?” (p. 422)

Interestingly, Smolin includes forms of poetry and music into the evoked category: once someone invented haiku, or the blues, then others were constrained by certain rules if they wanted to produce something that could reasonably be called haiku poetry, or blues music. An obvious example that is very close to mathematics (and logic) itself is provided by board games: “When a game like chess is invented a whole bundle of facts become demonstrable, some of which indeed are theorems that become provable through straightforward mathematical reasoning. As we do not believe in timeless Platonic realities, we do not want to say that chess always existed — in our view of the world, chess came into existence at the moment the rules were codified. This means we have to say that all the facts about it became not only demonstrable, but true, at that moment as well ... Once evoked , the facts about chess are objective, in that if any one person can demonstrate one, anyone can. And they are independent of time or particular context: they will be the same facts no matter who considers them or when they are considered” (p. 423).

This struck me as very powerful and widely applicable. Smolin isn’t simply taking sides in the old Platonist / nominalist debate about the nature of mathematics. He is significantly advancing that debate by showing that there are two other cases missing from the pertinent taxonomy, and that moreover one of those cases provides a positive account of mathematical (and similar) objects, rather than just a rejection of Platonism. But in what sense is mathematics analogous to chess? Here is Smolin again: “There is a potential infinity of formal axiomatic systems (FASs). Once one is evoked it can be explored and there are many discoveries to be made about it. But that statement does not imply that it, or all the infinite number of possible formal axiomatic systems, existed before they were evoked. Indeed, it’s hard to think what belief in the prior existence of a FAS would add. Once evoked, a FAS has many properties which can be proved about which there is no choice — that itself is a property that can be established. This implies there are many discoveries to be made about it. In fact, many FASs once evoked imply a countably infinite number of true properties, which can be proved” (p. 425).

Reflecting on the category of evoked objective truths provided me with a reading key to make sense of what I was attempting to articulate: my suggestion here, then, is that Smolin’s account of mathematics applies, mutatis mutandis (as philosophers are wont to say) to logic and, with an important caveat, to philosophy. All these disciplines — but, crucially, not science — are in the business of ascertaining “evoked,” objective truths about their subject matters, even though these truths are neither discovered (in the sense of corresponding to mind independent states of affairs in the outside world) nor invented (in the sense of being (entirely) arbitrary constructs of the human mind).

I have referred twice already to the idea that philosophy is closer to mathematics and logic (and a bit further from science) via a qualification. That qualification is that philosophy is, in fact, concerned directly with the state of the world (unlike mathematics and logic, which while very useful to scientists, could be, and largely are, pursued without any reference whatsoever to how the world actually is). If you are doing ethics, or political philosophy, for instance, you are very much concerned with those aspects of the world that deal with interactions among humans within the context of their societies. If you are doing philosophy of mind you are ultimately concerned with how actual human (and perhaps artificial) brains work and generate consciousness and intelligence. Even if you are a metaphysician — engaging in what is arguably the most abstract field of philosophical inquiry — you are still trying to provide an account of how things hang together, so to speak, in the real cosmos. This means that the basic parameters that philosophers use as their inputs, the starting points of their philosophizing, their equivalent of axioms in mathematics and assumptions in logic (or rules in chess) are empirical data about the world. This data comes from both everyday experience (since the time of the pre-Socratics) and of course increasingly from the world of science itself. Philosophy, I maintain, is in the business of exploring the sort of conceptually evoked spaces that Smolin is talking about, but the evocation is the result of whatever starting assumptions are made by individual philosophers working within a particular field and, crucially, of the constraints that are imposed by our best understanding of how the world actually is.

I hope it is clear from the above analysis that I am not suggesting that every field that can be construed as somehow exploring a conceptual space ipso facto makes progress. If that were the case, we would be forced to say that pretty much everything humans do makes progress. Consider, for instance, fiction writing. Specifically, imagine a science fiction author who writes three books about the same planet existing in three different “time lines.” [1] In each book, the geography of the planet is different, which leads to different evolutionary paths for its inhabitants. However, each description is constrained by the laws of physics (he wants to keep things in accordance with those laws), by some rational principles (the same object can’t be in two places, as that would violate the principle of non-contradiction), and perhaps even by certain aesthetic principles. Each book tells a different story, constrained both empirically (laws of physics), and logically. In a sense, this writer would be exploring different conceptual spaces, by describing different possibilities unfolding on the fictitious planet. However, I do not think that we want to say that he is making progress. He is just exploring various imaginary worlds. The difference with philosophy, then, is twofold: i) our writer is doing what Smolin calls “inventing”: his worlds did not have prior existence to his imagining them, and they have no rigid properties. Even the constraints he imposes from the outset, both empirical and logical, could have been otherwise. He could have easily imagined planets where both the laws of physics and those of logic are different. Philosophy, I maintain, is in the business of doing empirically-informed evoking, not inventing, which means that its objects of study have rigid properties. ii) Philosophy, again, is very much concerned with the world as it is, not with arbitrarily invented ones. Even when philosophers venture into thought experiments, or explore “possible worlds” they do so with an interest to figure things out as far as this world is concerned. So, no, I am not suggesting that every human activity makes progress, nor that philosophy is like literature.

There are two additional issues I want to take up right at the beginning of this book, though they will reappear regularly throughout the volume. They both, I think, contribute to much confusion and perplexity whenever the topic of progress in philosophy comes up for discussion. The first issue is that philosophers too often use the word “theory” to refer to what they are doing, while in fact our discipline is not in the business of producing theories — if by that one means complex and testable explanations of how the world works. The word “theory” immediately leads one to think of science (though, of course, there are mathematical theories too). In light of what I have just argued about the teleonomic nature of scientific progress contrasted with the exploratory / qualificatory nature of philosophical inquiry, one can see how talking about philosophical “theories” may not be productive. Philosophers do have an alternative term, which gets used quite often interchangeably with “theory”: account. I much prefer the latter, and will make an effort to drop the former altogether. “Account” seems a more appropriate term because philosophy — the way I see it — is in the business of clarifying things, or analyzing in order to bring about understanding, not really discovering new facts, but rather evoking rational conclusions arising from certain ways of looking at a given problem or set of facts.

The second issue is a way to concede an important point to critics of philosophy (which include a number of scientists and, surprisingly, philosophers themselves). I am proposing a model of philosophical inquiry conceived as being in the business of providing accounts of evoked truths by exploring and refining our understanding of a series of conceptual landscapes. But it is true that such refinement can at some point begin to yield increasingly diminishing returns, so that certain discussion threads become more and more limited in scope, ever more the result of clever logical hair splitting, and of less and less use or interest to anyone but a vanishingly small group of professionals who, for whatever reason, have become passionate about it. A good example of this, I think, is the field of “gettierology,” which has resulted from discussions on the implications of a landmark (very short) paper published by Edmund Gettier back in 1963, a paper that for the first time questioned the famous concept of knowledge as justified true belief often attributed (with some scholarly disagreement) to Plato. We will examine Gettier’s paper and its aftermath as an example of progress in philosophy later on, but it has to be admitted that more than half a century later pretty much all of the interesting things that could have possibly been said in response to Gettier are likely to have been said, and that ongoing controversies on the topic lack relevance and look increasingly self-involved.

However, I will also immediately point out that this problem isn’t specific to philosophy: pretty much every academic field — from literary criticism to history, from the social sciences to, yes, even the natural sciences — suffer from the same malaise, and examples are not hard to find. I spent a large amount of my academic career as an evolutionary biologist, and I cannot vividly enough convey the sheer boredom at sitting through yet another research seminar when someone was presenting lots of data that simply confirmed once again what everyone already knew, except that the work had been carried out on a species of organisms for which it hadn’t been done before. Since there are (conservatively) close to nine million species on our planet, you can see the potential for endless funding and boundless irrelevancy. At the least philosophical scholarship is very cheap by comparison with even the least expensive research program in the natural sciences!

Before concluding this overview and inviting you to plunge into the main part of the book, let me briefly discuss some of the surprisingly few papers written by philosophers over the years that explicitly take up the question of progress in their field, as part of scholarship in so-called “metaphilosophy.” I have chosen three of these papers as representative of the (scant) available literature: Moody (1986), Dietrich (2011) and Chalmers (2015). [2] The first one claims that there is indeed progress in philosophy, though with important qualifications, the second one denies it (also with crucial caveats), and the third one takes an intermediate position.

Moody (1986) distinguishes among three conceptions of progress: what he calls Progress-1 takes place when there is a specifiable goal about which people can agree that it has been achieved, or what counts towards achieving it. If you are on a diet, for instance, and decide to lose ten pounds, you have a measurable specific goal, and you can be said to make progress insofar your weight goes down and approaches the specific target (and, of course, you can also measure your regress, should your weight go further up!). Progress-2 occurs when one cannot so clearly specify a goal to be reached, and yet an individual or an external observer can competently judge that progress (or regress) has occurred when comparing the situation a time t vs the situation at time t+1, even though the criteria by which to make that judgment are subjective. Moody suggests, for example, that a composer guided by an inner sense of when they are “getting it right” would be making this sort of progress while composing. Finally, Progress-3 is a hybrid animal, instantiated by situations where there are intermediate but not overarching goals. Interestingly, Moody says that mathematics makes Progress-3, insofar as there is no overall goal of mathematical scholarship, and yet mathematicians do set intermediate goals for themselves, and the achievement of these goals (like the proof of Fermat’s Last Theorem) are recognized as such by the mathematical community. (Moody says that science too makes Progress-3, although as we have discussed before, science actually does have an ultimate, specifiable goal: understanding and explaining the natural world. So I would rather be inclined to say that science makes Progress-1, within Moody’s scheme.)

Moody’s next step is to provisionally assume that philosophy is a type of inquiry, and then ask whether any of his three categories of progress apply to it. The first obstacle is that philosophy does not appear to have consensus-generating procedures such as those found in the natural sciences or in technological fields like engineering. So far so good for my own account given above, since I distinguish progress in the sciences from progress in other fields, particularly philosophy. Moody claims (1986, 37) that “the only thing that philosophers are likely to agree about with enthusiasm is the abysmal inadequacy of a particular theory.” While I think that is actually a bit too pessimistic (we will see that philosophers agree — as a plurality of opinions — on much more than they are normally given credit for), I do not share Moody’s pessimistic assessment of that observation: negative progress, i.e., the elimination of bad ideas, is progress nonetheless. Interestingly, Moody remarks (again, with pessimism that is not warranted in my mind) that in philosophy people talk about “issues” and of “positions,” not of the scientific equivalent “hypotheses” and “results.” I think that is because philosophy is not sufficiently akin to science for the latter terms to make sense within discussions of philosophical inquiry.

Moody soon concludes that philosophy does not make Progress-1 or Progress-3, because its history has not yielded a trail of solved problems. What about Progress-2? Here the discussion is interesting though somewhat marginal to my own project. Moody takes up the possibility that perhaps philosophy is not a type of inquiry after all, and analyzes in some detail two alternative conceptions: Wittgenstein’s (1965) idea of philosophy as “therapy” and Richard Rorty’s (1980) so-called “conversational model” of philosophy. As Moody (1986, 38) magisterially summarizes it: “Wittgenstein believed that philosophical problems are somehow spurious and that the activity of philosophy ... should terminate with the withdrawal, or deconstruction, of philosophical questions.” On this view, then, there is progress, of sorts, in philosophy, but it is the sort of “terminus” brought about by committing seppuku. As Moody rather drily comments, while nobody can seriously claim that Wittgenstein’s ideas have not been taken seriously, it is equally undeniable that philosophy has largely gone forward pretty much as if the therapeutic approach had never been articulated. If a proposed account of the nature of philosophy has so blatantly been ignored by the relevant epistemic community, we can safely file it away for the purposes of this book.

Rorty’s starting point is what he took to be the (disputable, in my opinion) observation that philosophy has failed at its self-appointed task of analysis and criticism. Moody quotes him as saying (1986, 39): “The attempts of both analytic philosophers and phenomenologists to ‘ground’ this and ‘criticize’ that were shrugged off by those whose activities were purportedly being grounded and criticized.” Rorty arrived at this because of his rejection of what he sees as philosophy’s “hangover” from the 17th and 18th centuries, when philosophers were attempting to set their inquiry within a framework that allowed a priori truths to be discovered (think Descartes and Kant), even though David Hume had dealt that framework a fatal blow already in the 18th century.

While Moody finds much of Rorty’s analysis on target, I must confess that I don’t, even though it does have some value. For instance, the fact that other disciplines (like science) marched on while refusing to be grounded or criticized by philosophy is neither entirely true (lots of scientists have paid and still pay a significant amount of attention to philosophy of science, for instance) nor should it necessarily be taken as the ultimate test of the value of philosophy even if true: creationists and climate change denialists, after all, shrug off any criticism of their positions, but that doesn’t make such criticism invalid, or futile for that matter (since others are responding to it). Yet, there is something to be said for thinking of philosophy as a “conversation” more than an inquiry, as Rorty did. The problem is that this and other dichotomies presented to us by Rorty are, as Moody himself comments, false: “we do not have to choose between ‘saying something,’ itself a rather empty notion that manages to say virtually nothing, and inquiring, or between ‘conversing’ and ‘interacting with nonhuman reality.’” Indeed we don’t.

But what account, then, can we turn to in order to make sense of progress in philosophy, according to Moody? I recommend the interested reader check Moody’s discussion of Robert Nozick’s (1981) “explanational model” of philosophy, as well as of John Kekes’ (1980) “perennial problems” approach, but my own treatment here will jump to Nicholas Rescher (1978) and the concept of “aporetic clusters,” which is one path that supports the conclusion — according to Moody — that philosophy does make progress, and it is a type-2 progress. Rescher thinks that it is unrealistic to expect consensus in philosophy, and yet does not see this as a problem, but rather as a natural outcome of the nature of philosophical inquiry (1986, 44): “in philosophy, supportive argumentation is never alternative-precluding. Thus the fact that a good case can be made out for giving one particular answer to a philosophical question is never considered as constituting a valid reason for denying that an equally good case can be produced for some other incompatible answers to this question.”

In fact, Rescher thinks that philosophers come up with “families” of alternative solutions to any given philosophical problem, which he labels aporetic clusters. [3] According to this view, some philosophical accounts are eliminated, while others are retained and refined. The keepers become philosophical classics, like “virtue ethics,” “utilitarianism” or “Kantian deontology” in ethics, or “constructive empiricism” and “structural realism” in philosophy of science. Rescher’s view is not at all incompatible with my idea of philosophy as evoking (to use the terminology introduced earlier), and then exploring and refining, peaks in conceptual landscapes. As Moody (1986, 45) aptly summarizes it: “that there are ‘aporetic clusters’ is evidence of a kind of progress. That the necrology of failed arguments is so long is further evidence.”

A very different take on all of this is what we get from the second paper I have selected to get our feet wet for our exploration of progress in philosophy and allied disciplines, the provocatively titled “There is no progress in philosophy,” by Eric Dietrich. The author does not mince words (to be sure, a professional hazard in philosophy, to which I am not immune myself), even going so far as diagnosing people who disagree with his contention that philosophy does not make progress with a mental disability, which he labels “anosognosia” “[a] condition where the affected person denies there is any problem.” I guess the reader should be warned that, apparently, I do suffer from anosognosia.

Dietrich begins by arguing that philosophy is in a relevant sense like science. Specifically, he draws a parallel between strong disagreements among philosophers on, say, utilitarianism vs deontology in ethics, with similarly strong, and lost lasting, disagreements among scientists about issues like group selection in evolutionary biology, or quantum mechanics during the early part of the 20th century. But, Dietrich then adds, philosophy is also relevantly dissimilar from science: scientific disagreements eventually get resolved and the enterprise lurches forward (every physicist nowadays accepts quantum mechanics, having abandoned Einstein’s famous skepticism about it — though this hasn’t happened yet for group selection, it must be pointed out). Philosophical disagreements, instead, have been more or less the same for 3000 years. Conclusion: philosophy does not make progress, it just “stays current,” meaning that it updates its discussions with the times (e.g., today we debate ethical questions surrounding gay rights, not those concerning slavery, as the latter is irrelevant, at the least in many parts of the world).

Dietrich acknowledges that modern philosophy contains many new notions, and lists a number of them (e.g., supervenience, possible worlds, and modal logic). But immediately dismisses the suggestion that these may represent advances in philosophical discourse as “lame.” His evidence is that there is no widespread agreement about any of these notions, so their introductions cannot possibly be seen as advances. It follows that those philosophers who insist in defending their field in this fashion are affected by the above mentioned mental condition.

The reader will have already seen that Dietrich’s point is actually well countered by the preceding discussion, and particularly the explanation put forth by Rescher for why we see aporetic clusters of positions in philosophy. I will develop my own rejection of Dietrich’s sweeping conclusion in terms of non-teleonomic progress instantiated as exploration and refinement of a series of conceptual spaces throughout much of this book. And I will present (empirical!) evidence that philosophers are more in agreement on a wide range of issues than Dietrich and others acknowledge, though the agreement is about the viability of different positions within a given aporetic cluster, not about a single “winning” theory — which makes sense once we conceptualize philosophy in the manner introduced above and to be developed in the following chapters.

But even simply considering Dietrich’s own examples, it is hard to see where exactly he gets the idea that there is overwhelming disagreement: I don’t know of logicians who differ on the validity of modal logic, though of course they will deploy it differently in pursuit of their own specific goals. Nor do I know of anyone who disagrees on the concepts of supervenience or possible worlds, though people do reasonably disagree on what such concepts entail vis-a-vis a number of specific philosophical questions. Dietrich makes his argument in part by way of a thought experiment in which he brings Aristotle back to life and has him attend a couple of college courses: he imagines the Greek finding himself astonished and bewildered in a class on basic physics, but very much at ease in a class in logic or metaphysics (all three subjects, of course, on which Aristotle had a great deal to write, 23 centuries ago). My own intuition, however, is a bit different (we will come back to the use and misuse of intuitions and thought experiments in philosophy). While I agree that Aristotle wouldn’t know what to make of quantum mechanics and general relativity, he would have a lot of catching up to do in order to understand modern logics (plural, as there is an ample variety of them), and even in metaphysics he would have to take at least a remedial course before jumping in with both feet (not to mention that he wouldn’t know what the name of the discipline refers to, since it was adopted after his death).

Dietrich then moves on to introduce another mental illness, apparently affecting a much smaller number of philosophers: nosognosia, a condition under which the patient knows that there is something wrong, but still has some trouble fully accepting the implications. He discusses two such philosophers: Thomas Nagel (1986) and Colin McGinn (1993). Both Nagel and McGinn conclude that philosophical problems are intractable, and, hence, that there is no such thing as philosophical progress. However, they arrive at this conclusion by different routes. For Nagel this is because of an irreconcilable conflict between first (subjective) and third (objective) person accounts. While science deals with the latter, philosophy has to tackle both, and this creates contradictions that cannot be overcome. Here is Dietrich’s summary of Nagel’s view (2011, 339):

“There are three points of view. From the subjective view, we get one set of answers to philosophy questions, and from the objective view, we get another, usually contradictory, set, and from a third view, from which one can see the answers of both the subjective and objective views, one can see that the subjective and objective answers are equally valid and equally true. Therefore, philosophy problems are intractable. Philosophy cannot progress because it cannot solve them.”

McGinn, instead, says that there are answers to philosophical problems, but these — for some mysterious reason — are beyond human reach. Again, Dietrich’s summary (2011, 339):

“There are two relevant points of view. From one, the human view, philosophy problems are intractable. From the other, the alien view, philosophy problems are tractable (perhaps even trivial). The situation here is exactly like the situation with dogs and [the] English [language]. We easily understand it. Dogs understand only a tiny number of words, and seem to know nothing of combinatorial syntax. Therefore, though it is unlikely we can solve any philosophy problems, they are not inherently intractable.”

Briefly, I think both Nagel and McGinn are seriously mistaken — and I believe most philosophers agree, as testified by the straightforward observation that few seem to have stopped philosophizing as a result of considering these (well known) arguments.

Nagel has made a similar claim about the incompatibility of first and third person descriptions before, specifically in philosophy of mind (indeed, we will shortly discuss his classic paper on what it is like to be a bat). But that alleged incompatibility is more simply seen as two different types of descriptions of certain phenomena, descriptions that do not have to be incompatible, and yet that are not reducible to each other. Briefly, the fact that I feel pain (first person, subjective description) and that a neuroscientist will say that my C- fibers have fired (third person, objective description) are both true statements; they are compatible (indeed, I feel pain because my C-fibers are firing, as demonstrated by the fact that if I chemically inhibit that neurological mechanism I thereby cease to feel pain); and they are best understood, respectively, as an experience vs an explanation. But experiences don’t (have to) contradict explanations, assuming that the latter are at the least approximately true. A fortiori, I would like to see a good example of a philosophical problem that necessarily leads to incompatible treatments when tackled from either perspective. I do not think such a thing exists.

McGinn’s position is, quite simply, empty. While the analogy between the advanced understanding of an alien race vs our own primitive capacities and the similar difference between how dogs and humans understand English may seem compelling, there is no independent reason to think that philosophical problems are intractable by the human mind. Indeed, they have been tackled over the course of centuries, and we will see that progress has been made (once we understand “progress” in the way sketched above and to be further unpacked throughout the book). Interestingly, McGinn too, like Nagel before him, applies his approach to philosophy of mind, where he claims that the problem of consciousness cannot be resolved because we are just not smart enough. This “mysterian” position, as it is known, may be correct for all I know, but it doesn’t seem to lead us anywhere.

Similarly, where does Dietrich’s contemptuous rejection of the very idea of philosophical progress lead him? Nowhere, as far as I can see. He concludes by quoting Wittgenstein from the Tractatus: “My propositions are elucidatory in this way: he who understands me finally recognizes them as senseless, when he has climbed out through them, on them, over them. (He must so to speak throw away the ladder, after he has climbed up on it.) What we cannot speak about we must pass over in silence.” And yet, again, philosophy has persisted in existing as a field (I would be so bold as say, in moving forward!) despite Wittgenstein, and I greatly suspect will do much the same despite Dietrich’s cynicism.

A few comments now on Chalmer’s (2015) contribution to the question of progress, or lack thereof, in philosophy. He stakes a reasonable intermediate position, acknowledging that philosophy clearly has made progress, but asking why it hasn’t achieved more. He arrives at the first conclusion by a number of ways, including noting the incontrovertible fact that, for instance, the works of highly notable philosophers like Plato, Aristotle, Hume, Kant, Frege, Russell, Kripke, and Lewis have clearly been progressive with respect to the thinkers that preceded them, no matter what one’s conception of “progress” happens to be. Chalmers goes on to briefly discuss a number of way in which philosophy has, in fact, made progress: there has been convergence on some of the big questions (e.g., most professional philosophers are atheists and physicalists about mind), as well as some of the smaller ones (e.g., knowledge is not simply justified true belief, conditional probabilities are not probabilities of conditionals).

Still, maintains Chalmers, the progress that philosophy has made is slow and small in comparison to that of the natural (but not, he argues, the social) sciences. He discusses some possible explanations for this difference between philosophy and science, including: “disciplinary speciation,” the fact that new disciplines spin off philosophy precisely when they do begin to make sustained progress, like physics, psychology, economics, linguistics, and so on; “anti-realism,” the idea that certain areas of philosophy do not converge on truth because there is no such truth to be found (e.g., moral philosophy); “verbal disputes,” the Wittgensteinian point that at the least some debates in philosophy are more about using language at cross-purposes than about substantive differences (e.g., free will); “greater distance from the data,” meaning that for some reasons philosophy operates nearer the periphery of Quine’s famous web of beliefs (more on this in the next chapters); “sociological explanations,” where some positions become dominant, or recede in the background, because of the influence of individual philosophers within a given generation (e.g., the unpopularity of the analytic-synthetic distinction during Quine’s active academic career); “psychological explanations,” in the sense that individual philosophers may be more or less prone to endorse certain positions as a result of their character and other psychological traits; and “evolutionary explanations,” the contention that perhaps our naturally evolved minds are smart enough to pose philosophical questions but not to answer them.

Chalmers’ conclusion is that there may be some degree of truth to all seven explanations, but that they do not provide the full picture, in part because some of them apply to other fields as well: it’s not like natural scientists don’t have their own sociological and psychological quirks to deal with, and we may not be smart enough to settle philosophical questions, but we do seem smart enough to develop quantum mechanics and to solve Fermat’s Last Theorem. I think he is mostly on target, but I also think that the missing part of the explanation in his analysis derives from a crucial assumption that he made and that I will reject throughout this book: philosophy is simply not in the same sort of business as the natural sciences, so any talk of direct comparison in terms of progress and truths at the least partially misses the point. Right at the beginning of his paper Chalmers states: “The measure of progress I will use is collective convergence to the truth. The benchmark I will use is comparison to the hard sciences.” This is precisely what I will not do here, though it will take a bit to articulate and defend why.

A final parting note, in the spirit of Introductions as reading keys to one’s book. Friends and reviewers have of course commented on what you are about to read. Some of them found me too critical of, say, the continental approach to philosophy. Others, predictably, found me not critical enough. Some people thought parts of the book are too difficult for a generally educated reader (true), while other people thought some parts would be too obvious to a professional philosopher (also true). This was by design: I am writing with multiple audiences in mind, and I never believed one has to get one hundred percent of the references or arguments in a book in order to enjoy or learn from it (try to read the above quoted Wittgenstein that way and see how far you get, even as a professional philosopher — and there are much more blatant examples available). And of course the complaint has reasonably been raised that I don’t go into the proper degree of depth on a number of important technical issues in philosophy of science, of mathematics, of logic, and of philosophy itself (i.e., in meta-philosophy). Again, true. But what you are about to read is not meant as, nor could it possibly be, either an encyclopedia on philosophical thought or a set of simultaneous original contributions to many of the sub-specialties and specific issues I touch on. Rather, the goal is to pull together, the best I can, what a number of excellent thinkers have said on a variety of issues, connecting them into an overarching narrative that can provide a preliminary, organic stab at the question at the core of the book: does philosophy make progress, and if so, in which sense? I hope that that is justification enough for what you are about to read. And I am confident that better thinkers than I will soon make further progress down this road.

There are, of course, a number of people to whom I am grateful, either for reading drafts of this book (in toto or in part), or for having influenced what I am trying to do here as a result of our discussions. Among these are some of my colleagues at the City University of New York’s Graduate Center, particularly Graham Priest (for discussions about the nature of logic), Jesse Prinz (for discussions about the nature of everything, but particularly science), and Roberto Godfrey-Smith (on the nature of science and specifically biology). Leonard Finkleman is one of those who have read the book in its entirety, an effort for which I will be forever grateful. Thanks also to Dan Tippens for specific comments on two chapters (on progress in mathematics & logic, and in philosophy). Elizabeth Branch Dyson, at Chicago Press, has been immensely patient with my revisions of the original manuscript, not to mention as encouraging as an editor could possibly be (and has kindly agreed to finally publish the whole shebang in the form you are reading). I would also like to thank Patricia Churchland and Elliot Sober for the initial support when this project was at the stage of a proposal, as well as two anonymous reviewers for their severe, but obviously well intentioned, criticisms of previous drafts.

—Massimo Pigliucci
New York, Summer 2016

1. Philosophy’s PR Problem

“Philosophy is dead.”
(Stephen Hawking)

However one characterizes the discipline of philosophy, there is little doubt that it has been suffering for a while from a severe public relation problem, and it is incumbent on all interested parties (beginning with professionals in the field) not just to ask themselves why, but also what can be done to improve the situation. This chapter is offered as a series of reflections on these two aspects of the issue. We will examine in some detail a series of representative examples of brash attacks on philosophy (to which I will offer my own, shall we say, blunt response), mostly carried out by a small but influential number of scientists and science writers, attacks that seem to capture something fundamental about the broader public’s attitude toward the discipline. As a scientist myself, I think I am unusually positioned to understand some of my colleagues’ take on philosophy. We will also see, however, that there is a number of prominent philosophers who have had the unfortunate effect of contributing to the problem by writing questionable things about science, thus somewhat justifying the backlash from the other side. Finally, we will look at how — despite the obliviousness of, and sometimes even objections and resistance by, most professional philosophers — the field has been making significant inroads in public discourse, ironically by essentially following the example set forth by science popularizing.

(Some) Scientists against philosophers

Science, as is well understood, is one of philosophy’s intellectual offsprings, and was in fact known until the mid-19th century as “natural philosophy.” The very word “scientist” was invented in 1833 by philosopher William Whewell, apparently at the prompting of the poet Samuel Taylor Coleridge (Snyder 2006). There are very good historical and conceptual reasons for the weaning to have occurred (Bowler and Morus, 2005; Lindberg 2008), a process that eventually led to the professionalization of academic science, which dramatically accelerated after World War II with the establishment (in the United States and elsewhere) of government sources of funding for scientific research. Given that the separation of the two fields has occurred slowly and — initially at least — amicably (both Descartes and Newton, for instance, considered themselves natural philosophers), one would expect each side to eventually go on with their business and leave the other to pursue its own. The reality is a bit more complicated than that.

As we shall see in a couple of chapters, some philosophers, especially analytical ones, do seem to suffer from a degree of “lab coat envy,” so to speak, which nudges them to concede perhaps a bit too much epistemic territory to science. At the opposite extreme, we have also had episodes of philosophers lashing out at science, often for egregiously bad reasons, thereby generating a (frequently scornful) reaction from the scientists themselves. It seems therefore appropriate to begin with an examination of what some vocal and prominent exponents of modern day natural philosophy have had to say recently about their mother discipline, and why they have so frequently and reliably missed the mark. Be forewarned: going through this section will increasingly feel like seeing some dirty intellectual laundry being aired in public. But I think it is a necessary preamble to my argument, and at any rate the pronouncements I will focus on and criticize below are already out there for anyone to see and make up their own mind about.

A good starting point, which I will discuss in detail since it is so paradigmatic, is a famous essay by Nobel winning physicist Steven Weinberg, boldly entitled “Against Philosophy” (Weinberg 1994). The question Weinberg poses right at the end of the first paragraph of his essay, “Can philosophy give us any guidance toward a final theory?” is at once typical of physicists’ complaints about the discipline, and clearly shows why they are misguided. While there are a number of good examples of fruitful collaborations between scientists and philosophers, from evolutionary biology to quantum theory, the major point of philosophy of science (Weinberg's main target) is most emphatically not to solve scientific (i.e., empirical) questions. We’ve got science for that, and it works very nicely.

Weinberg immediately tries to take some of the sting out of his overture by acknowledging the general value of philosophy, “much of which has nothing to do with science,” but immediately springs back to slinging mud within the same paragraph: “philosophy of science, at its best seems to me a pleasing gloss on the history and discoveries of science.” There are various aims of philosophy of science (Pigliucci 2008), only some of which have to do with helping physicists formulate new theories about the ultimate structure of the universe (or biologists to formulate new theories of evolution, and so on). Broadly speaking, philosophers of science are interested in three major areas of inquiry. The first deals with the generation of general theories of how science works, as in Popper’s (1963) ideas about falsificationism, or Kuhn’s (1963) concept of scientific revolutions and paradigm shifts. Second, philosophers of particular sciences (such as physics, biology, chemistry, etc.) are interested in the logic underlying the practice of the various subdivisions of the scientific enterprise, debating the use (and sometimes misuse) of concepts such as those of species (in biology: Wilkins 2009) or wave function (in physics: Krips 1990). Finally, philosophy of science may serve as an external mediator and sometimes critic of the social implications of scientific findings, as for instance in the case of the complex evidential and ethical issues raised by human genetic research (Kaplan 2000). While some of the above should be useful to working scientists, most of it is an exercising in studying science from the outside, not of practicing science itself, thus making Weinberg’s demand for direct help from philosophers in theoretical physics rather odd.

It is also not difficult to find outright misreadings of the philosophical literature in “Against Philosophy.” For instance, at one point Weinberg cites Wittgenstein in support of his thesis that philosophy is irrelevant to science: “Wittgenstein remarked that ‘nothing seems to me less likely than that a scientist or mathematician who reads me should be seriously influenced in the way he works.’” But this should be read in context (admittedly, not an easy task, when it comes to Wittgenstein), as the author was actually making an argument for the independence of philosophy from science and for the simultaneous deflating of the latter, and was definitely not talking about philosophy of science. Weinberg then comes perilously close to anti-intellectualism when he complains that, after reading some philosophy “from time to time,” he finds “some of it ... to be written in a jargon so impenetrable that I can only think that it aimed at impressing those who confound obscurity with profundity.” I’m confident that precisely the same unwarranted judgment could be made about any paper in fundamental physics, when read by someone who does not have the technical training necessary to read fundamental physics!

Weinberg complains about the fact that when he gives talks about the Big Bang someone in the audience regularly poses a “philosophical” question about the necessity of something existing before that moment, even though physics tells us that time itself started with the Big Bang, which means that the question of what was there before that pivotal event is meaningless. But a Nobel winner ought to understand the difference between a random member of the audience at a popular talk and the thinking of professional philosophers of physics. Indeed, Weinberg himself gives some credit to philosophers past when he points out that Augustine (in the 4th century, nonetheless) explicitly considered the same problem and “came to the conclusion that it is wrong to ask what there was before God created the universe, because God, who is outside time, created time along with the universe.” So, philosophers do get some things right after all, in this case a full millennium and a half before physicists.

It is interesting that Weinberg attempts to show how philosophy (of science) occasionally does help science itself, but only insofar as it frees scientists from other, bad, philosophy. His examples are illuminating as to where at least part of the problem with his analysis resides. He mentions, for instance, that logical positivism — a philosophical position that was current in the early part of the 20th century — “helped to free Einstein from the notion that there is an absolute sense to a statement that two events are simultaneous; he found that no measurement could provide a criterion for simultaneity that would give the same result for all observers. This concern with what can actually be observed is the essence of positivism.” Moreover, again according to Weinberg, positivism played a constructive role in the beginning of quantum mechanics: “The uncertainty principle, which is one of the foundations of the probabilistic interpretation of quantum mechanics, is based on Heisenberg’s positivistic analysis of the limitations we encounter when we set out to observe a particle’s position and momentum.”

But Weinberg then complains that the “aura” of positivism outlasted its value, and that its philosophical framework began to hinder research in fundamental physics. He endorses George Gale’s opinion that positivism is likely to blame for the current negative relationship between philosophers and physicists, going on to list examples of alleged damage, such as the resistance to atomism and the resulting delayed acceptance of statistical mechanics, as well as the late acceptance of the wave function as a physical reality. But even assuming that Weinberg’s take on the history of science is correct (after all, he is relying on anecdotal evidence, not on a professional, systematic historical analysis), there is a basic fallacy underlying his reasoning. He is imagining a static model of philosophy, whereby views do not change — much less progress — over time. But why should that be? Why is it acceptable that science abandons, say, Newtonian mechanics in favor of relativity theory, while philosophy cannot abandon logical positivism in favor of more sophisticated notions? Indeed, this is precisely what happened (Ladyman 2012). It is simply historically incorrect to claim that positivism may underlie the current disagreements between philosophers and physicists, because philosophers have not considered logical positivism a viable notion in philosophy of science since at the least the middle part of the 20th century, following the devastating critiques of Popper and others in the 1930s, and ending with those of Quine, Putnam and Kuhn in the 1960s.. If physicists still think that positivism commands the field in philosophy then it is the physicists who need to update their notions of where philosophy is. When Weinberg states that “it seems to me unlikely that the positivist attitude will be of much help in the future” he is absolutely right, but no philosopher of science would dispute that — or has done so for a number of decades.

At this point in Weinberg’s essay there is what appears to be a seamless transition, but is instead a logical gap that reveals much about some scientists’ misconceptions regarding philosophy. After having dispatched logical positivism, the author turns to attack “philosophical relativists,” by which he likely means some of the most extreme postmodernist and deconstructionist authors that played a role in the so-called “science wars” of the 1990s (Sokal and Bricmont 2003). I will tackle this particular episode in more detail below and then again in the next chapter, but it is worth remarking here that scientists such as physicist Alan Sokal have been joined en force in rebutting epistemic relativism by a number of philosophers, mostly, in fact, philosophers of science. What Weinberg does not appreciate is that philosophers of science are typically highly respectful of science and do come to its defense whenever this is needed (other classic examples include the debate over Intelligent Design (Pennock 1998) and discussions about pseudoscience (Pigliucci and Boudry 2013)).

Indeed, Weinberg himself could use some philosophical pointers when he struggles against the postmodern charge that science does not make progress. He says: “I cannot prove that science is like this [making progress], but everything in my experience as a scientist convinces me that it is. The ‘negotiations’ over changes in scientific theory go on and on, with scientists changing their minds again and again in response to calculations and experiments, until finally one view or another bears an unmistakable mark of objective success. It certainly feels to me that we are discovering something real in physics, something that is what it is without any regard to the social or historical conditions that allowed us to discover it.” What Weinberg cannot prove, what he has to resort to his gut feelings to argue for, is the bread and butter of the realism-antirealism debate in philosophy of science, to which we will turn in some depth later on, as one of the best illustrations of the idea underlying this book, that philosophy makes progress.

The second example of a scientist who misunderstands philosophy that I wish to discuss in order to build my case is another physicist, Lawrence Krauss. He first presented his thoughts on the matter in an interview with The Atlantic magazine conducted by journalist Ross Andersen (Andersen 2012). To put things in context, the discussion took off with a reference to Krauss’ book on cosmology for the general public, A Universe from Nothing: Why There is Something Rather Than Nothing, in which Krauss maintains that science has all but solved the old (philosophical) question of why there is a universe in the first place. The book was much praised shortly after publication, but later had been harshly criticized by David Albert in the New York Times. Here is Albert (2012) summarizing the gist of his criticism of Krauss, that the physicist played a bait and switch with his readers, substituting quantum fields for the “nothing” of the book’s title:

“The particular, eternally persisting, elementary physical stuff of the world, according to the standard presentations of relativistic quantum field theories, consists (unsurprisingly) of relativistic quantum fields ... They have nothing whatsoever to say on the subject of where those fields came from, or of why the world should have consisted of the particular kinds of fields it does, or of why it should have consisted of fields at all, or of why there should have been a world in the first place. Period. Case closed. End of story.”

That’s harsh, as much as I think it is on target, and Krauss understandably didn’t like Albert’s review. Still, I wonder if Krauss was justified in referring to Albert as a “moronic philosopher,” considering that the latter is not only a highly respected philosopher of physics at Columbia University, but also holds a PhD in theoretical physics. I didn’t think Rockefeller University (where Albert got his degree) gave out PhD’s to morons, but I could be wrong.

Nonetheless, let’s get to the core of Krauss’ attack on philosophy. He said: “Every time there’s a leap in physics, it encroaches on these areas that philosophers have carefully sequestered away to themselves, and so then you have this natural resentment on the part of philosophers.” This seems to show a couple of things: first, that Krauss does not appear to genuinely care to understand what the business of philosophy (especially philosophy of science) is, or he would have tried a bit harder; second, that he doesn’t mind playing armchair psychologist, despite the dearth of evidence for his pop psychological “explanation” of why philosophers allegedly do what they do.

Here is another gem: “Philosophy is a field that, unfortunately, reminds me of that old Woody Allen joke, ‘those that can’t do, teach; and those that can’t teach, teach gym.’ And the worst part of philosophy is the philosophy of science; the only people, as far as I can tell, that read work by philosophers of science are other philosophers of science. It has no impact on physics what so ever. ... They have every right to feel threatened, because science progresses and philosophy doesn’t.”

In response to which, I think, it would be fair to point out that the only people who read works in theoretical physics are theoretical physicists. More seriously, once again, the major aim of philosophy (of science, in particular) is not to solve scientific problems. To see how strange Krauss’ complaint is just think of what it would sound like if he had said that historians of physics haven’t solved a single puzzle in theoretical physics. That’s because historians do history, not science. And the reader will have noticed the jab at philosophy for not making progress, which is the underlying reason to discuss these statements in the present volume to begin with.

Andersen, at this point in the interview, must have been a bit fed up with Krauss’ ego, so he pointed out that actually philosophers have contributed to a number of science or science-related fields, and mentioned computer science and its intimate connection with logic. He even named Bertrand Russell as a pivotal figure in this context. Ah, responded Krauss, but really, logic is a branch of mathematics, so philosophy doesn’t get credit. And at any rate, Russell was a mathematician, according to Krauss, so he doesn’t count either. The cosmologist goes on to claim that Wittgenstein was “very mathematical,” as if it were somehow surprising to find philosophers who are conversant in logic and math.

Andersen, however, wasn’t moved and insisted: “Certainly philosophers like John Rawls have been immensely influential in fields like political science and public policy. Do you view those as legitimate achievements?” And here Krauss was forced to deliver one of the lamest responses I can recall in a long time: “Well, yeah, I mean, look I was being provocative, as I tend to do every now and then in order to get people’s attention.” This is a rather odd admission from someone who later on in the same interview claims that “if you’re writing for the public, the one thing you can’t do is overstate your claim, because people are going to believe you.”

Krauss also has a naively optimistic view of the business of science, as it turns out. For instance, he claims that “the difference [between scientists and philosophers] is that scientists are really happy when they get it wrong, because it means that there’s more to learn.” I’ve practiced science for a quarter century, and I’ve never seen anyone happy to be shown wrong, or who didn’t react as defensively (or even offensively) as possible to any suggestion that he might be wrong. Indeed, as physicist Max Plank famously put it, “science progresses funeral by funeral,” because often the old generation has to retire and die before new ideas really take hold. Scientists are just human beings, and like all human beings they are interested in mundane things like sex, fame and money (and yes, the pursuit of knowledge). Science is a wonderful and wonderfully successful activity, but there is no reason to try to make its practitioners into some species of intellectual saints that they certainly are not.

Finally, on the issue of whether Albert the “moronic” theoretical physicist-philosopher has a point in criticizing Krauss’ book, Andersen remarked: “It sounds like you’re arguing that ‘nothing’ is really a quantum vacuum, and that a quantum vacuum is unstable in such a way as to make the production of matter and space inevitable. But a quantum vacuum has properties. For one, it is subject to the equations of quantum field theory. Why should we think of it as nothing?” To which Krauss replied by engaging in what looks to me like a bit of handwaving: “I don’t think I argued that physics has definitively shown how something could come from nothing; physics has shown how plausible physical mechanisms might cause this to happen. ... I don’t really give a damn about what ‘nothing’ means to philosophers; I care about the ‘nothing’ of reality. And if the ‘nothing’ of reality is full of stuff, then I’ll go with that.” A nothing full of stuff? No wonder Albert wasn’t convinced.

But, insisted Andersen, “when I read the title of your book, I read it as ‘questions about origins are over.’” To which Krauss responded: “Well, if that hook gets you into the book that’s great. But in all seriousness, I never make that claim. ... If I’d just titled the book ‘A Marvelous Universe,’ not as many people would have been attracted to it.” Again, this from someone who had just lectured readers about honesty in communicating with the public. I think my case about Krauss can rest here, though interested readers are invited to check his half-hearted “apology” stemming from his exchange with Andersen and published in Scientific American (Krauss 2012), or is equally revealing interview in The Guardian with philosopher Julian Baggini (Baggini and Krauss 2012).

I do not wish to leave the reader with the impression that only some physicists display a dyspeptic reaction toward philosophy, a few life scientists do it too. Perhaps my favorite example is writer Sam Harris (2011), who — on the strength of his graduate research in neurobiology — wrote a provocative book entitled The Moral Landscape: How Science Can Determine Human Values. What Harris set out to do in that book was nothing less than to mount a science-based challenge to Hume’s classic separation of facts from values. For Harris, values are facts, and as such they are amenable to scientific inquiry.

Before I get to the meat, let me point out that I think Harris undermines his own project in two endnotes tucked in at the back of his book. In the second note to the Introduction, he acknowledges that he “do[es] not intend to make a hard distinction between ‘science’ and other intellectual contexts in which we discuss ‘facts.’” But if that is the case, if we can define “science” as any type of rational-empirical inquiry into “facts” (the scare quotes are his) then we are talking about something that is not at all what most readers are likely to understand when they pick up a book with a subtitle that says “How Science Can Determine Human Values.” One can reasonably smell a bait and switch here. Second, in the first footnote to chapter 1, Harris says: “Many of my critics fault me for not engaging more directly with the academic literature on moral philosophy ... [But] I am convinced that every appearance of terms like ‘metaethics,’ ‘deontology,’ ... directly increases the amount of boredom in the universe.” In other words, the whole of the only field other than religion that has ever dealt with ethics is dismissed by Sam Harris because he finds its terminology boring. Is that a fact or a value judgment, I wonder?

Broadly speaking, Harris wants to deliver moral decision making to science because he wants to defeat the evil (if oddly paired) twins of religious fanaticism and moral relativism. Despite the fact that I think he grossly overestimates the pervasiveness of the latter, we are together on this. Except of course that the best arguments against both positions are philosophical, not scientific. For instance, the most convincing reason why gods cannot possibly have anything to do with morality was presented 24 centuries ago by Plato (circa 399BCE / 2012), in his Euthyphro dialogue (which goes, predictably, entirely unmentioned in The Moral Landscape). In the dialogue, Socrates asks a young man named Euthyphro the following question: “The point which I should first wish to understand is whether the pious or holy is beloved by the gods because it is holy, or holy because it is beloved of the gods?” That is, does God embrace moral principles naturally occurring and external to Him because they are sound (“holy”) or are these moral principles sound because He endorses them? It cannot be both, and the choice is not pretty, since the two horns lead to either a concept of (divine, in this instance) might makes right or to the conclusion that moral principles are independent of gods, which means we can potentially access them without the intermediacy of the divine. As for moral relativism, it has been the focus of sustained and devastating attacks in philosophy, for instance by thinkers such as Peter Singer and Simon Blackburn, but of course in order to be aware of that one would have to read precisely the kind of metaethical literature that Harris finds so increases the degree of boredom in the universe.

Ultimately, Harris really wants science — and particularly neuroscience (which just happens to be his own specialty) — to help us out of our moral quandaries. Except that the reader will await in vain throughout the book to find a single example of new moral insights that science provides us with. For instance, Harris tells us that genital mutilation of young girls is wrong. I agree, but certainly we have no need of fMRI scans to tell us why: the fact that certain specific regions of the brain are involved in pain and suffering, and that we might be able to measure exactly the intensity of those emotions doesn’t add anything at all to the conclusion that genital mutilation is wrong because it violates an individual’s right to physical integrity and to avoid pain unless absolutely necessary (e.g., during a surgical operation to save her life, if no anesthetic is available).

Indeed, Harris’ insistence on neurobiology becomes at times positively creepy (a sure mark of scientism since at the least the eugenic era: Adams 1990), as in the section where he seems to relish the prospect of a neuro-scanning technology that will be able to tell us if anyone is lying, opening the prospect of a world where government (and corporations) will be able to enforce “no-lie zones” upon us. He writes: “Thereafter, civilized men and women might share a common presumption: that whenever important conversations are held, the truthfulness of all participants will be monitored. ... Many of us might no more feel deprived of the freedom to lie during a job interview or at a press conference than we currently feel deprived of the freedom to remove our pants in the supermarket.” I don’t know about you, but for me these sentences conjure the specter of a really, really scary Big Brother, which I most definitely would rather avoid, science be damned (on the dangers of too much utilitarianism, see: Thomas et al. 2011).

At several points in the book Harris seems to think that neurobiology will be so important for ethics that we will be able to tell whether people are happy by scanning them and make sure their pleasure centers are activated. He goes so far as arguing that scientific research shows that we are wrong about what makes us happy, and that it is conceivable that “evil” (quite a metaphysically loaded term, for a book that shies away from philosophy) might turn out to be one of many paths to happiness — meaning the stimulation of certain neural pathways in our brains. Besides the obvious point that if what we want to do is stimulate our brains so that we feel perennially “happy” then all we need are appropriate drugs to be injected into our veins while we sit in a pod in perfectly imbecilic contentment (see Nozick’s (1974, 644-646) famous experience machine thought experiment), these are all excellent observations that ironically deny that science, by itself, can answer moral questions. As Harris points out, for instance, research shows that people become less happy when they have children. What does this scientific fact about human behavior have to do with ethical decisions concerning whether and when to have children? [4]

Moreover, as we saw, Harris entirely evades philosophical criticism of his positions on the simple ground that he finds metaethics “boring.” But he is a self-professed consequentialist who simply ducks any discussion of the implications of that a priori choice of ethical framework, a choice that informs his entire view of what counts for morality, happiness, well-being and so forth. He seems unaware of (or doesn’t care about) the serious philosophical objections that have been raised against consequentialism, and even less so of the various counter-moves in conceptual space that consequentialists have made to defend their position (we will explore some of this territory). This ignorance is not bliss, and it is the high price Harris’ readers pay for the crucial evasive maneuvers that the author sneaks into the initial footnotes I mentioned above.

Now, what are we to make of all of the above? I am not particularly interested in simply showing how philosophically naive Weinberg, Krauss, Harris or several others (the list is surprisingly long, and getting longer) are, as much fun as that sometimes is. Rather, I want to ask the broader question of what underlies these scientists’ take on science and philosophy. I think it is fair to say that the above criticisms of philosophy are built on the following implicit argument:

Premise 1: Empirical evidence is the province of science (and only science).

Premise 2: All meaningful / answerable questions are by nature empirical.

Premise 3: Philosophy does not deal with empirical questions.

Conclusion: Therefore, science is the only activity that provides meaningful / answerable questions.

Corollary: Philosophy is useless.

Now, P2 is awfully close to the philosophical (!) position known as logical positivism, which as I mentioned has been demolished by the likes of Quine, Putnam, Kuhn and others (and which, you may recall, Weinberg himself clearly didn’t like). I have already pointed out that there are plenty of questions whose nature is not empirical, or not wholly empirical, and yet that are meaningful. P3 can be interpreted in more than one way: yes, philosophy isn’t in the business of answering empirical questions (just like mathematics and logic), but it is a caricature of the field to claim that empirical facts are irrelevant to philosophical considerations, and no sane philosopher would defend such claim.

This would already be enough to show that both the Conclusion and the Corollary do not follow, and we could go home with the satisfaction of a job well done. But I want to add something about P1. This appears to be the assumption of some prominent scientists, manifested most clearly in biologist Jerry Coyne’s argument that plumbing is for all effective purposes a science because it deals with empirical evidence, which plumbers use to evaluate alternative “hypotheses” concerning the causal mechanism underlying your toilette’s clog. There is a fallacy of equivocation at work here, as the word “science” should be used in one of two possible meanings, but not both: either Krauss, Coyne et al. mean that (a) science is any human activity that uses facts to reach conclusions; or they mean that (b) science is a particular type of social activity, historically developed, and characterized by things like peer review, granting agencies, complex instrumentation, sophisticated analytical tools etc. (Longino 1990, 2006).

(b) is what most people — including most scientists — mean when they use the word “science,” and by that standard plumbing is not a science. More importantly, philosophy then can reasonably help itself to facts and still maintain a degree of independence (in subject matter and methods) from science. If we go with (a) instead, it would follow not only that plumbers are scientists, but also that I am doing “science” every time I pick the subway route that brings me somewhere in Manhattan. After all, I am evaluating hypotheses (the #6 train will let me get to 86th Street at the corner with Lexington) based on my theoretical understanding of the problem (the subway map), and the available empirical evidence (the directly observable positions of the stations with respect to the Manhattan street grid, and so on). You can see, I hope, that this exercise quickly becomes silly and as a consequence the word “science” loses meaning. Why would we want that?

Why is this happening?

We now need to explore the reasons for this bizarre internecine wars between the two disciplines if we wish to move on to more fertile pursuits. As it happens, there are, I think, a number of potentially good explanations for the sorry state of affairs of which the above was a sample. Moreover, these explanations immediately suggest actionable items that both scientists and philosophers should seriously consider.

There are three recurring themes in the science-philosophy quarrels when seen from the point of view of the scientists involved, themes that we have encountered when examining Weinberg, Krauss and Harris’ writings. The three themes are:

(i) A degree of ignorance of philosophy, and even often of the history of science.

(ii) Fear of epistemic relativism, which is seen as undermining the special status of science.

(iii) A (justifiable) reaction to (some) prominent philosophers’ questionable writings about science.

Let’s begin with (i). While clearly an appreciation of the history and philosophy of science is not a requirement to obtain a PhD in the natural sciences (whether it should be is a different issue to be set aside for another day, but see for instance, Casadevall 2015), it is not difficult to find scientists who are conversant in those allied disciplines. The degree to which this is true varies with discipline, time, and even cultural setting. For instance, physicists have historically been more sensitive than other scientists to philosophical issues, but in recent decades the explosive growth of the philosophy of biology has prompted a number of biologists to initiate fruitful collaborations with philosophers to address issues such as species concepts (Lawton 1999; Pigliucci 2003), whether there are laws in ecology (Wilkins 2009), and others.

However, physicist Lee Smolin (2007), in his The Trouble with Physics laments what he calls the loss of a generation for theoretical physics, the first one since the late 19th century to pass without a major theoretical breakthrough that has been empirically verified. Smolin blames this problematic state of affairs on a variety of factors, including the complex sociology of a discipline where funding and hiring priorities are set by a small number of intellectually inbred practitioners. Interestingly, one of Smolin’s suggested culprits for what he sees as the failures of contemporary fundamental physics is the dearth of interest in and appreciation of philosophy among physicists themselves. This quote, for instance, is by Einstein, cited in Smolin’s book:

“I fully agree with you about the significance and educational value of methodology as well as history and philosophy of science. So many people today — and even professional scientists — seem to me like someone who has seen thousands of trees but has never seen a forest. A knowledge of the historical and philosophical background gives that kind of independence from prejudices of his generation from which most scientists are suffering. This independence created by philosophical insight is — in my opinion — the mark of distinction between a mere artisan or specialist and a real seeker after truth.” (Albert Einstein)

This is certainly the proper territory of historical and sociological analysis, but there is enough prima facie evidence in the literature to suggest that a number of prominent scientists simply do not know what they are talking about when it comes to philosophy (and particularly philosophy of science). I am not sure how this could be remedied (other than through the unlikely imposition of mandatory courses in history and philosophy of science for budding scientists), but at the very least one could strongly suggest to our esteemed colleagues that they follow Wittgenstein’s famous advice (given, originally, in quite a different context): Whereof one cannot speak, thereof one must be silent.

Moving on to point (ii) above, it concerns the so-called “science wars” of the 1990s and early 21st century, Sokal affair and all included. There is no need to rehash the details of the arguments and counter-arguments here, as even books that purport to be fair and balanced (Labinger and Collins 2001) end up containing a sizable amount of what can only be characterized as sniping and counter-sniping. But — at the cost of some simplification — it may be useful to summarize the extreme positions as well as what should instead be agreed to by all sensible parties, in the hope of providing a reference baseline that can be used to argue in favor of a mutually agreeable cease fire.

On the one hand, the extreme postmodernist position (or, at least, the caricature of postmodernism that is lampooned by scientists like Sokal, Weinberg et al.) is the idea that science is largely or almost exclusively a social construction. Arguably the most infamous summary of this view is from Harry Collins (1981): “The natural world has a small or non- existent role in the construction of scientific knowledge.” When one actually checks the original paper, however, it is not entirely clear whether Collins himself endorses this view or whether he simply mentions that some scholars embrace a fully relativistic take on science (in the endnote to that quote Collins seems to think that sociologist of science David Bloor and some of his colleagues do). Be that as it may, that position — whether explicitly held by anyone, implied or hinted at — is nonsense on stilts. The natural world very much plays a large (though certainly not completely determining) role in the construction of scientific knowledge. On the other hand, the extreme scientific realist position is supposed to be that sociological and psychological factors have next to nothing to do with the actual practice of science, the latter being an activity essentially independent of culture. As Weinberg (2001) put it: “Even though a scientific theory is in a sense a social consensus, it is unlike any other sort of consensus in that it is culture-free and permanent.” But, again, read in context this strong statement by Weinberg is qualified by his acknowledgment that there are indeed components of scientific theories (which he calls “soft”) that are not, in fact, permanent, and moreover there are both psychological and sociological factors at play during the shaping of scientific theories. That said, no scientist should seriously hold to the idea that science is a purely data-driven enterprise relentlessly moving toward eternal objective truths, so that we can safely relegate that view also to the heap of fashionable nonsense.

What then? It seems obvious — but apparently needs to be stated explicitly — that a serious account of how science actually works will take on board the mounting scholarship in three distinct yet related fields: history, philosophy and sociology of science. To simplify quite a bit: history of science is in the business of reconstructing the actual historical paths taken by various scientific disciplines, their empirical discoveries, and their theoretical outputs; the aim of philosophy of science is to examine the logic and epistemic aspects of scientific practice, indicating both why it works (when it does) and why it may occasionally fail; and sociology of science is interested in the analysis of the social structure internal to the scientific community itself, to see how it shapes the way scientists think, how they determine their priorities and why entire fields move in certain directions that may be underdetermined by epistemic factors. Scientists are, of course, free to simply ignore the history, philosophy and sociology of their own discipline, as they can get along with their work just fine without them. But they are not free — on penalty of being charged with anti-intellectualism — to dismiss those very same areas of scholarship on specious ground, such as that they undermine the authority of science, or that they do not contribute to scientific progress.

Lastly, (iii) above is the area where, unfortunately, scientists do in fact have good reasons to complain. It is certainly the case that, from time to time, professional philosophers — indeed, highly visible luminaries of the field — engage in questionable and somewhat badly informed writing about science, ending up not helping the image of their own discipline. Two recent examples will suffice to make the point: Jerry Fodor and Thomas Nagel.

Fodor is best known as a philosopher of mind, and is indeed someone who has engaged very fruitfully during his long career with cognitive scientists. One of my favorite gems from his extensive collection of publications is the little booklet entitled The Mind Doesn’t Work That Way (2000), his critical response to Steven Pinker’s (1997) presentation of the computational theory of mind in How The Mind Works. However, more recently Fodor (2010) co-authored a book with cognitive scientist Massimo Piattelli-Palmarini, provocatively entitled What Darwin Got Wrong, and therein the trouble began (Pigliucci 2010; see also — among many others — reviews by: Block and Kitcher 2010; Coyne 2010; Godfrey-Smith 2010; Lewontin, 2010; Richards 2010).

My own take on their effort is that Fodor and Palmarini made a mess of what could have been an important contribution, largely by misusing philosophical distinctions and misinterpreting the literature on natural selection. They are correct in two of their assessments: it is the case that mainstream evolutionary biology has become complacent with the nearly 70-year-old Modern Synthesis, which reconciled the original theory of natural selection with Mendelian and population genetics; and it is true that the field may need to extend the conceptual arsenal of current evolutionary theory (Pigliucci and Müller 2010). But in claiming that there are fundamental flaws in an edifice that has withstood a century and a half of critical examination, they went horribly wrong.

Their argument against “Darwinism” boils down to a two-pronged attack. First, they assert that biologists’ emphasis on ecological, or exogenous, factors is misplaced because endogenous genetic and developmental constraints play a crucial part in generating organic forms. Second, they argue that natural selection cannot be an evolutionary mechanism because evolution is a historical process, and history is “just one damned thing after another” with no overarching logic.

The first claim is simply a distortion of the literature. The relative importance of natural selection and internal constraints has always been weighed by biologists: molecular and developmental biologists tend to focus on internal mechanisms; ecologists and evolutionary biologists prefer to address external ones. But even Darwin accepted the importance of both: in The Origin of Species, his “laws of variation” acknowledge that variation is constrained, and his “correlation of growth” implies that organismal traits are interdependent.

Fodor and Palmarini misappropriated the critique of adaptationism (the idea that natural selection is sufficient to explain every complex biological trait) that Stephen Jay Gould and Richard Lewontin presented in their famous “spandrels” paper of 1979. Gould and Lewontin warned about the dangers of invoking natural selection without considering alternatives. But Fodor and Palmarini grossly overstate that case, concluding that natural selection has little or no role in the generation of biological complexity, contrary to much accumulated evidence.

In their second line of attack, the authors maintain that biological phenomena are a matter of historical contingency. They argue that generalizations are impossible because of the interplay of too many local conditions, such as ecology, genetics and chance. In their narrow view of what counts as science, only law-like processes allow for the testability of scientific hypotheses. Thus, they claim, an explanation of adaptations that is based on natural selection is defensible in only two cases — if there is intelligent design, or if there are laws of biology analogous to those of physics, both of which they (rightly) reject. Fodor and Palmarini ignore the entire field of evolutionary ecology, countless examples of convergent evolution of similar structures in different lineages that show the historical predictability of evolutionary processes, and the literature on experimental evolution, in which similar conditions consistently yield similar outcomes. There clearly is a logic to evolution, albeit not a Newtonian one.

Evolutionary biology is a mix of chance and necessity, as French biologist Jacques Monod famously put it, in which endogenous and exogenous factors are in constant interplay. It is a fertile area for rigorous philosophical analysis. But Fodor and Palmarini passed a good chance to contribute to an important discussion at the interface between philosophy and science, ending up instead by offering a sterile and wrongheaded criticism. This is unfortunately the very sort of thing that evolutionary biologists can legitimately complain about and lay at the feet of philosophy — and they have, vociferously.

The second example concerns Thomas Nagel, another philosopher of mind, perhaps most famous for the highly influential and beautifully written “What is it like to be a bat?” (1974), in which he argues that science is simply not in the business of accounting for first person phenomenal experiences (“qualia”). But even Nagel couldn’t resist the anti- Darwinian temptation, as is evident from his Mind and Cosmos (2012). Unlike Fodor’s relatively narrowly focused attack on the biological theory of evolution per se, Nagel’s broadside is against what he characterizes as the “materialist neo-Darwinian conception of nature,” as the subtitle of the book clearly advertises. The problem is that it is hard to see who, exactly, holds to such conception, or what, precisely, this conception consists of. Nagel, for one, doesn’t say much about it, frankly admitting that a great deal of what he is reacting to can be found in popular (i.e., non-technical) accounts of science or the philosophy of science. (Again, plenty of detailed reviews available, including: Dupré 2012; Leiter and Weisberg 2012; Carroll 2013; Godfrey-Smith 2013; Orr 2013.)

Nagel appears to aim at two targets: the sort of theoretical reductionism advocated by physicists like Steven Weinberg, and the kind of Darwin-inspired naturalism defended by Dan Dennett. But Weinberg’s reductionism has precisely nothing to do with Darwinism, “neo-” or not, and it is arguable that Dennett (1996) — who does think of “Darwinism” as a “universal acid” corroding some of our most cherished beliefs about reality — would agree with Nagel’s characterization of his own position.

Concerning the first target, it is noteworthy that — as Leiter and Weisberg (2012) point out in their review of Nagel’s book — most philosophers do in fact reject the kind of crude theoretical reductionism that Nagel is so worked up about. (That said, perhaps it is the case that many scientists hold to that sort of reductionism, and/or that it is beginning to permeate popular perceptions of science. But these are claims that one would think need to be heavily substantiated before one launches into their debunking.)

Nagel’s second attack, against naturalism, is more interesting, but also seriously flawed. His two basic objections to what he calls “neo-Darwinian” naturalism are that: (a) it is counter-intuitive to common sense; and (b) there are examples of objective truths that cannot be explained by the theory of evolution. The only sensible reaction to (a) is a resounding “so what?” Much of science (and philosophy) runs counter to commonsense, but that has never provided a particularly good reason to reject it. (b) is more intriguing, but Nagel’s defense of it is ineffective. His two examples of objective truths that escape the explanatory power of neo-Darwinism are moral and mathematical truths. I actually agree, but it is not clear what this will purchase. To begin with, there are several accounts of ethics that are not based on the idea that moral truths are objective in any strong, mind- independent sense of the term (Campbell 2011). I, for one, think that ethics is a type of reasoning about the human condition, not a set of universal truths. One begins with a number of assumptions (about values, about facts concerning human nature) and derives their logical consequences, with things getting interesting whenever different assumptions (about values, for instance) inevitably come into conflict with each other. Of course, much more can be said about meta-ethics and ethical realism, but I have to refer the reader to the several excellent reviews of Nagel’s book listed above.

Nagel’s point about mathematical truths is interesting, as a number of mathematicians and philosophers of mathematics do lean toward a naturalistic version of mathematical Platonism (but see my rejection of it for the purposes of this book in the Introduction), and there are serious arguments in its favor (Brown 2008; Linnebo 2011). But the claim that natural selection cannot possibly explain how we can “grasp” mathematical truths is rather simplistic. Not only is natural selection not the only explanatory principle in evolutionary biology. It, for instance, likely cannot explain the variety of human languages either, without this implying that the existence of complex and multiple idioms somehow is a blow to evolutionary theory, to naturalism or whatever. It is also easy to imagine alternative explanations for our mathematical capacities, such as that a rudimentary ability to entertain abstract objects and engage in arithmetics was indeed of value to our ancestors, but that it is cultural evolution that is primarily responsible for having built on those flimsy basis to the point of allowing (some, very few of) us to, say, solve Fermat’s Last Theorem.

The point is that, when Nagel builds a very tentative edifice, from which he then launches into bold claims such as “in addition to physical law of the familiar kind, there are other laws of nature that are ‘biased toward the marvelous,’” one could see why scientists (and other philosophers) begin to roll their eyes and walk away from the whole darn thing in frustration.

All of the above said, however, it would be too facile to point to such examples as somehow representative of an entire discipline and on that basis automatically dismiss the intellectual value of said discipline. After all, in the first half of this chapter I singled out individual scientists and criticized them directly, without thereby implying in the least that science at large is therefore a thoughtless exercise, nor that scientists as a group hold to the same debatable attitudes characteristic of the likes of Weinberg, Krauss, & co. The problem of course is that all the authors mentioned so far — on both sides of the isle — are also known by, and write for, the general public. They are therefore in the unique position of doing damage to public perception of each other’s disciplines. So, let us simply admit that some scientists can write questionable things about philosophy just as some philosophers can return the favor in the case of science. But also that this does not license declarations of the death or uselessness of either discipline, and that the intellectually respectful thing to do is to seriously engage one’s colleagues across the isle, or — lacking any interest in doing so — simply keep one’s keyboard in check, once in a while.

Overcoming Philosophy’s PR problem: The next generation

What can be done in order to help philosophy out with its PR problem, other than attempting to educate some prominent physicists and perhaps gently nudge toward retirement those senior philosophers who suddenly begin to write about the evils of “Darwinism”? As it turns out, quite a bit has been done already by a number of colleagues, although the main focus so far has been on improving the field’s reputation with the public, not as much with other academics. I will briefly mention three such ventures because they are precisely the sort of thing that has helped science with its own similar issues in the past, and because they have the potential to make philosophy once again the respected profession that it was at the time in which all of Europe was enthralled by the dispute between Hume and Rousseau (Zaretsky 2009). Well, closer to that level than it is now, anyway.

The first development of note can actually be pinpointed to a specific date: on May 16, 2010 the New York Times, arguably the most prestigious newspaper on the planet, started a blog series devoted to philosophy, called The Stone. The series is curated by Simon Critchley, who is Chair of Philosophy at the New School for Social Research in New York. At the moment of this writing The Stone is still going strong, with dozens upon dozens of posts by a number of young and established philosophers, each generating vibrant discussions among New York Times readers and more widely in the blogo- and twitter- spheres. As it can be expected, the quality of the essays published in this sort of venue varies, but — snobbish sneering and misplaced nitpicking by some elderly colleagues notwithstanding — The Stone is an unqualified good for the profession, as it brings serious and relevant philosophy to the masses, and the masses are clearly responding positively.

Secondly, a number of publishers have began to offer series of books generally referred to as “pop culture and philosophy”: OpenCourt, Wiley, and the University Press of Kentucky are good examples. It used to be that if you were a layperson interested in philosophy you could do little more than read yet another “history of Western philosophy.” Now you can approach the field by enjoying titles such as The Big Bang Theory and Philosophy (referring to the television show, not the cosmological theory), The Daily Show and Philosophy (featuring the comedian Jon Stewart, seen as a modern day Socrates), and The Philosophy of Sherlock Holmes, among many, many others.

The last new development of the past several years in public understanding of philosophy that I wish to briefly mention is the phenomenon of philosophy clubs. They go under a variety of names, including Socrates Café, Café Philosophique, etc. In New York City alone, where I live, there are a number of successful groups of this type, a couple of which count over 2000 members, having been in existence for close to a decade. And they are by far not isolated cases, as New York is not an exceptional location (from that perspective anyway). Similar efforts have been thriving in many other American and European cities, and I don’t doubt the same is true in yet other parts of the world. There just seems to be a hunger for philosophy, and not just the “what is the meaning of life?” variety: there are cafes devoted to continental philosophy, to individual philosophers (Nietzsche is ever popular), even to reading and discussing specific philosophical tomes (often Kant’s). It is absolutely puzzling that Universities, and particularly their continuing education programs, haven’t figure out how to tap into these constituencies. Very likely they are not even aware of the existence and success of such groups.

As in the case of The Stone and of the “philosophy and...” book series, far too often I hear professional philosophers dismissing philosophy clubs, or looking down on those who spend time contributing to it. Let me be clear: not only is such an attitude snobbish and unjustified, it is self-defeating. Every academic field needs to remind the public of why it exists, why funding it is a good thing for society, and why students should bother taking courses in it. This is a fortiori true for an endeavor like philosophy, too often misunderstood by colleagues from other fields, and constantly in need of justifying its own existence both internally and externally to the academy. But as I said, the good news is, things are changing, because the snobs retire and the new generation sees involvement with the public as necessary, fruitful and, quite frankly, fun. But fun doing what, exactly? What is philosophy, really? To that question we turn next.

2. Philosophy Itself

“Wonder is the feeling of the philosopher, and philosophy begins in wonder.”
(Plato)

The central thesis of this book is that philosophy, in a non-trivial sense, makes progress, although that sense is significantly different from that of scientific progress and — I will argue — somewhere closer to progress in mathematics and logic. [5]

My interest in this question arises from a somewhat unusual academic path. I began my career as an evolutionary biologist, with an interest in gene-environment interactions (what philosophers typically refer to as nature-nurture questions). I pursued both empirical and theoretical research in that field for about a quarter of a century, and then decided that I needed to do something different. Armed with a freshly acquired degree in philosophy and a published thesis in philosophy of science (Pigliucci and Kaplan 2006) I eventually landed a job as a full time philosopher. And then the trouble began.

I quickly learned — though it should have come as no surprise, really — that philosophers are an unusual bunch of academics, at least compared to scientists. Philosophers are overly prone to question the very foundations and utility of their own discipline, in some cases (as we shall see) even going as far as agreeing with some scientists who have a bit too hastily declared philosophy dead or useless (often, precisely on the alleged ground that it doesn’t make progress, or at least not the sort of progress a scientist expects). Add to this that philosophy has of late developed a significant PR problem, as we have just seen, both with the public at large and with other academics (again, particularly scientists), and we have the recipe for a generalized crisis within one of the oldest fields of inquiry that has ever occupied human minds.

I think much of this trouble is based on common misunderstandings about what philosophy is and how it works, and that it can (and ought) to be corrected, particularly, of course, by its own practitioners. Before getting any further, however, we need to address the question that we postponed from the previous chapter: what is philosophy? Again, this is the sort of thing that only philosophers indulge in asking, while practitioners of other disciplines are more than happy to go about their business without too much self- referential pondering (they would probably say without “wasting too much time”). Indeed, the whole field of metaphilosophy is dedicated to how philosophy itself works and, by implication at least, to what philosophical investigations consist of.

It is not easy to catch philosophers on record — especially in peer reviewed publications — freely musing about how to best characterize their field. But we live in a world in which even philosophers are getting used to social media, podcasts and blogs, and it turns out that such outlets are friendlier to our quest. So for instance, Popova (2012) collected a variety of responses to the question “What is Philosophy?” from a number of prominent contemporary practitioners, and some of the answers are illuminating.

For Marilyn Adams, for instance, the point is “trying to bring analytic clarity both to the questions and the answers,” while for Peter Adamson “Philosophy is the study of the costs and benefits that accrue when you take up a certain position.” Richard Bradley says that it is “about critical reflection on anything you care to be interested in,” whereas Allen Buchanan claims that it “generally involves being critical and reflective about things that most people take for granted.” Don Cupitt simply says that philosophy is concerned with critical thinking (an unfortunately much abused term, of late); for Clare Carlisle it is “about making sense of all of this [the world and our place in it]”; and Barry Smith agrees, saying that philosophizing is “thinking fundamentally clearly and well about the nature of reality and our place in it.” For Simon Blackburn philosophy is “a process of reflection on the deepest concepts,” something that Tony Coady describes as “a science of presuppositions.” For Donna Dickenson it is about “refusing to accept any platitudes or accepted wisdom without examining it”; Luciano Floridi talks about conceptual engineering, and Anthony Kenny refers to “thinking as clearly as possible about the most fundamental concepts that reach through all the disciplines.” For Brian Leiter — arguably the most influential (and controversial) professional philosopher who blogs — a philosopher is someone who “creates new ways of evaluating things — what’s important, what’s worthwhile,” and Alexander Nehemas candidly tells us that he became a philosopher “because I wanted to be able to talk about many, many things, ideally with knowledge, but sometimes not quite the amount of knowledge that I would need if I were to be a specialist in them.” For my CUNY colleague David Papineau philosophy “requires an untangling of presuppositions: figuring out that our thinking is being driven by ideas we didn’t even realize that we had,” while Janet Radcliffe Richards regards “philosophy as a mode of enquiry rather than a particular set of subjects ... involving the kind of questions where you are not trying to find ... whether your ideas are true or not, in the way that science is doing, but more about how your ideas hang together.” Michael Sandel, a veritable star of public philosophy, opines that philosophizing means “reflecting critically on the way things are. That includes reflecting critically on social and political and economic arrangements. It always intimates the possibility that things could be other than they are.” Finally, Jonathan Wolff identifies philosophical problems as those that “arise ... where two common-sense notions push in different directions, and then philosophy gets started.” (The survey also reported somewhat uninformative or purely poetic concepts of philosophy, such as “Philosophy is the successful love of thinking,” or “When nobody asks me about it, I know. But whenever somebody asks me about what the concept of time is, I realize I don’t know,” for which — I have to admit — I have little patience.)

Obviously, the above survey is entirely informal and biased in a number of ways (particularly toward Western philosophers, many close to the so-called analytic tradition — more on this below), but then again, there does not seem to be much call for social science inquiries into the thought patterns of philosophers (with the exception of some “experimental philosophy,” to which we’ll get in due time). Still, when I read the above and other definitions included in Popova’s informal survey I actually felt encouraged. Despite the tendency to exaggerate differences, there are obvious threads emerging from the opinions of the various philosophers interviewed.

Indeed, the above is essentially a summary of what I — naively — thought of philosophy before approaching the field professionally: it is about reason, logic, arguments and analysis, not empirical evidence per se, though of course it better be informed by the best of what we know of how the world works, particularly from science; it is about examining common notions and discovering that they are more complex than often thought, or perhaps even arriving at the conclusion that they are incoherent; it is about the kind of broad thinking that helps us understand our reality as human beings in the vast universe described by science; and it has practical consequences for how we conduct our lives and structure our societies. In a sense, then, philosophy is a family resemblance, or cluster, concept, in the way Wittgenstein (1953, #65-69) thought many interesting human concepts are (including, as we have seen in the Introduction, the concept of progress!).

But, the properly skeptical philosopher may argue, there is a lot more to philosophy, and many more ways of philosophizing, than the little summary above hints at. In fact, even the inherent flexibility of a Wittgensteinian cluster concept may seem inadequate once we consider the differences between, say, analytic and continental philosophy, the two major “modes” in which the profession has split itself throughout the 20th century. This split, incidentally, has been questioned and downplayed of late, and it has always been far less sharp than often assumed. Nonetheless, there are important differences of style and subject matter between philosophers who express themselves within those two modes of inquiry, so I retain and discuss that distinction below. And then there is, of course, the difference between Western style, Greek-descended, philosophy and Eastern philosophies, which are in themselves incredibly diverse, with Indian, Chinese, Japanese and other traditions branching off each other, and yet overlapping among themselves and with the traditions of the West. Not to mention Islamic philosophy, African philosophy, etc. The list goes on.

This objection is to some extent appropriate, and the rest of this chapter is my way of dealing with it. I will argue in the following that my project needs to be limited to Western philosophy as classically understood, as well as to any tradition — be it internal to the West but of a “continental” flavor, or be it external, Eastern, Islamic or African — that sufficiently resembles it. This is not a value judgment, but a simple recognition of the fact that some of the activities that go under the broader aegis of “philosophy” are intellectual enterprises of a different enough nature that they need to be considered in their own right, and possibly be attributed a different name (being that the term φιλοσοφία originally used by the Greeks is already taken).

Before considering the differences between analytic and continental philosophy, as well as between the Western and Eastern traditions, however, let us entertain a novel and likely unfamiliar to philosophers, approach to the question. In what follows I enlisted the help of Simon Raper, a contributor to “Drunks&Lampposts.” Simon was as curious as I to figure out whether there is quantitative evidence of the much-talked about differences and relationships among various schools of (largely Western, in this case) philosophy. So he used two 21st century resources in a particularly ingenious fashion. First, he downloaded a file containing all the “influenced by” links for every philosopher listed on Wikipedia. [6] He then used a program called Gephi, an open software graphing platform, to visualize the influences among philosophers in the form of a network with the size of individual entries (say, for Aristotle) proportional to how many connections to other philosophers they have. Finally, Simon was able to provisionally identify different “schools” of thought by asking the program to depict in different colors groups of people whose within-cluster connections were significantly stronger than the connections to other groups. (If this sounds a lot like the Digital Humanities, it’s because it is. But let’s wait until later in the book to debate the pros and cons of the particular approach.)

The results are visually stunning and they actually confirm what most professional philosophers might have told you beforehand. (Although this may be somewhat disappointing, I choose to interpret the outcome as confirming that the opinions of historians of philosophy are actually well grounded quantitatively. There goes the scientist in me.) For instance, one diagram presents the broadest possible picture of the field, and we can immediately discern classical philosophers (Aristotle, Plato, all the way to Descartes), continental and proto-continental ones (Hegel, Nietzsche, Heidegger, Sartre), analytical and proto-analytical fellows (Hume, Mill, Russell), as well as crucial transitional figures (chiefly Kant and Wittgenstein). [7]

A close up of the continental tradition clearly shows Hegel and Nietzsche looming large, followed in importance (as measured, remember, by the number of connections to others — no intrinsic value judgment is implied here) by Kierkegaard, Husserl, Heidegger, Sartre, and Arendt and, to a lesser extent, by Foucault, Derrida and others.

A third diagram displays the area of the connectogram occupied by British empiricism, American pragmatism, and the modern analytical tradition. Here we clearly see the towering influence of Hume and Wittgenstein mentioned above, followed by figures like Locke, Mill, Russell, James and, interestingly, Chomsky.

With this bird’s eye view in mind, let us now turn to a more traditional, peer-opinion based, discussion of the different ways of doing philosophy and how they may or may not constitute a coherent body (as I mentioned above, I do not think they do, which is why for the rest of the book I will limit myself to a subset of that larger set). It should go without saying it, but I hope the reader is not expecting an in-depth treatment of either the analytical-continental divide or, much less, of the differences between Western and Eastern philosophies (and I am not even touching the Islamic and African traditions, with which I am unfortunately much less familiar. I hope someone else will take up that task). Each one of those endeavors, to be conducted properly, would require a book-length treatment in its own right. In this chapter, and really throughout the book, I will instead trade in-depth analysis for a broad perspective, with all the advantages and pitfalls that such a strategic decision usually implies. End of the necessary apologia.

Western vs Eastern(s) philosophies?

Our short tour on the varieties of philosophy begins with a brief examination of the similarities and differences between so-called Western and Eastern approaches. This is very complex and potentially exceedingly treacherous territory, which I cannot but skim before zooming into some of the nuances within the Western tradition itself. Throughout the following the gentle reader will need to keep in mind a couple of fairly large caveats: first, Eastern philosophical traditions are arguably even more heterogeneous than the Western one(s), so that any general talk of Western vs/and Eastern philosophy is strictly speaking a non-starter; second, when I will argue that some forms of Eastern philosophy should not really be considered philosophy, this is meant to be recognizing a distinction, not making a value judgment (and even when I will make something close to a value judgment, this ought to be understood as based on my values, not as a universal statement of any sort).

Perhaps a good place to start is the contrast between comparative philosophy and world philosophy (Littlejohn 2005). The aim of the former is, as the name plainly implies, to compare philosophical traditions, looking for both differences and similarities. World philosophy, instead, is after a program of unification or reconciliation of different traditions. For reasons that will be apparent soon, I am sympathetic toward the first approach but less so toward the second, and while I think there is some value in world philosophy, I will leave it entirely out of the following discussion.

Nussbaum (1997) has made very clear the sort of pitfalls to avoid in considering a comparative approach to philosophy. She warned about a number of potential problems, which we need to briefly consider, if nothing else to keep them clearly in mind for the rest of this chapter. First, there is the issue of chauvinism, which can be descriptive or normative. Descriptive chauvinism occurs when one writes about other philosophical traditions by using his own as an interpretive filter; normative chauvinism is a close companion of the descriptive variety, taking the further step of upholding one’s own tradition not just as an interpretive key to other approaches, but in order to maintain that it constitutes an inherent qualitative standard by which any other way of doing things must be judged.

Second, Nussbaum (rightly, I think) considers “skepticism” a vice in the context of comparative philosophy, where the term refers to an attitude of suspending judgment about different traditions: on the contrary, the job of the philosopher is in part to separate good thinking from bad thinking, regardless of which cultural tradition happens to have produced specific instances of the latter (a task made more palatable, perhaps, by the common observation that of course no tradition is immune from bad thinking).

Third, we need to be weary of different kinds of alleged incommensurability among traditions: this may take the form of the (ostensible) lack of feasibility of translating concepts across traditions, the (suggested) sheer impossibility of understanding a different tradition, and finally the claim that different traditions may use different (and incompatible) standards of evidence or reasoning. Now, in some instances — again, we will briefly look at examples below — I do think that there is something like true incommensurability among traditions, but it is certainly the case that this needs to be argued for, not simply assumed.

Finally, Nussbaum warns about the trap of “perennialism.” the assumption that (other) philosophical traditions do not change over time. Clearly, the Western one has — just compare the ancient Greeks with the medieval Scholastics, or even simply the analytical and continental approaches discussed below. Similarly, scholars distinguish significantly different periods within, say, Indian, Chinese, or Japanese philosophies.

The above cautionary statements notwithstanding, I will commit an infraction here and propose a type of normative chauvinism — which I think should apply not just to the comparison of Western and non-Western traditions, but also to discussions of the different types of Western traditions (both those currently operating in philosophy departments, and those constituting the standard canon of the history of Western philosophy). What I am going to do is to restrict the term “philosophy” to approaches that are based on discursive rationality and argumentation (henceforth, DRA). I hasten to say that — contra perhaps prima facie appearance — this is not an endorsement of analytical philosophy at the exclusion of the continental tradition (as we shall see in a bit), and much less is it an endorsement of Western philosophy “over” Eastern ones. This is because DRA has been a major (though not the only) mode of philosophizing since the pre-Socratics, and also because it is clearly found in non-Western traditions — it’s just the proportion of DRA vs non-DRA “ingredients,” so to speak, that differs across traditions.

Now, why would I want to make the move of limiting my treatment of philosophy to the practice of DRA? For two reasons, one historical, the other pragmatic. Historically, as is well known, the term “philosophy” comes from a Greek root meaning “love of wisdom,” and the associated practice has been — largely — one exemplifying DRA. So DRA-type philosophy broadly construed (i.e., not only in the narrower sense of the modern analytic tradition) can claim historical precedence on any other type of human activity that people may wish to characterize as philosophy. [8] Pragmatically, it seems to me that it doesn’t helps much, and actually increases the general confusion, if we use the same term for significantly different activities (and, after all, one of the points of philosophical inquiry is to get clear on the use of our language!). So, for instance, if you are invoking what can be fairly characterized as mystical insights (as some Eastern traditions do, though there are plenty of examples in the West as well), then you are doing something else (mysticism, to be precise). Similarly, if your writings do not contain arguments backed up by logical discourse but, say, appeal instead to emotional responses, then you are doing something else (literature, essayism, or other things, depending on the specifics). Again, examples can be found both within and without the Western tradition. Conversely, however, we can also find examples of prominent philosophers within the Western tradition who have used a variety of tools and approaches, and it serves us well to keep this firmly in mind: for instance, some have used stories (Plato, Rousseau, Kierkegaard), others have appealed to sources of evidence other than those favored by empiricists or by “analytic” philosophers (Plotinus, Augustine, Husserl), still more have proposed methods of argument different from the ones popular in the Anglophone tradition (Hegel, Marx, Heidegger, Foucault), and there have been those who saw philosophy as proceeding through the juxtaposition of aphorisms (Pascal, Lichtenberg, Nietzsche, Wittgenstein).

Having clarified that what I mean by “philosophy” in this book is a DRA-based activity (again, broadly construed), what happens to non-Western approaches? The answer is complex, and amounts to a highly qualified “it depends,” but here are some specifics. A good instance of largely DRA-type activity, which would therefore fall under my understanding of the word “philosophy,” is constituted by both classical Indian epistemology and logic (Gillon 2011; Phillips 2011).

Classical Indian authors deployed a set of logical tools that will be familiar to students of Western philosophy, including modus ponens, modus tollens, reductio ad absurdum, and the principle of the excluded middle, among others. Moreover, Indian logicians did not formally develop, but did implicitly use, other well recognized tools, such as the principle of non-contradiction. There are, of course, differences between Indian and Western logic, especially when it comes to the examination of the contributions of individual authors. For instance, Gillon (2010) notes that the 5th Century author Vā tsyā yana apparently thought that sound syllogisms need to be underpinned by a relation of causation, which confuses issues that are arguably best kept separate. But of course logic as a field has progressed also within Western philosophy precisely through the clarification and sometimes rejection of positions advanced by previous philosophers, so in this respect Indian classical logic is certainly no exception.

The situation for Indian classical epistemology is — as far as I understand it — a bit more complex. Similarities with the Western traditions are again easy to find. For instance, the concept of knowledge being impossible by accident is reminiscent of the idea (attributed to Plato, though there are scholarly debates about this: Chappell 2013) that knowledge is justified true belief, which in the West was not challenged until the very recent work by Gettier (1963). We also find equivalents to the Western empiricist position that the ultimate source of knowledge is perception, for instance in the Cārvāka school; interestingly, that claim was accompanied by skepticism of inferential processes, because they depend on generalizations that transcend perceptual experience (one is reminded of David Hume’s famous problem of induction, as expressed in the Treatise of Human Nature, 1739-40). Another fascinating dispute among classical Indian philosophers concerned the idea of Yogācāra, according to which perception is concept-free, a notion challenged by Bhartṛhari in the 3rd century, with reference to the baggage imposed by language, and by some “realists” who argued that some perception is actually concept-laden. Perhaps it is a stretch to draw a parallel between those ancient debates and modern discussions in (Western) philosophy of science concerned with the theory-ladeness of observations (Quine 1960; Kuhn 1963), but one can reasonably be tempted to do so.

That said, part of the Indian classical epistemological literature comprises Buddhist texts asserting the value of the nirvāṇa experience, a type of mystical insight that provides spiritual expertise. This seems to me definitely not within the province of DRA-type philosophizing, belonging instead to a tradition that proceeds independently of discursive rationality and argumentation [9] (again, tendencies of this type are however also easy to find within Western philosophy broadly construed, and they would accordingly be excluded from a treatment of philosophy as DRA-based). A similar problem is encountered when one considers Vedic texts, since the Veda are supposed to be exempt from error on the ground that they were not composed, nor were they allegedly spoken by anyone at the source. It is difficult to make sense of what this might mean outside of a mystical-religious tradition, and the infallibility of the Veda (or of anything else) is not the sort of thing that can be taken onboard in any DRA context.

Let us briefly consider for comparison another broad “Eastern” tradition, the Chinese one (Wong 2009), which is in itself remarkably distinct from the Indian one, arguably more so than any of the Western schools of thought are different from each other, though there are, naturally, influences from Indian to Chinese and then Japanese schools of philosophy, often traceable to the historical paths of influence of various religions in the respective geographical areas. Here a better case can be made for some degree of incommensurability with the Western intellectual lineage, as pointed out by Wong (2009) when he mentions that according to the Daodejing “The Way that can be spoken of is not the constant Way” and the “sages abide in nonaction and practice the teaching that is without words.” While one can perhaps make sense of talk of a “constant Way” within the logic of a given mystical tradition, it is by definition out of the question to apply a DRA- style philosophizing to an approach that is based on teaching without words. Then again, the same author points out the existence of skeptics of discursive rationality within the Western tradition (to a degree, Wittgenstein comes to mind), which raises the question of whether such skepticism does or does not belong to DRA philosophizing. This is not necessarily an easy one to answer, considering that the limits of discursive rationality itself can be explored in a discursively rational fashion, as in classical Greek skepticism (or on the basis of modern cognitive science).

Consider another example: Wong mentions Mengzi’s notion of human nature as originating from some sort of impersonal universal ordering force, a concept that is clearly at odds with modern science, and hence with the currently dominant naturalistic approach in Western philosophy. But of course plenty of equally unscientific notions (by contemporary standards) can be found throughout the history of Western philosophy itself, for instance the Stoic concept of fate, or the Platonic idea of a transcendental realm of forms. Still following Wong, it is fair to characterize Chinese metaphysics and epistemology as a type of “wisdom” literature that is weary of Western-style argumentation. Some authors have talked about the “invitational” style of Chinese philosophy (Naes and Hanay 1972), the aim of which is to make palatable a particular way of looking at and doing things, something akin to some (but definitely not all) continental Western philosophy. Wong rightly argues that the difference is of degree, not kind, citing for instance Plato’s own propensity for long and vivid descriptions in the Republic, at the expense of straightforward DRA philosophizing. Not to mention that Confucian philosophers have been criticized — and have responded to criticism — by way of arguments directed at specific aspects of their teachings.

Indeed, the similarities between Chinese and Western traditions are perhaps most obvious when it comes to ethics. Several authors have pointed out that the Confucian idea that the state is a larger version of the family would have been perfectly understandable by and debatable within the conceptual resources of ancient Greek virtue ethics. Wong (2009) goes even further, suggesting that a recent renewal of interest about Confucianism is the result of the parallels one can draw not only with Greek’s virtue ethics, but with the Western medieval and even modern approaches to ethics that rely on the concept of virtue. And Yu (2007) has proposed that the idea of dao in Confucius has strong similarities with the concept of eudaimonia. The fact that there are differences between Greek virtue ethics and Confucianism (e.g., there is no equivalent central role of the family in the first one, while the latter lacks a strong sense of individual rights) does not undermine the general point that Confucianism does come close to a type of DRA-style philosophizing, and therefore the broader point that no simple distinction can be made between Western and Eastern philosophies on the basis of the DRA criterion.

One last set of examples comes from the much discussed Kyoto school (Davis 2010), which explicitly made an attempt to merge Eastern and Western traditions, in a way that is particularly illuminating as far as our discussion of DRA vs. other styles of doing philosophy is concerned. As Davis argues, understanding the Kyoto School requires more than a straightforward framework of Eastern philosophers adopting a patina of Western philosophy, nor is it a simple matter of a “Japanization” of standard Western thought. The Kyoto philosophers were original thinkers who truly attempted a third way throughout the 20th century. This said, it is interesting to note that the School drew mostly from two influences: Mahâyâna Buddhism from the East, and clearly continental (or continental-style) authors such as Nietzsche and Heidegger from the West.

This is not the place for an in-depth discussion of the Kyoto School (nor am I qualified to lead such a discussion anyway), but it will be instructive to take a brief look at the School’s cardinal notion of “Nothingness” and how it contrasts to the Western (largely, Continental) one of “Being.” From the point of view of Kyoto exponents, Western philosophy is characterized by “the question” of Being, which — though in very different forms — can be traced from Aristotle to Heidegger. For Aristotle and much of the pre-modern Western tradition, Being was to be conceptualized as substance, which could then be instantiated in either particular or universal form. Within that framework, it makes sense to ask questions about, for instance, whether there is a highest being (Aristotle’s Prime Mover, or the God of Christian theologians), though Heidegger shifted the discussion in an even more esoteric direction.

The Kyoto counter to the notion of Being is the idea of Nothingness, which is very hard to wrap one’s mind around when coming from outside of the specific cultural ancestry that led to it. Kyoto philosophers talk about a “meontology” as opposed to ontology, meaning a philosophy of non-being. If Heidegger is too mystical for you (as, I must admit, he is for me), you will feel even more uncomfortable with the writings of the Kyoto School. It is not by chance that Kyoto philosopher Nishitani (1990) has drawn direct parallels not just with the above mentioned Nietzsche and Heidegger, but with Christian mystical thinkers and with Neoplatonists.

When one of the major authors of the Kyoto School, Nishida (quoted in Davis 2010) writes things like: “Absolute Nothingness at once transcends everything and is that by which everything is constituted,” defines self-awareness as “self reflecting itself within itself,” or claims that the Absolute “contains its own absolute self-negation within itself” it is hard to see what sort of DRA-type defense of these claims one could possibly mount, or indeed even what these claims mean outside of the particular Buddhist Zen tradition in which they are rooted. This is also a result of the fact that — has noted by others (Heisig 2001) — the Kyoto School explicitly rejects a crucial methodological tenet of modern Western philosophy (though not, obviously, of its Medieval counterpart): a clear logical separation between religion and philosophy. That rejection, in my view, situates the Kyoto scholars closer to a non-DRA form of philosophizing. Therefore, in the specific sense explained above, they may not actually be doing philosophy, but rather something else related to philosophy in a family resemblance fashion.

Then again, some members of the Kyoto tradition do engage more directly with Western philosophers, though — tellingly — almost always of the Continental type. For instance, Ueda’s “twofold being-in-the-world” (see Davis 2010) is a form of religiously based philosophy that draws on phenomenologists like Husserl and Heidegger, the latter arguably among the closest, within modern Western philosophy, to a non-DRA mode of thinking, especially in some of his later writings. When Davis, in summarizing Ueda’s thought, says that “Ueda argues that both the ego of the Cartesian cogito, as well as the non-ego of Buddhism, must ultimately be comprehended on the basis of an understanding of the self as a repeated movement through a radical self-negation to a genuine self- affirmation,” it is again a bit difficult to see — from a DRA-perspective — in what sense one can “argue” or unpack this. So of what style of philosophizing is the Kyoto School an example, in the end? Davis (2010) himself concludes his review with a mixed message in this respect. On the one hand, he acknowledges that it is reasonable to see the Kyoto writings, while being the result of a dialogue with the West, clearly as a reflection of a largely Eastern (and, specifically, Zen Buddhist) tradition. On the other hand, some Kyoto authors are to be interpreted as appropriating a Hegelian style of dialectical logic, and not as reflecting Buddhist thought in any straightforward manner. Interestingly, the Kyoto philosophers themselves are pretty clear that the term philosophy — just as I have argued above — is historically a result of Western thought, and is therefore markedly distinct from the Eastern roots of the School. However, the claim is also that the Kyoto School is sympathetic to the idea of a philosophy that transcends any East-West divide, in analogy to the fact that there is no such thing as Western vs Eastern science or technology. I am not so sure that that particular analogy actually stands up to critical scrutiny, for the reasons explained above. Indeed, (modern) science very much proceeds by the same general methods and standards of evidence worldwide, and its products are directly comparable to each other, regardless of where the research has been conducted (Newtonian mechanics isn’t culturally relative). By contrast, I would not know how to explain in what sense a philosophy of Nothingness is comparable to a lot of what dominant styles of Western philosophy have produced. Davis wraps up his commentary on the Kyoto School with a bold call to action: “If philosophy today is to mature beyond its Eurocentric pubescence, then it is necessary to deepen its quest for universality by way of radically opening it up to a diversity of cultural perspectives.” But I am not at all convinced that DRA-type philosophy (Western or not) can seriously be thought of as “pubescent” after more than two and a half millennia of practice, nor am I confident at all that indiscriminate embracing of all other traditions that may call themselves philosophical is actually a project worth pursuing.

So much for East and West, then. Let us now zoom into modern Western philosophical practice and take on another allegedly deep divide between ways of doing philosophy: the infamous distinction between analytic and continental modes of philosophizing.

Analytic vs. Continental?

As is well known, perhaps one of the most controversial, often even acrimonious (Levy 2003), splits in modern Western philosophy is the one between the so-called “analytic” and “continental” approaches. Even though lately the fashion in philosophical circles is actually to deny outright that there is any meaningful distinction to be made in this context, I think to ignore this aspect of modern philosophizing would do a disservice to the field and to its practitioners. And as it will soon be clear, plenty of people keep making interesting comments on the analytic-continental distinction even though it allegedly does not exist (e.g., Mulligan et al. 2006).

To simplify quite a bit, the split has become apparent during the 20th century, though it can be traced back to the immediately post-Kantian period (with Kant himself often depicted as straddling the two traditions). Analytic philosophy refers to a style of doing philosophy characteristic of the modern British empiricists, like Moore and Russell, with an emphasis on argument, logical analysis, and language, and it is what one finds practiced in many (though by no means all) philosophy departments in the United States and the UK. Michael Dummett (1978, 458) famously said that the “characteristic tenet [of analytic philosophy] is that the philosophy of language is the foundation for all the rest of philosophy ... [that] the goal of philosophy is the analysis of the structure of thought [and that] the only proper method for analysing thought consists in the analysis of language.” However, Cooper (1994) rightly points out that this is only partially helpful when it comes to distinguishing analytic philosophy, especially in the light of recent developments, such as the rise of “analytic metaphysics” (Chalmers et al. 2009). Continental philosophy — the name deriving from the fact that historically its leading figures have been German or French thinkers — is seen as a more discursive, even polemical, way of doing philosophy, often characterized by a not entirely transparent way of presenting one’s ideas, and more concerned with social issues than its analytic counterpart (though, again, there are plenty of exceptions).

There are two questions that concern me here: how can we understand the nature of the split and what it says about philosophy in general? And to what extent is some of what is going under the heading of continental philosophy sufficiently different from the core discipline and its tools that we might want to think of it as a different type of activity altogether? Richard Rorty (1991, 23) famously answered the second question somewhat categorically, foreseeing a day when “'it may seem merely a quaint historical accident that both bear the same name of ‘philosophy.’” I’m not so sure.

Perhaps the first thing that becomes obvious when comparing analytic and continental works is their difference in style. As Cooper (1994) puts it, “We know where Quine or Derrida belongs, before grasping what he is saying, from the way he says it.” Levy (2003) characterizes continental philosophy as more “literary” as opposed to the (allegedly) clearer but more rigid analytic approach. As we shall see in a moment, this difference in style also points toward a deeper division between the two modes of doing contemporary Western philosophy: one more “scientific” (and science-friendly), the other more humanistic (and often critical of science). Another consequence manifests itself in the type of work produced in the two traditions, as well as in the makeup of their intended audiences: with the usual caveat that there are a number of exceptions, analytic philosophers increasingly prefer scholarly papers to books (as do scientists, nowadays), and aim them primarily at a very restricted set of specialists; continentalists, by and large, prefer books which, at least to some extent, are meant to engage the general educated public, not in the sense of being introductions to philosophy, but in that of fashioning the philosopher in the role of a cultural critic with broad appeal.

I find Cooper’s (1994) analysis of the two modes of philosophical discourse particularly convincing, though I will integrate it with the one proposed by Levy (2003), who also builds on Cooper, and of course with my own considerations. According to Cooper, the best way to understand the difference between analytic and continental styles is in terms of three themes present in the latter and either absent or of reduced importance in the former, and to realize that the different styles are in turn underlined by a fundamental difference in mood between practitioners of the two traditions. [10]

The three themes identified by Cooper are: cultural critique, concern with the background conditions of inquiry, and what for lack of a better term he calls “the fall of the self.” Cultural critique is perhaps the chief activity continental philosophers are associated with in the mind of the general European public, particularly in France (think Foucault and Derrida). This it is the sort of thing that relatively few analytical philosophers dabble in, and when they do — as astutely observed by Cooper in the case of Bertrand Russell and his social and anti-war activism — it is in an “off duty” mode, as if the thing had little connection with their “real” work as philosophers.

As far as the second theme is concerned, both analytic and continental philosophers are preoccupied with the conditions for inquiry and knowledge, but from radically different perspectives. As I shall elaborate upon below, philosophy of science (which is for the most part firmly planted in the analytic tradition) approaches the issue from the point of view of logic and epistemology, with talk of logical fallacies, validation of inferences, testability of theories, and so on. On the other side we have “science studies,” a heterogeneous category that includes everything from philosophy of technology to feminist epistemology, with more than an occasional dip into postmodernism. Here the emphasis is on science as a source of power in society, on the social and political dimensions of science in particular, and on the construction of knowledge in general.

The third of Cooper’s themes — the “fall of the self” — is also shared by the two traditions, in a sense, but again the two approaches are almost antithetical. Analytical philosophers generally tend to have a deflating if not downright eliminativist attitude toward “the self,” dismissing outright any form of Cartesian dualism as little more than a medieval superstition, and in some cases arriving at what some of them think is a science-based conclusion that there is no such thing as “the self” or even consciousness at all, yielding something that looks like a strange marriage of cognitive science and Buddhist metaphysics. Continental philosophers do not mean anything like that at all when they talk about the self, the death of the author, or the death of the text — though what exactly they do mean has in many instances been more difficult to ascertain.

For Cooper these three thematic differences are in turn rooted into a fundamental difference of philosophical mood: to put it a bit simplistically, analytic philosophers are sons (and daughters) of the Enlightenment, and they are by and large very sympathetic toward the scientific enterprise, even to the point of using it (wrongly, I will submit later in the book) as a model for philosophy itself. Just consider Russell’s (1918) classic essay, “On the scientific method in philosophy.” Continentalists, on the contrary, tend to be markedly anti-scientistic (in some cases, to be honest, downright anti-science), and are instinctively suspicious of claims of objective knowledge made by cadres of experts. Just think of Foucault’s (1961) classic work on madness. From the continental point of view, philosophers of science like Popper (1963) are hopelessly naive when they look (and think they find) logical rules that can determine the validity of scientific theories, and authors in the continental mode would argue that too much emphasis on a scientific worldview ends up discounting the human dimension altogether — ironically, philosophy’s original chief concern (at least according to Plato). Indeed, if one reads, say analytical philosopher Alex Rosenberg’s (2011) The Atheist Guide to Reality one is cheerfully encouraged to embrace nihilism because that’s where fundamental physics leads to (in his opinion). Imagine how Camus would have reacted to that one.

Cooper’s analysis also provides the point of departure for Levy’s, which leads the latter to add an interesting, if in my opinion debatable, twist. Somewhat ironically, Levy uses Thomas Kuhn’s (1963) ideas on the nature of science as a way to separate the analytical and continental modes of philosophizing. I say ironically because Kuhn is claimed to some extent by both camps: among philosophers of science (analytic) he is credited to have been the first to take seriously the historical-cultural aspects of science, not just the logical-formal ones. From the perspective of science studies (continental) he is associated with having dismantled the idea of objective progress in science, an “accomplishment” he himself vehemently denied.

Levy’s idea is that analytic philosophy has modeled itself as a type of activity akin to Kuhn’s “normal,” or “puzzle-solving,” science, i.e. science working within an established paradigm, deploying the latter to address and resolve specific issues. The paradigm Levy has in mind for analytic philosophy is chiefly the result of the works of Frege and Russell, i.e. an approach that frames philosophy in terms of logic and language. As in normal science, analytical philosophers therefore specialize on highly circumscribed “puzzles,” and Levy is ready to grant (though he leaves the notion unexplored) that such philosophy makes progress — in a way similar to that, say, of evolutionary biologists working within the Darwinian paradigm, or physicists operating under the Standard Model (sans the empirical data as far as philosophy is concerned, naturally). However, this depth of scholarship inevitably trades off against an inability to address broadly relevant issues (just like in normal science, according to Kuhn).

That’s where — in Levy’s analogy — the contrast with continental philosophy becomes evident. The latter functions rather in a perpetual state of Kuhnian revolution, moving from one paradigm to the other (presumably, without ever experiencing significant periods of puzzle-solving in the middle). In a sense, argues Levy, continental philosophy models itself after modernist art, where the goal is not to make progress, at least not in the sense of gradually building on the shoulders’ of previous giants, but to completely replace old views, to invent fresh new ways of looking at the world.

The trouble with this model, as Levy himself acknowledges, is that it makes the two philosophical modes pretty much irreconcilable: “If this [view] is correct, we have little reason to be optimistic that AP [analytic philosophy] and CP [continental philosophy] could overcome their differences and produce a new way of doing philosophy that would combine the strengths of both.” But perhaps such pessimism is a bit hasty. Let us consider one possible way in which the two traditions may be merged into a third way that emphasizes the strengths of both and minimizes their respective weaknesses.

A case study: philosophy of science vs science studies

Contra Levy, I do think there is quite a bit that can be done to reconcile analytical and continental approaches, combining them into a (newly) expanded view of philosophy that has both depth and breadth, and is concerned both with specific technical “puzzles” and with broad socio-political issues. I will use the contrast drawn above between philosophy of science (largely analytical) and “science studies” (more continental) as an example of where the differences lie and how to overcome them. Not everything will be rosy in the picture that I propose, since what some analytical philosophers have been up to may indeed turn out to be somewhat irrelevant, while what some continentalists have been arguing will reveal itself as pretty debatable to say the least. Still, it is far more preferable to seek the best of both worlds than to dwell on their respective worst. Let us begin with a thumbnail sketch of the two approaches to the study of the nature of science. Philosophy of science, as it has been understood throughout the 20th century, is concerned with the logic of scientific theories and practices, which range from broad questions about science at large (say, whether falsifiability of scientific theories is a valid criterion of progress: Popper 1963 vs Laudan 1983, 111) to fairly narrowly defined problems within a given special science (e.g., the concept of biological species: Brigandt 2003; Ereshefsky 1998; Pigliucci 2003). In other words, philosophy of science is a type of analytical practice, where one is concerned with the logic of arguments and the logical structure of concepts, in this case those deployed by scientists in the course of their work.

Science studies — as I am using the term here — is a bit more fuzzy, as it includes a number of approaches to the study of science that are not necessarily compatible with each other in a straightforward manner. This includes philosophers who use what may be termed an ethnographic approach to science (e.g., Latour and Woolgar 1986), those who are interested in cross-cultural comparisons among similar types of science laboratories (Traweek 1988), and those who take a feminist approach to scientific epistemology (Keller 1983; Longino 1990), among others. What these authors have in common is a focus on the social and political dimensions of science, which is seen primarily as a human activity characterized by ideologies and issues of power.

The clash between the two perspectives has led to the already mentioned “science wars” of the 1990s, of which the iconic moment was represented by the highly controversial “Sokal affair” (Sokal and Bricmont 2003). As is well known, New York University physicist Alan Sokal, fed up with what he perceived (at the least in part, it must be said, rightly) as postmodernist nonsense about science, concocted a fake paper entitled “Transgressing the Boundaries: Towards a Transformative Hermeneutics of Quantum Gravity,” submitted it to the editors of the prestigious postmodernist journal Social Text, and managed to get it published before exposing it as a hoax. While certainly shaming for the editors involved, and a highly visible black mark for a certain way of criticizing science, the import of the affair should probably not have been as large as it turned out to be. Sokal himself recognized that one can hardly impugn an entire tradition of scholarship on the basis of one editorial mistake, particularly given that Social Text is not even a peer reviewed publication. Nonetheless, one can understand the frustration of scientists (and of analytical philosophers of science) in the face of, for instance, extreme feminist epistemology, where one author boasts (with little to back up her rather extraordinary claim) that “I doubt in our wildest dreams we ever imagined we would have to reinvent both science and theorizing itself” (Harding 1989); or of Bruno Latour’s (1988) scientifically naive psychoanalytical re- interpretation of Einstein’s theory of general relativity.

What got lost in the kerfuffle is that of course science is both an epistemic activity that at least strives for (and has been historically remarkably successful at) a rational use of evidence and a social activity with inevitable ideological, political and even personal psychological components playing a non inconspicuous part in it. In some sense, this is nothing new. John Stuart Mill, one of the early “philosophers of science” (in the broadest sense of the term, which of course was not in use at the time) was well aware of the fallibility of science as a human enterprise (Longino 2006), which brought him to the conclusion (similar to Longino 1990, the latter arrived at from a feminist perspective) that the best science is the result of collective cross-criticism. But Mill was also very much a philosopher of science in what would later become the analytical sense of the term, for instance engaging in a famous debate with Whewell (Whewell 1847; Mill 1874) on the nature of induction.

It is, further, not the case that 20th century philosophers of science completely ignored the social (and even historical) dimension of science. That is what made Kuhn’s (1963) famous work so notable (and controversial). And of course let us not forget the radical critique of science produced by enfant terrible Paul Feyerabend (1975). While neither Kuhn nor Feyerabend can reasonably be considered part of the postmodern-continental tradition, they have both been invoked as forerunners of the latter when it comes to science studies — Feyerabend would have likely be pleased, while Kuhn certainly would have declined the honor. Both of them made points that should provide part of a blueprint for an expanded philosophy of science, albeit not necessarily following the exact lines drawn by these two authors. For instance, Feyerabend was simply (and purposefully) being irritating when — in what sounds like a caricature of postmodernism — he said that the only absolute truth is that there are no absolute truths, or when he wrote “three cheers for the fundamentalists in California who succeeded in having a dogmatic formulation of the theory of evolution removed from textbooks and an account of Genesis included” (Feyerabend 1974). Then again, he did realize that said fundamentalists from California would soon become a center of power in their own right and cause problems in turn: “I have no doubt that they would be just as dogmatic and close-minded if given the chance.” A more equitable assessment of the situation might be that religious fundamentalists are much more likely than mainstream scientists to be dogmatic and close-minded, but that this doesn’t imply that scientists cannot be or have not been as well.

Kuhn — who interestingly started out as a physicist, moving then to history and philosophy of science — contrasted his descriptive approach to understanding how science works with Popper’s more traditionally prescriptive one. While Popper (and others) pretended to tell scientists what they were doing right (or wrong) based on a priori principles of logic, Kuhn wanted to figure out how real science actually works, and one sure way of doing this is through historical analyses (another one, taken up by many scholars in the continental tradition, is to do sociology of science). The reason he became a precursor of certain types of science studies, and at the same time got into trouble with many in philosophy of science, is that his model of normal science equilibria punctuated by paradigm changes does not have an immediate way to accommodate the idea that science makes progress. This was not, apparently, Kuhn’s intention, hence his 1969 postscript to clarify his views and distance himself from a more radically postmodern reading of The Structure of Scientific Revolutions. Again, though, it seems to me that in Kuhn as in Feyerabend there is a tension that is not really necessary: one can reasonably argue that science is a power structure prone to corrupt if left unchecked, and yet not go all relativist and say that it is thereby no different than a fundamentalist church. Equally, one can stress the importance of both historical and sociological analyses of science without for that reason having to throw out the value of logic and epistemology.

Can the insights and approaches of philosophy of science and science studies be reconciled to forge a better and more comprehensive philosophy of science? Yes, and this project has already been under way for close to three decades, a synthesis that constitutes my first clear example of (conceptual) progress in philosophy. While there are a number of scholars that could be discussed in this context, not all of them necessarily using the same approach, I am particularly attracted to what Longino (2006) calls “reconciliationists,” a group that includes Hesse (1974, 1980), Giere (1988), and Kitcher (1993). Giere, for instance, applies decision theory to the modeling of scientific judgment, which allows him to include sociological parameters as part of the mix. His approach later led him to formulate a broader theory of the nature of science from a “perspectivist” standpoint (Giere 2010). The analogy introduced and developed by Giere is with color perception (hence the name of the approach): there is no such thing as an absolutely objective, observer-independent, perception of color; and yet it is also not the case that color perception is irreducibly subjective. This is because the perception of color is the result of two types of phenomena: on the one hand, color is the outcome of observer-independent facts, such as diffraction and wavelength of incident light on physical objects with certain surface characteristics; on the other hand, it is made possible by the brain’s particular way of interpreting and transducing external stimuli and internal electrical and chemical signals. Similarly, science is a process by which the objective, mind-independent external world is understood via the psychological and sociological factors affecting human cognition. The result is a (inherently subjective, yet often converging) perspective on the world. A nice compromise between the “view from nowhere” assumed by classical philosophers of science and the irreducible relativism of postmodern science studies.

Hesse’s (1974, 1980) approach is intriguing in its own right, and builds on Quine’s concept of human knowledge as a “web of belief” (as opposed to, say, an edifice of knowledge/belief, an image which raises endless and futile questions concerning the “foundations” of such edifice: Fumerton 2010). Hesse reaches even further back, to the work of Duhem as presented in the latter’s The Aim and Structure of Physical Theory, even though modern scholars recognize important distinctions between the views of Duhem and those of Quine in this respect (Ariew 1984). The basic idea is to build a Duhem- Quine type web of belief, some of the elements of which are not just scientific facts and theories, but also social factors and other criteria that go into the general practice of science: “there is [thus] no theoretical fact or lawlike relation whose truth or falsity can be determined in isolation from the rest of the network. Moreover, many conflicting networks may more or less fit the same facts, and which one is adopted must depend on criteria other than the facts: criteria involving simplicity, coherence with other parts of science, and so on” (Hesse 1974, 26). While this is far more permissive than perhaps a strict logical positivist might like, it is certainly no nudge in the direction of Feyerabend-like methodological anarchism, and much less is it of any comfort to epistemic relativism.

What I have presented here, of course, is but a sketch of a large and continuously evolving field within the broader scope of philosophy. Nevertheless, I think I have made a reasonable argument that analytical and continental approaches to the study of science can both be pruned of their excesses or dead weight, as well as that the best of the two traditions can (indeed, should) be combined into a more vibrant and relevant conception of philosophy of science. As a bonus, we have also just encountered our first example of how philosophy makes progress.

By now the reader should have a better overall picture of what philosophy is, and of why it is a distinctive, and yet somewhat inclusive, type of intellectual inquiry. The fundamental contrast, as I see it, is neither between analytical and continental approaches, nor between East and West. It is not even one of specialization vs generalism, or of particular subject matters that are or are not amenable to philosophizing. The distinctive characteristic of philosophy in the sense I use the term throughout this book is its DRA nature: to do philosophy means to engage in discursive rationality and argumentation. As we will see next, for much of the 20th century, at the least in the Western world, this has meant using science as a model to emulate and an arbiter to invoke, in what is sometimes referred to as the “naturalistic” turn.

3. The Naturalistic Turn

“To be is to be the value of a variable.”
(Willard Van Orman Quine)

We have seen so far that philosophy broadly construed has a significant public relation problem, and I’ve argued that one of the root causes of this problem is its sometimes antagonistic relationship with science, mostly, but not only, fueled by some high prominent scientists who locked horns with equally prominent anti-scientistic philosophers. In this chapter we will examine the other side of the same coin: the embracing by a number of philosophers of a more positive relationship with science, to the point of either grounding philosophical work exclusively in a science-based naturalistic view of the world, or even of attempting to erase any significant differences between philosophy and science. This complex discourse is sometimes referred to as the “naturalistic turn” in modern analytic philosophy, it arguably began with the criticism of positivism led by Willard Van Orman Quine and others in the middle part of the 20th century, and it is still shaping a significant portion of the debate in metaphilosophy, the subfield of inquiry that reflects critically on the nature of philosophy itself (Joll 2010).

Two very large caveats first. To begin with, which philosophy am I talking about now? We have seen earlier that the term applies to a highly heterogeneous set of traditions, spanning different geographical areas, cultures, and time periods. To be clear — and for the reasons I highlighted in the last chapter — from now on and for the rest of the book I will employ the term “philosophy” to indicate the broadest possible conception of the sort of activity began and named by the pre-Socratics in ancient Greece, what I termed the DRA (discursive rationality and argumentation) approach. This will comprise, of course, all of the current analytic tradition, but also parts of continental philosophy, and certain aspects or traditions of “Eastern” philosophies. It will also include the work of modern and contemporary philosophers that do not fit easily within the fairly strict confines of proper analytic philosophy: both versions of Wittgenstein, for instance, at least some strains of feminist philosophy, and much more. If this sounds insufficiently precise that is — I think — a reflection of the complexity and richness of philosophical thought, not necessarily a shortcoming of my own concept of it.

Secondly, it must be admitted that venturing into a discussion of “naturalism” is perilous, for the simple reason that there is an almost endless variety of positions within that very broad umbrella, and plenty of people who feel very strongly about them. In the following, however, I will focus specifically on approaches to naturalism (and the philosophers who pursue them) that are most useful or otherwise enlightening for the general project of this book, which largely involves the relationships between science and philosophy and how they both make progress, albeit according to different conceptions of progress.

Basic metaphilosophy

Before tackling naturalism, we need to indulge in a bit more of what is referred to as “metaphilosophy,” i.e., philosophizing about the nature of philosophy itself. We have already examined what a number of contemporary philosophers think philosophy is, and I argued that there is significantly more agreement than a superficial look would lead one to believe, certainly more than the oft-made comment that every philosopher has a (radically) different idea of what the field is about. Arguably the most famous characterizations of philosophy were those given by two of the major figures in the field during the 20th century, Alfred Whitehead and Bertrand Russell. Whitehead quipped that all (Western) philosophy is a footnote to Plato, meaning that Plato identified all the major areas of philosophical investigation; a bit more believably, Russell commented that philosophy is the sort of inquiry that can be pursued by using the methods first deployed by Plato. The fact is, discussions concerning what the proper domain and methods of philosophy are (i.e., discussions in metaphilosophy, regardless of whether explicitly conducted in a self-conscious metaphilosophical setting) have been going on since at least Socrates. Just recall his famous analogy between his trade and the role of a midwife, which conjures an image of the philosopher as a facilitator of sound thinking; or Plato’s relentless attacks against the Sophists, who thought of themselves as legitimate philosophers, but were accused of doing something much closer to what we would consider lawyering.

I think it is obvious that Whitehead was exaggerating about all philosophy being a footnote to Plato, regardless of how generous we are inclined to be toward the Greek thinker. Not only there are huge swaths of modern philosophy (most of the contemporary “philosophies of,” to which we will return in the last chapter) which were obviously inaccessible to Plato, but he (and especially Socrates) made it pretty clear that they had relatively little interest in natural philosophy, with their focus being largely on ethics, metaphysics, epistemology (to a point), and aesthetics. It was Aristotle that further broadened the field with the development of formal logic, as well as a renewed emphasis on the sort of natural philosophy that had already took off with the pre-Socratics (particularly the atomists) and that eventually became science.

A rapid survey of post-Greek philosophy shows that different philosophers have held somewhat different views of the value of their discipline (Joll 2010). Hume, for instance, wrote that “One considerable advantage that arises from Philosophy, consists in the sovereign antidote which it affords to superstition and false religion” (Of Suicide, in Hume 1748), thus echoing the ancient Epicurean quest for freeing humanity from the fears generated by religious superstition. This somewhat practical take on the value of philosophy was also evident — in very different fashions — in Hegel, who thought that philosophy is a way to help people feel at home in the world, and in Marx, who famously quipped that the point is not to interpret the world, but to change it.

With the onset of the 20th century we have the maturing of modern academic philosophy, and the development of more narrow conceptions of the nature of the discipline. The early Wittgenstein of the Tractatus thought that philosophy is essentially a logical analysis of formal language (Wittgenstein 1921), which was naturally well received by the logical positivists that were dominant just before the naturalistic turn with which we shall shortly concern ourselves. Members of the Vienna Circle went so far as promulgating a manifesto in which they explicitly reduced philosophy to logical analysis: “The task of philosophical work lies in ... clarification of problems and assertions, not in the propounding of special ‘philosophical’ pronouncements. The method of this clarification is that of logical analysis” (Neurath et al. 1973 / 1996). From these bases, it was but a small step to the forceful attack on traditional metaphysics mounted by the positivists. Metaphysics was cast aside as a pseudo-discipline, and prominent continental philosophers — especially Heidegger — were dismissed as obfuscatory cranks.

I think it is fair to say that a major change in the attitude of practicing philosophers toward philosophy coincided with the diverging rejections of positivism that are perhaps best embodied by (the later) Wittgenstein and by Quine. We will examine Quine in some more detail in the next section, since he was pivotal to the naturalistic turn. The Wittgenstein of the Investigations shifted from considering an ideal logical language to exploring the structure — and consequences for philosophy — of natural language. As a result of this shift, Wittgenstein began to think that philosophical problems need to be dissolved rather than solved, since they are rooted in linguistic misinterpretations (cfr. his famous quip about letting the fly out of the fly bottle, Investigations 309), which led to his legendary confrontation with Karl Popper, who very much believed in the existence and even solvability of philosophical questions, especially in ethics (Edmonds and Eidinow 2001).

Most crucially as far as we are concerned here, the Wittgenstein of the Investigations was critical of some philosophers’ envy of science. He thought that seeking truths only and exclusively in science amounts to a greatly diminished understanding of the world. In this Wittgenstein clearly departed not just from the attitude of the Vienna Circle and the positivists in general, but also from his mentor, the quintessentially analytic philosopher Bertrand Russell. It is because of this shift between the early and late Wittgenstein that — somewhat ironically — both analytic and continental traditions can rightfully claim him as a major exponent of their approach. [11]

This very brief metaphilosophical survey cannot do without a quick look at the American pragmatists, who developed a significantly different outlook on what philosophy is and how it works. Recall, to begin with, their famous maxim, as articulated by Peirce (1931-58, 5, 402): “Consider what effects, which might conceivably have practical bearings, we conceive the object of our conception to have. Then, our conception of these effects is the whole of our conception of the object.” Peirce and James famously interpreted the maxim differently, the first one referring it to meaning, the latter (more controversially) to truth. Regardless, for my purposes here the pragmatists can be understood as being friendly to naturalism and science, and indeed as imposing strict limits on what counts as sound philosophy, albeit in a very different way from the positivists.

I find it even more interesting, therefore, that the most prominent — and controversial — of the “neo-pragmatists,” Richard Rorty, attempted to move pragmatism into territory that is so antithetic to science that Rorty is nowadays often counted among “continental” and even postmodern philosophers. His insistence on a rather extreme form of coherentism, wherein justification of beliefs is relativized to an individual’s understanding of the world, (Rorty 1980), eventually brought him close to the anti-science faction in the so-called “science wars” of the 1990s and beyond (see the chapter on Philosophy Itself). He even suggested “putting politics first and tailoring a philosophy to suit” (Rorty 1991, 178). But that is not the direction I am taking here. Instead, we need to sketch the contribution of arguably the major pro-naturalistic philosopher of the 20th century, Quine, to lay the basis for a broader discussion in the latter part of this chapter of what naturalism is and what it may mean to philosophy.

Willard Van Orman Quine

“Belief in some fundamental cleavage between truths that are analytic, or grounded in meanings independently of matters of fact, and truths that are synthetic, or grounded in fact” and “reductionism: the belief that each meaningful statement is equivalent to some logical construction upon terms which refer to immediate experience.” These are the famous two “dogmas” that W.V.O. Quine imputed to positivism (Quine 1980: 20), and that he proceeded to dismantle in one of the best examples of progress in contemporary philosophy. As we shall see, the rejection of a sharp distinction between analytic and synthetic truths, as well as the abandonment of the strict logicism of the positivists, do not necessarily amount to the complete abandonment of “first philosophy” (i.e., philosophizing to be done independently of any empirically-driven scientific investigation). Nor does it follow that philosophy blurs into science to the point of subsiding into it, a position not exactly championed by Quine, but to which he came perilously close. Regardless, one cannot talk about progress in philosophy, and especially about the naturalistic turn, without taking Quine seriously.

I do not have the space to get into an in-depth analysis of the history of positivism and the reactions it engendered by the likes of Quine, Putnam and others (see, for instance, chapters 3-6 of Brown 2012). Nonetheless, the transition from positivism to Quineian post-positivism is a very good example of what I am arguing for in this book: philosophy makes progress by exploring, refining and sometimes rejecting positions in the vast conceptual space pertinent to whatever it is that certain philosophers are interested in, in this case the nature of epistemology and the foundations of knowledge. The positivists did indeed make far too much of the analytic/synthetic distinction, which in turn leads to the notion that certain types of knowledge are possible a priori, and that therefore there is ample room for an ambitious kind of “first philosophy.” They also went too far in their peculiar form of “reductionism,” an approach to meaning that excluded not just a lot of philosophy, but even a good chunk of science from consideration, on the ground that it is (allegedly) literally meaningless. But the positivists themselves were attempting to make progress by reacting, among other things, to the excesses of a metaphysics that sounded either Scholastic or obscure (e.g., their sharp criticisms of Heidegger). It seems to me that as a result of positivism we do indeed have a number of tools to question speculative metaphysics, and even excessively speculative science (e.g., string theory: Smolin 2007); and as a result of Quine’s criticism of positivism we have the outline of a naturalistic epistemology, metaphysics, and indeed philosophy. What we do not have, however, is the collapse of epistemology, metaphysics, and philosophy into science — pace the bold pronouncements of the sort of philosophically less than literate scientists we have encountered in the chapter on Philosophy’s PR Problem.

Quine left no doubts about what he was up to in a late reconstruction of the goals of his own work: “In Theories and Things I wrote that naturalism is ‘the recognition that it is within science itself, and not in some prior philosophy, that reality is to be identified and described’; again that it is ‘abandonment of the goal of a first philosophy prior to natural science’” (Quine 1995, 251). I will get back to what exactly it may mean to abandon the idea of a first philosophy prior to science, but it is crucial to point out that Quine immediately proceeded to “cheat” somewhat about the actual scope of his project, for instance by allowing mathematics to be treated as a science (p. 252). This is somewhat odd, or at the least controversial, considering that if there is anything that defines science it is its concern with empirical evidence about the nature of the world, and mathematics most certainly does not share this basic concern (the Pythagorean theorem is about abstract triangles, not about the clumsy variety we may actually trace on the ground or on a piece of paper). Realizing this, Quine shifted the focus to applied mathematics (p. 257), which, however, does not improve things very much, since applied mathematics is only a relatively small portion of what mathematicians actually do, and at any rate it still is not derived from (although it does apply to) the empirical realm. Mathematics thus presents a problem for Quine’s overarching denial of the existence of a priori truths. His response is ultimately to argue that mathematics is justified by the role it plays in science, and therefore by experience. But that justification seems to get things backwards, and it certainly would surprise the hell out of mathematicians and most philosophers of mathematics (e.g., Brown 2008).

In his analysis of Quine’s contribution to contemporary philosophy Hylton (2010) points out that the full force of Quine’s critique of analyticity is not understood if one focuses on standard examples of the latter, like the ubiquitous “All bachelors are unmarried.” Rather, one has to consider sentences like “Force equals mass times acceleration.” Indeed, referring to examples such as the one about bachelors, Quine himself (1991, 271) says “I recognize the notion of analyticity in its obvious and useful but epistemologically insignificant applications.” But rejecting standard examples of analytical truths such as definitions on the grounds that they are “epistemologically insignificant” begs the question of what, precisely, makes a given statement epistemologically “significant.”

And this brings us back to math: for Quine math is certainly not epistemologically insignificant, which is why his example of F = ma is interesting, particularly in light of his ongoing disagreement with logical positivists (and later the logical empiricists), especially Carnap (1937), who had a lot to say about both the analytic/synthetic distinction and the status of physical laws such as Newton’s. Now, F = ma can be interpreted in a variety of ways, including as a definition (of force, or, rearranging the equation, of either mass or acceleration), but it does not snugly fit the classic conception of analytic truth. That’s because one can argue that the equation is only true within a particular empirically-based theory of the natural world, from which it derives the meaning of its constituent terms (“F,” “m” and “a”). Its truth is not rooted in mathematical reasoning per se. Indeed, it could be argued that F = ma should not even be treated as a definition of force, but rather as an operational way to measure force. There is no explicit conceptual content in the equation, which in itself is compatible with different ideas of what force, mass and acceleration are, as long as they remain related in the way in which the equation connects them. It seems like Quine was focusing on examples like F = ma because they are the sort of statement that may have looked analytical (since it is expressed in mathematical language), but is actually closer to philosophers’ understanding of synthetic truths. This narrow focus, however, may exclude too much, somewhat undermining Quine’s bold claim that there is no such thing as a priori truths. But if the latter re-enter the game — however qualified and circumscribed — then some kind of first philosophy cannot be far behind.

A related issue here is that Quine does not admit the existence of necessary truths, a negation that would be yet another nail in the coffin of pretty much the entire enterprise of (first) philosophy, at least as classically conceived. Quine, of course, arrived at this view because he was what some have termed a “radical” empiricist, and if there is one thing that empiricists abhor is the very idea of necessary truth. Indeed, for Quine even logic was — at least potentially — on the chopping block of his version of a naturalized philosophy. But another major philosopher of the 20th century, Kripke (certainly not a naturalist [12]), argued shortly thereafter that there is a new way of conceiving of necessary truths: in modal logic, these become truths that hold in all possible worlds (Kripke, 1980). The caveat with Kripke’s reintroduction of necessary truths is that they turn out to be so a posteriori, as in the famous example of whether water is necessarily H2O, something that can be answered only by science, and therefore on empirical grounds. A posteriori necessary truths are controversial in philosophy, but for the purpose of our current discussion they count as a type of necessary truth, and of course they do not exclude the possibility of more standard, a priori necessary truths anyway. Indeed, Kripke insisted that he was making an ontological point about the existence of a priori truths; how we find out about them (scientific investigation = a posteriori, philosophical reasoning = a priori) is an epistemological issue. Considering again F = ma, Kripke’s point would be that the equation, if expressed as an identity statement, would be both necessarily true and known a posteriori.

The broader context of this discussion is provided by Quine’s views of metaphysics and epistemology, which are in turn related to his idea of knowledge as a “web of beliefs,” a metaphor that I very much like, with some caveats. Let us begin by tempering the web-of- beliefs metaphor the way the master himself did: “It is an uninteresting legalism ... to think of our scientific system of the world as involved en bloc in every prediction. More modest chunks suffice, and so may be ascribed their independent empirical meaning, nearly enough, since some vagueness in meaning must be allowed for in any event” (Quine 1960, 71). This admission may be somewhat surprising, and indeed Fogelin (1997) uses it effectively as part of his argument that Quine’s naturalism was of a more limited scope than is commonly understood. The Quineian holistic thesis, it seems, is to be taken with a large grain of salt, as a logically extreme possibility (a “legalism,” albeit an “interesting” one), but in practice we need to limit ourselves to examine only local portions of the web of beliefs at any given time, taking much of the background for granted, at least until further notice.

The other pertinent caveat made explicit by the above quoted passage pertains to Quine’s critique of the logical positivists’ distinction between synthetic and analytic truths that we have just explored. That critique is based on the idea that the distinction (one of the two “dogmas”) deploys terms whose meaning is insufficiently clear. But as Hylton (2010) points out, critics have remarked that Quine’s standards for clarity and adequacy are themselves not clear and possibly artificially high. From the point of view of a web of knowledge, the meaning of the terms used by the logical positivists cannot be understood in isolation, but requires a holistic approach. The problem is that if one pushes holism too far one gives up on the idea of meaning altogether, as Quine himself realized.

From epistemology back to metaphysics. According to Fogelin (1997) Quine began by admitting a fairly broad ontology, but became increasingly committed to physicalism (by about 1953), which was “whole-hearted except for the grudging admission of a few, seemingly unavoidable, abstract entities” (Fogelin, p. 545). Quine did allow — in principle — things like the “positing [of] sensibilia, possibilia, spirits, a Creator,” as long as they carried the same sort of theoretical usefulness as quarks and black holes (Quine 1995, p. 252). Analogously, E. Nagel (1955) wrote that “naturalism does not dismiss every other differing conception of the scheme of things as logically impossible; and it does not rule out all alternatives to itself on a priori grounds” (Nagel 1955, 12). Early on Quine even entertained (and ultimately abandoned) an ontology that used only the set of space- time points, i.e. an ontology of entirely abstract entities, something that nowadays would be considered an extreme form of structural realism of the type defended by Ladyman and Ross (2009; we’ll get back to them later on). Quine went on to articulate what he called a “regimented” theory that contains no abstract objects other than sets (his famous “desert” ontology). As Hylton (2010) points out, however, sets can be used to define a wide range of abstracta, only some of which are acknowledged by Quine (e.g., numbers, functions, and mathematical objects in general). Quine excluded propositions and possible entities from his list of admitted abstracta, on the ground that the identity criteria in the latter cases are “unclear.” But as I mentioned earlier, Quine’s own criteria for including or excluding something from his ontology were themselves not very clear.

The bottom line is that for Quine metaphysics is metaphysics of science, because science is pretty much the only game in town when it comes to grounding our beliefs about reality. It then naturally follows from this position that epistemology is just psychology, as he famously stated, a conclusion that has seen some push back since, as also evidenced by the empirical fact that epistemologists have not migrated en masse into Psychology departments.

It is worth remembering that Quine did not understand scientific knowledge as different from ordinary knowledge (Hylton 2010), which means that his position can be construed as different from blatant scientism (Sorell 1994): the latter is about reducing everything worth investigating to science, so that philosophical questions become either irrelevant or scientific. It would be more accurate to say that for Quine there was little if any distinction between science and philosophy because both, when done correctly, were in turn indistinguishable from (sound) ordinary knowledge. Indeed, he wrote (Quine 1995, 256) “Is this sort of thing still philosophy? Naturalism brings a salutary blurring of such boundaries.” Blurring boundaries is not at all the same as collapsing philosophy into science, as some more aggressive contemporary naturalistic philosophers are either explicitly advocating or implicitly endorsing (e.g., Alex Rosenberg in the first group, and perhaps the more recent writings by Dan Dennett in the second).

However we want to reconstruct Quine’s project — something that as any Quine scholar will readily testify is certainly open to a variety of interpretations — it was supposed to retain the philosophically crucial normative aspect of epistemology: “Naturalistic epistemology ... is viewed by Henri Lauener and others as purely descriptive. I disagree. Just as traditional epistemology on its speculative side gets naturalized into science, or next of kin, so on its normative side it gets naturalized into technology, the technology of scientizing” (Quine 1995, 258). But it is not at all clear on what scientific or technological grounds one can move from descriptive to prescriptive epistemology.

Let me bring up a simple example to make the point a bit more clearly. There is a lot of talk these days about how recent discoveries in cognitive science are rendering the study of philosophically based critical thinking and informal logic obsolete. For instance, experimental psychologists have now documented the existence of a number of ingrained cognitive biases, from the tendency to confuse correlation and causation to the confirmation bias (ignoring evidence contrary to one’s own beliefs and accepting evidence supporting them), and many others. Interestingly, cognitive biases tend to map with well known formal and informal logical fallacies, as they have been analyzed by philosophers and logicians for some time. The difference between the psychologist and the philosopher here is precisely that the first one describes the problem empirically, while the second one prescribes the solution logically. The discoveries made by cognitive science actually make it even more important that one study logic, not less. To argue that the psychology somehow supersedes the philosophy would be like suggesting that since many people are really bad at estimating probabilities (thanks to which phenomenon the gambling industry thrives), therefore we should stop teaching probability theory in statistics courses. On the contrary! It is precisely because, empirically speaking, human beings are so bad at reasoning that one needs to emphasize the prescriptive aspect of theoretical disciplines like probability theory and logic (besides, without the latter two fields, how would psychologists even know that people are getting things wrong?). Depending on how exactly one reads Quine, he may have been perfectly fine with the distinction I have just drawn, but I am worried by some authors being more Quineian than Quine these days, which easily leads not just to a “salutary” blurring of boundaries between science and philosophy, but comes close to an outright selling out or dismissal of the philosophical enterprise (e.g., Rosenberg 2011; some of the literature on experimental philosophy that we will take on in the last chapter).

According again to Hylton (2010), one of Quine’s revolutionary steps was to apply naturalism to naturalism, arguing that the reason to believe that natural science provides us with the best way to understand the world is natural science itself. This may sound like straightforwardly circular reasoning, but it would be so only if one were to look for a “foundation” to the edifice of knowledge. If instead one does away with foundational projects altogether and substitutes them with the concept of a web of belief, one does arrive at an intricate — and I would argue more realistic and useful — picture in which science, philosophy, mathematics, logic and “ordinary knowledge” all grade into each other, and all influence each other. Even so, we have seen earlier that Quine himself did not take the metaphor of a web of belief too far (cfr. his comment on “legalism”). What then emerges from a reasonably moderate reading of the Quineian critique of positivism is that the web of belief is underpinned by a number of partially distinct yet overlapping approaches, the resulting patchwork being reflected in the prima facie distinctions we do make among philosophy, science, mathematics, logic and common knowledge. The blurring of disciplinary boundaries is then salutary because it encourages dialogue and cooperation. But altogether ignoring the existence of such boundaries (blurry as they may be) throws the baby out with the bath water and encourages a rapid slide into scientism. In a sense, for me the best response to a strong reading of Quine is that a scientist (or a mathematician, let alone a common person) would most certainly not recognize Quine’s own writings as scientific (or mathematical, or as instances of common knowledge). But no philosopher — whether he disagrees with Quine or not — would have difficulty in recognizing them as philosophy.

What is naturalism, anyway?

As we have seen, one cannot talk about naturalism in 20th century philosophy (and beyond) without paying dues to Quine’s fundamental, one would almost want to say game changing, influence. And the reason to talk about naturalism at all in the context of the current project is that the “naturalistic turn” in (analytic) philosophy represents a crucial piece of the puzzle of how modern philosophy sees itself and its relationship with science. This, finally, is pertinent to my attempt at understanding how the two fields can be said to make progress, albeit in different senses of the term.

Perhaps not surprisingly, however, a “turn to naturalism” means different things to different people, and that’s even without considering the various outright rejections of naturalism that have been voiced and continue to be voiced by a number of philosophers. Before proceeding, then, I shall make my own position clear: I agree with Ladyman and Ross (2009) when they characterize any philosophy that does not take science seriously as “neo-Scholasticism.” This, given the bad reputation of Scholasticism in contemporary philosophical circles, may seem unduly harsh, but I actually think it hits the nails exactly right. Scholastic philosophers (Kretzman et al. 1982) carried out a lot of logically rigorous work, but their efforts had comparatively limited lasting import precisely because they assumed a number of notions that turned out to have little, if any, scientific traction. It isn’t that the Scholastics were not clever or interesting, once one bought into their basic assumptions about the world; it’s that their basic assumptions about the world were far off the mark, thereby making their philosophy increasingly less relevant in the long run. The difference between the original Scholastics and what Ladyman and Ross term the neo- variety (explicit examples to be found in the first chapter of their book) is that the former did not have the results of the scientific revolution at their disposal, while the latter do. Therefore, to indulge in neo-Scholastic philosophy these days is the result of a willful, and in my mind misguided, rejection of science. As far as I am concerned, therefore, the dilemma standing in the way of modern philosophy is not whether to do without science (that is simply not a viable option anymore, if it ever was), but how exactly to take on board science and whether this means a renunciation of the project of philosophy altogether (as one may read Quine as advocating, at the least implicitly, at times) or rather its modification and amplification along new directions of inquiry (which I happen to think is the most promising path to take).

Let’s go back first to the already mentioned paper by E. Nagel (1955) and his commentary on naturalism. Nagel defines it not in terms of a particular theory of nature, but as a philosophical stand based on two theses: “the existential and causal primacy of organized matter in the executive order of nature” (1955, 8) and the idea that “the manifest plurality and variety of things, of their qualities and their functions, are an irreducible feature of the cosmos, not a deceptive appearance cloaking some more homogeneous ‘ultimate reality’ or transempirical substance” (1955, 9).

Nagel doesn’t commit naturalism to the strong claim that only what is material exists, for instance mentioning exceptions that include modes of action, relations of meaning, plans and aspirations. All these things “exist” in some important sense of the term and yet are not material (though of course they have a material basis, meaning that it is not possible to conceive of any of them without a physical brain getting involved in the process). But what he does explicitly exclude from the naturalistic standpoint are things like “disembodied forces ... immaterial spirits directing the course of events ... the survival of personality after the corruption of the body,” that is, precisely the sort of entities the Scholastics assumed were part and parcel of the fabric of reality.

We have seen when discussing Quine that Nagel explicitly states that naturalism does not exclude other philosophical standpoints by fiat, but that nonetheless naturalism is the one standpoint overwhelmingly favored by the available evidence. That may sound suspiciously circular to critics of naturalism, though. After all, naturalist philosophers rely on the empirical evidence provided by science, and the empirical methods of science themselves assume a naturalistic framework, thereby stacking the deck against any form of non-naturalism.

There actually is a vibrant discussion in current philosophy of science about the extent to which science is automatically committed to philosophical naturalism, with people like Pennock (2011) forcefully arguing that it is, and others (Boudry 2013) responding with arguments that are very much in line with Nagel’s early insight. For the latter the logical- empirical method does not a priori exclude non-naturalistic phenomena, as long as they make some kind of contact with empirically verifiable reality: “There must be some connection between the postulated character of the hypothetical trans-empirical ground, and the empirically observable traits in the world around us; for otherwise the [non- naturalistic] hypothesis is otiose, and not relevant to the spatio-temporal processes of nature” (p. 13). Or to put not too fine a point on it: otherwise we return to full fledged Scholasticism. The basic idea, therefore, is not that naturalism excludes, say, transcendental feelings or mystical experiences a priori, but rather that a naturalist will not treat those feelings and experiences as any kind of evidence of a transcendental realm. They are far more parsimoniously interpreted as byproducts of the way in which the human brain responds to certain physical-chemical conditions (like stress, self-imposed abstinence from food, deep meditation or prayer, exposure to hallucinatory substances, and so on).

Two authors who have more recently commented insightfully on naturalism in philosophy are Laudan (1990) and Maffie (1995). Since their comments speak more closely to Quine’s concerns about the relationship between science and philosophy, and in particular about the status of epistemology, they are especially relevant to my project here. Laudan recognizes that “naturalism” actually refers to a variety of positions, but that “on the intellectual road map, naturalism is to be found roughly equidistant between pragmatism and scientism” (1990, 44). He then immediately moves to the issue of epistemology: “Epistemic naturalism ... holds that the claims of philosophy are to be adjudicated in the same ways that we adjudicate claims in other walks of life, such as science, common sense and the law ... it holds that the theory of knowledge is continuous with other sorts of theories about how the natural world is constituted” (1990, 44).

Pausing for a moment here, we can recognize that Laudan’s position is in important respects analogous to Quine’s. Recall from our discussion above that for Quine too there is no fundamental, qualitative difference between the way in which scientists and philosophers operate epistemically, and indeed there is no difference between either of those and the way in which rational human beings operate either. In fact, it would be bizarre if philosophers (or scientists, for that matter) could claim some special power of insight into the world that nobody else has access to (that would make them mystics, I suppose). But I think that agreeing that philosophy is sufficiently distinct from science (and both are distinct from commonsense) simply does not require such an extreme view, as both Laudan and Maffie clearly articulate. Neither of these authors, then, agrees wholeheartedly with Quine’s attempt to almost erase such distinctions. Laudan in particular refers to Quine’s view of methodological strategies as “Spartan,” being essentially limited to a combination of hypothetic-deductivism and the principle of simplicity. Laudan goes on to say that there is a place for normative considerations in a naturalized epistemology, which for him implies that epistemology does not simply reduce to psychology. While Quine was inclined to think of the decision to give up any philosophical claims to prescriptive epistemology as boldly biting the naturalistic bullet, Laudan counters that it is “more akin to using that bullet to shoot yourself in the foot” (1990, 46), a sentiment — I must admit — that has often accompanied my own readings of Quine. Laudan suggests instead that a “thoroughly naturalistic approach to inquiry can, in perfectly good conscience, countenance prescriptive epistemology, provided of course that the prescriptions in question are understood as empirically defeasible.” (1990, 46). The basic idea, I take it, is that epistemologists can continue in good conscience, qua philosophers, to do what they have always done: critically reflect on the various means to acquire and verify knowledge; and they can keep writing prescriptively (as in “this and that are good/sound epistemic practices; those and others are bad/unsound practices”), as long as they are willing to revise their positions whenever pertinent empirical evidence comes their way. But at its best philosophy has always been able to incorporate and reflect on pertinent empirical evidence, without doing so somehow turning it into a straightforward (in this case cognitive) science.

Maffie (1995) mounts yet another reasonable defense of naturalistic philosophy — one that can be read, again, as a reaction to Quine — against what he refers to as “the fallacy of scientism.” Maffie’s model is one of “weak continuity” between epistemology and science. The basic idea is to deny a number of misguided tenets about epistemology: i) that it employs norms and standards that are somehow “higher” than those of science; ii) that it uses a priori methods of evidence of a special kind; iii) that it proceeds in a way that makes no use of the findings of science; iv) that it yields firmer epistemic results than science; and v) that it is somehow prior to any science. All of the above while at the same time affirming that epistemology does employ evidential concepts, norms and goals distinct from those of science. How does Maffie manage to accomplish that?

He puts it this way: “that there is no epistemologically higher or firmer ground than science from which to criticize science does not entail that there is no epistemologically independent ground from which to criticize science” (1995, 4). That is, while defending the old fashioned model of philosophy somehow hovering above all other fields of human knowledge — including science — is untenable, it is simply not the case that the only other available model is the Quine-inspired one of subsuming philosophy into science. Maffie’s suggestion is similar to Laudan’s in this respect: philosophy can (should) keep using its standard tools — like conceptual analysis, “intuition” and reflective equilibrium (more on all these and others near the end of this book) — as long as they are not aloof but integrated with “a posteriori” practices (i.e., squared with the pertinent factual evidence). To put it differently, while for Maffie scientistically oriented naturalist philosophers elevate practicing scientists to a model to be emulated for how to do philosophy in general and epistemology in particular, weak continuity naturalists “look to the critical practices of reflective human beings” more broadly construed (1995, 4). This leads to a view of epistemology as a parallel, independent discipline that can (and should) analyze and when necessary criticize the claims made by science. Science does not get, to put it as Maffie does, “both the only say and the final say” (1995, 19).

Finally, we need to consider yet another way of approaching the issue of naturalism in philosophy, and that’s the distinction — the implications of which have been surveyed by Papineau (2007) — between ontological and epistemological naturalism. [13] Beginning with ontological naturalism, the basic idea is that a modern account of causality has to be rooted in scientific concepts, thus excluding, for instance, the old philosophical possibility of mental causation as a distinct category from its physical counterpart, a la Descartes. Since biological, “mental” and social phenomena all cause physical effects in the world, those effects have to fall within the limits imposed by a scientific understanding of causality. This doctrine is sometimes referred to as the principle of “causal closure” (e.g., Vicente 2006), which in its broadest formulation essentially says that any physical effect must have a physical cause. Of course, even if one accepts the principle of causal closure, there is still room for a varied ontology of the world that includes “objects” that do not per se have physical effects, such as mathematical, modal and possibly normative claims.

Echoing the comments from Nagel (1955) that I have examined above, Papineau points out that naturalism is not a rigid a priori doctrine (something to which naturalists are often accused of adhering to), because it has changed through time in response to the best scientifically informed understanding available. For instance, Descartes-style “interactive dualism” seemed dead for a while, as Leibniz concluded, but became again a live option with Newtonian mechanics and the concept of action at a distance. As is well known, it has lost viability again since then, but one cannot exclude yet another comeback, as remote as that possibility seems at the moment.

A more nuanced question is that of the relationship between naturalism and physicalism. Papineau agrees that there is room for debate here (and so does Fodor, in his influential paper on special sciences: 1974). For instance, although naturalism requires that if a mental state (say, anger) has physical consequences, that mental state has to be the result of physical processes, stronger claims like the one made by type-identity theorists in philosophy of mind (Rosenthal 1994), that thinking about a number is identical with a particular physical property of your brain, go too far and are in fact implausible because different brains could produce similar thoughts by different physical routes (an idea referred to as multiple realizability). Which raises the mandatory issue of supervenience: “Non-physical properties should metaphysically supervene on physical properties, in the sense that any two beings who share all physical properties will necessarily share the same non-physical properties, even though the physical properties which so realize the non- physical ones can be different in different beings” (Papineau 2007). The important point to take home here is that a modern naturalistic philosophy is, in this framework, a philosophy that is committed to a broad (and revisable) understanding of ontological naturalism. An equally interesting discussion pertains the type and scope of methodological naturalism. Here Papineau draws a sharp contrast between methodological naturalists who see no fundamental difference between science and philosophy (again, a la Quine), and methodological “anti-naturalists” who do (as, I imagine, anyone strongly opposed to the approach characteristic of analytic philosophy). I think he is a bit too quick here, as a model along the lines of what Maffie calls “weak continuity” makes more sense to me. Indeed, Papineau immediately softens the allegedly sharp dichotomy: “even those philosophers who are suspicious of science must allow that philosophical analyses can sometimes hinge on scientific findings — we need only think of the role that the causal closure of physics ... play[s] in the contemporary mind-body debate. And, on the other side, even the philosophical friends of science must admit that there are some differences at least between philosophy and natural science — for one thing, philosophers characteristically do not gather empirical data in the way that scientists do.” I think the latter is still too weak, since it’s not just that philosophers do not gather empirical data (besides, see my discussion of so-called “experimental philosophy” in the last chapter of this book), it’s that the concerns, tools, and attitudes of philosophers qua philosophers are partially distinct from those of scientists qua scientists.

Again, it is Papineau himself that provides reasonable ammunition for a weak continuity view of the relationship between science and philosophy: “Think of topics like weakness of will, the importance of originality in art, or the semantics of fiction. What seems to identify these as philosophical issues is that our thinking is in some kind of theoretical tangle, supporting different lines of thought that lead to conflicting conclusions. Progress requires an unravelling of premises, including perhaps an unearthing of implicit assumptions that we didn’t realise we had, and a search for alternative positions that don’t generate further contradictions. Here too empirical data are clearly not going to be crucial in deciding theoretical questions — often we have all the data we could want, but can’t find a good way of accommodating them” (Papineau 2007).

Those last few sentences, I think, really get to the heart of the matter. First off, notice the unabashed (and welcome!) acknowledgment that philosophy does, in fact, make progress. Second, Papineau points out that philosophical problems are characterized by a type of interesting empirical underdetermination: if an issue can be settled entirely on empirical grounds, then it squarely belongs to science and philosophers have very little business butting in. Third, and by the same token, philosophical discussions are not going to be independent of science-provided empirical evidence, on penalty of falling back once more into neo-Scholasticism. Lastly, Papineau sees, and I agree, philosophy’s goal (or at least one of philosophy’s goals) as that of conceptual analysis and clarification. That’s because the best philosophy is based on an effective deployment of formal and informal logic, it is a way of thinking and reflecting about issues, not a way of gathering empirical data about those issues.

Having laid out so far the bases for a reconstruction of the nature and tools of philosophy, over the next two chapters we will move to briefly examine different examples of progress in fields that bear distinct types of resemblances to philosophy: science — often, and justly, seen as the paragon of a progressive field; mathematics — which equally uncontrovertibly presents us with a picture of progress, perhaps even more clearly so than in science, and yet where progress is achieved by substantively different means; and logic — where progress has certainly occurred, but in a way that is distinct from (if similar to) the one characterizing math. We will then move to the crucial issue of whether and how philosophy itself makes progress, by way of an analysis of three specific areas of philosophical inquiry.

4. Progress in Science

“The wrong view of science betrays itself in the craving to be right; for it is not his possession of knowledge, of irrefutable truth, that makes the man of science, but his persistent and recklessly critical quest for truth.”
(Karl Popper)

If there is one area of human endeavor where there seems to be no doubt that the concept of progress applies, that surely must be science. Indeed, more often than not, as we have seen, it is prominent scientists who hurl accusations of uselessness to philosophy precisely based on what I think is a profoundly misguided comparison between the two disciplines, where the (alleged) lack of progress in philosophy is contrasted with the (unquestioned) steady progress of science.

As we shall see in this chapter, however, it is not immediately clear exactly in what sense science makes progress, or how precisely we are to measure such progress. Not surprisingly, it is philosophers of science — together with historians and sociologists of the discipline — who have investigated some of the basic assumptions about the practice of science that (most) scientists themselves simply take for granted. And such probing has been going on since at the least the beginning of the last century, with interesting results.

Just to make things as clear as possible from the outset, I do not deny that science makes progress, in something like the way in which scientists themselves (not to mention the public at large) think it does. My goal here is to show that even so, it is surprisingly difficult to cash out an unambiguously clear picture of what this means, and to explore a number of alternative philosophical accounts of the nature of scientific knowledge. While this is not a book on the philosophy of science, and hence I will have to limit myself to only sketches of a number of complex and nuanced positions while pretty much ignoring others for the sake of brevity, it is important to go through this exercise for two reasons: first, because it should bring about some humility on the part of scientistically inclined people (or so one can hope); second, because it will put into better perspective the reasons why arguing that philosophy in turn makes progress is both not straightforward and yet perfectly plausible.

The obvious starting point: the Correspondence Theory of Truth

Every scientist I have talked to about these matters (though, of course, systematic sociological research on this would be welcome!), has implicitly endorsed what philosophers refer to as the Correspondence Theory of Truth (CToT: David 2009). This also likely captures the meaning of truth that lay people endorse, and may be at the roots of the almost universal belief that science makes progress, specifically in the sense of discovering true things about the world (or — in a somewhat more sophisticated fashion — of producing a series of theories about the nature of the world that come closer and closer to the truth). Interestingly, many philosophers up until recently have also endorsed the CToT, and have done so without even bothering to produce arguments in its favor, since it has often been taken to be self-evident. For example, Descartes (1639 / 1991, AT II 597) famously put it this way: “I have never had any doubts about truth, because it seems a notion so transcendentally clear that nobody can be ignorant of it ... the word ‘truth,’ in the strict sense, denotes the conformity of thought with its object.”

Still, what, exactly, is the CToT? Here is how Aristotle put it (350 BCE, 1011b25): “To say of what is that it is not, or of what is not that it is, is false, while to say of what is that it is, and of what is not that it is not, is true.” Not exactly the most elegant rendition of it, but a concept that we find pretty much unchanged in Aquinas, Descartes, Hume, Kant and several other medieval and early modern writers. Its contemporary rendition dates to the early days of analytic philosophy, and particularly to the work of G.E. Moore and Bertrand Russell. Truth, according to the CToT, is correspondence to facts: to say that statement / theory X is true just means that there is a factual state of affairs Y in the world that is as described by X. It seems pretty straightforward and hard to dispute, and yet much 20th century philosophy of science and epistemology has done just that: dispute the CToT with the aim of carefully unpacking the notions on which it is based, and — if warranted — to replace it with a better theory of truth.

The first problem lies in the very use of the word “truth.” It seems obvious what we mean if we say that, for instance, it is true that the planet Saturn has rings in orbit around its center of gravity. But it should be equally obvious what we mean when we say things like the Pythagorean theorem is true (within the framework of Euclidean geometry). And yet the two senses of the word “truth” here are quite distinct: the first refers to the sort of truth that can be ascertained (insofar as it can) via observation or experiment; the second one refers to truth that can be arrived at by deductive mathematical proof. We can also say that the law of the excluded middle — which says that either a proposition or its negation are true, but not both — is (logically) true within the framework of classical logic. This is related to, and yet somehow distinct, from the sense in which the Pythagorean theorem is true, and of course it is even further distinct from the business about Saturn and its rings. There are yet other situations in which we can reasonably and more or less uncontroversially say that something is true. For instance, according to every ethical system that I am aware of it is true that murdering someone is wrong. More esoterically, philosophers interested in possible world semantics and other types of modal logic (Garson 2009) may also wish to say that some statement or another is “true” of all nearby possible worlds, and so on.

The bottom line is that the concept of truth is in fact heterogeneous, so that we need to be careful about which sense we employ in any specific instance. Once appreciated, this is not an obstacle unless a scientistically inclined person wants to say, for instance, that moral truths are the same kind of truths as scientific ones. As you may recall, we have in fact encountered a number of such cavalier statements already, which reinforces the point that the apparently obvious differences among the above mentioned meanings of truth do, in fact, need to be spelled out and constantly kept in mind. So, I will limit application of the CToT — within the specific context that interests us here — to empirical-scientific truths about the way the world is and works. It is of course the case that mathematicians, and even some ethicists, deploy a version of it within their respective domains of interest, but I hope it is uncontroversial that in those cases we are talking about a different type of “correspondence” (i.e., not one that can even in principle be verified by observation or experiment) — and this quite apart from my personal skepticism of mathematical Platonism (see Introduction) or of moral realism (which I will leave for another time). (For a classic, sophisticated discussion of mathematical truth taking account of the Platonist perspective see: Benacerraf, 1973.)

Even if we agree that the CToT in science makes intuitive sense if we limit ourselves to a restricted meaning of the word “fact,” we still need to examine a number of objections and alternative proposals to the theory, as they will help appreciate why to talk about progress in science is not quite as straightforward as one might think. There are several issues that have been raised about the soundness of the CToT (see David 2009 for a survey and further references), one of which is that it simply does not amount to a “theory” of any sort; in fact, it has been characterized as a trivial statement, a vacuous platitude, and so forth. This is somewhat harsh, and even if the CToT really is not anything that one might reasonably label with the lofty term of “theory” it doesn’t mean that it is either trivial or vacuous. One way to think of it is that the CToT is closer to a working definition of what truth is, particularly in science (some philosophers, like David, refer to these situations as “mini-theories”). And definitions are useful, if not necessarily explanatory, as they anchor our discussions and provide the starting point for further exploration. [14]

Perhaps a more serious objection to the CToT is that it relies on the much debated concept of “correspondence,” which itself needs to be unpacked (the classical reference here is Field (1972), but see also Horwich 1990). To simplify quite a bit, one of the possible answers is that defenders of the CToT can invoke the more precise (at least in mathematics) idea of isomorphism as the type of correspondence they have in mind. The problem is that — unlike in math — it is not at all straightforward to cash out what it means to say that there is an isomorphism between a scientific theory (which is formulated in the abstract language of science) and a physical state of affairs in the world. This is a good point, but as David (2009) retorts, this sort of problems holds for any type of semantic relation, not just for isomorphisms in the context of the CToT.

Another way to take the measure of the CToT is to look at some of its principal rivals, as they have been put forth during the past several decades. One such rival is a coherentist approach to truth (Young 2013), which replaces the idea of correspondence (with facts) with the idea of coherence (among propositions). This move works better, I suspect, for logic and mathematics (where internal coherence is a primary standard), but less so for scientific theories. There are simply too many possible theories about the world that are coherent and yet do not actually describe the world as it is (or as we understand it to be) — a problem known in philosophy of science as the underdetermination of theory by the data, and one that from time to time actually plagues bona fide scientific theories, as it is currently the case with string theory in physics (Smolin 2007).

A second set of alternatives to the CToT is constituted by a number of pragmatic theories of truth, put forth by philosophers like Peirce and James (see Hookway’s (2008) refinement of Peirce’s original account). Famously, these two authors differed somewhat, with James interested in a pluralist account of truth and Peirce more inclined toward a concept that works better for a realist view of science. For Peirce scientific (or, more generally, empirical) investigation converges on the truth because our imperfect sensations are constrained by the real world out there, which leads to a sufficiently robust sense of “reality” while at the same time allowing us to maintain some degree of skepticism about specific empirical findings and theoretical constructs. Here is how Peirce characterizes the process (Peirce, 1992 & 1999, vol. 1, 138):

“So with all scientific research. Different minds may set out with the most antagonistic views, but the progress of investigation carries them by a force outside of themselves to one and the same conclusion. This activity of thought by which we are carried, not where we wish, but to a foreordained goal, is like the operation of destiny. No modification of the point of view taken, no selection of other facts for study, no natural bent of mind even, can enable a man to escape the predestinate opinion.”

For Peirce, therefore, truth is an “opinion” that is destined to be agreed upon (eventually) by all inquirers, and the reason for this agreement is that the object of such opinion is reality. This is actually something that I think scientists and realist-inclined philosophers could live with. James’ views, by contrast, are a bit more controversial and prima facie less science friendly, for instance when he claims that truth is whatever proves to be good to believe (James 1907/1975, 42), or when he defines truth as whatever is instrumental to our goals (James 1907/1975, 34). James did qualify those statements to the effect that they are meant in the long run and on the whole (James 1907/1975, 106), thus invoking a concept of convergence toward truth that is not too dissimilar from Peirce’s. Still, by this route James arrived at his famous (and famously questionable) defense of theological beliefs: belief in God becomes “true” because “[it] yield religious comfort to a most respectable class of minds” (James 1907/1975, 40). While Hookway (2008) suggests that Bertrand Russell was a bit unfair to James when he said that the latter’s theory of truth committed him to the “truth” that Santa Claus exists, Bertie may have had a point.

There are a number of other alternatives to the CToT that need to be at the least briefly mentioned. For instance, the identity theory says that true propositions do not correspond to facts, they are facts. It is not crystal clear in what ontological sense this is the case. Then we have deflationist approaches to truth: according to the CToT, “Snow is white” is true iff it corresponds to the fact that snow is white; for a deflationist, however, “Snow is white” is true iff snow is (in fact) white. The move basically consists in dropping the “corresponds to” part of the CToT. David (2009), however, points out that many CToT statements are not so easily “deflated”; moreover, this particular debate seems to hinge on issues of semantics rather than on any “theory” of what it is for something to be true.

A position that gathers more of my sympathies is that of alethic pluralism, according to which truth is multiply realizable. As David (2009) puts is: “truth is constituted by different properties for true propositions from different domains of discourse: by correspondence to fact for true propositions from the domain of scientific or everyday discourse about physical things; by some epistemic property, such as coherence or superassertibility, for true propositions from the domain of ethical and aesthetic discourse, and maybe by still other properties for other domains of discourse.” This in a sense closes the circle, as alethic pluralism conjoins our discussion of theories of truth with my initial observation that “facts” come in a variety of flavors (empirical, mathematical, logical, ethical, etc.), with distinct flavors requiring distinct conceptions of what counts as true.

The goal of this brief overview of theories of truth was to establish two points: first, contra popular opinion (especially among scientists), it is not exactly straightforward to claim that science makes progress toward truth about the natural world, in part because the concept of “truth” itself is fraught with surprising difficulties; second, and relatedly, there are different conceptions of truth, some of which represent the best we can do to justify our intuitive sense that science does indeed make progress in the teleonomic sense of approaching truth, and others that may constitute a better basis to judge progress (understood in a different fashion, along the lines of our discussion in the Introduction) in other fields — such as mathematics, logic, and of course, philosophy.

Progress in science: some philosophical accounts

I now turn to some philosophical considerations about progress in science. The literature here is vast, as it encompasses large swaths of epistemology and philosophy of science. Since what you are reading is not a graduate level textbook in philosophy of science, I will focus my remarks primarily on some recent overviews of the subject matter by Niiniluoto (2011, an expansion and update of Niiniluoto 1980) and Bird (2007, 2010), because they capture much of what I think needs to be said for my purposes here. Niiniluoto (2011) in particular will offer the interested reader plenty of additional references to expand one’s understanding on this issue beyond what is required in this chapter. Readers with a more general (i.e., less technical) interest in the history of ideas in philosophy of science should consult the invaluable Chalmers (2013). There are many other excellent sources and interesting viewpoints out there, however, and I will address some of them as needed throughout the remainder of this discussion.

A good starting point for conceptual analyses of progress in science is to trace their roots back a few centuries, particularly the period between the Renaissance and the Enlightenment, when people began to take seriously the idea that “natural philosophy” was a new and potentially very powerful kid on the block when it came to the augmentation of human knowledge and understanding. The simplest view had been held by scientists themselves since at least the 17th century (e.g., Robert Boyle and Robert Hooke), and according to Niiniluoto (1980) can be traced back to the 15th century and Nicholas of Cusa’s concept of “learned ignorance”: science makes progress because it accumulates truths about the world (what I have been calling the “teleonomic” account).

But philosophers, beginning as early as the 18th century, pointed out that this assumes a rather optimistic (some would even say naive) view of the epistemic powers of science. Nonetheless, the optimistic attitude endured through the Enlightenment (particularly via Auguste Comte’s positivism) and led to familiar positions, such as this one by Sarton (1936): “progress has no definite and unquestionable meaning in other fields than the field of science.” As we have seen earlier in the book, I know a number of scientists who still happily subscribe without much qualification to Sarton’s take on the matter.

By the 19th century, however, some philosophers were beginning to articulate more nuanced or qualified perspectives, while still maintaining that scientific progress is to be understood as an accumulation of knowledge about the world (and, since according to the standard account of knowledge, the latter is equivalent to justified true beliefs, this means that science accumulates truths about the world) [15]. We have previously encountered, for instance, Charles Peirce’s pragmatic take on truth, which led him to think of it as the limit — in a mathematical sense — of scientific inquiry: “We hope that in the progress of science its error will indefinitely diminish, just as the error of 3.14159, the value given for π, will indefinitely diminish as the calculation is carried to more and more places of decimal” (Peirce, quoted in Niiniluoto, 1980, 432). The analogy, however, is problematic for a variety of reasons, a main one being that it can be convincingly argued that there is no reason to think we have any guarantee of monotonic convergence in scientific knowledge, while there is in mathematical knowledge, at least in the case of relatively simple mathematical problems, such as the calculation with ever increasing degrees of accuracy of the digits of π.

Parenthetically, it is interesting to consider a perennial side discussion related to the idea of scientific progress: if science does make progress, will it eventually come to an end? Science journalist John Horgan (1996) got into trouble when he asked a number of scientists (and philosophers!) that very question, since many scientists apparently just refuse to take it (or the idea of limits to scientific knowledge) seriously. Indeed, according to Niiniluoto (1980, 434), already astronomer John Herschel is on record has having stated, back in 1831: “[the world is an] inexhaustible store which only awaits our continued endeavors,” although George Gore argued the opposite in 1878, on the ground that we will either have solved all problems worth solving, or we will run out of technical and epistemic resources. I tend to agree with Gore rather than Herschel, but the point is that the very question implies some account of how science actually progresses. If there is no progress, then it is harder to see in which sense one can meaningfully ask if the process will reach an end.

The debate on how exactly science makes progress really took off in philosophy of science in the ‘60s and ’70, particularly with the contributions of Popper, Kuhn, and Feyerabend. Setting aside the latter’s “radical” epistemology (according to which there is no such thing as scientific methodology, anything goes as long as it delivers whatever results we are after), a major distinction can be drawn between Popper’s and Kuhn’s views (e.g, Rowbottom 2011). In Popper’s view scientific progress results from a continuous approximation to the truth, achieved via falsification of previously held theories. This was part of Popper’s well known attempt at overcoming Hume’s problem of induction, which led him to rethink the scientific approach in terms of falsification rather than confirmation (because confirmation of theories is too easy to achieve, and does not even separate science from pseudoscience: Pigliucci and Boudry 2013). Popper’s views, however, run afoul of the well known Duhem-Quine problem, which we have already discussed.

Kuhn famously framed the issue of progress in science in a more neutral fashion. Indeed, so neutral that he was quickly accused of advancing a framework that makes it impossible to actually talk about scientific progress, lending him accusations of relativism, which he vigorously rejected late in his career (Kuhn 1982). Kuhn’s view was that we can easily make sense of progress within a given paradigm: during the so-called “puzzle solving” phase of scientific discovery scientists deploy the conceptual and instrumental tools made available by the reigning paradigm to solve a number of local problems (“puzzles”). The more problems are thus solved, the more one can say science is making (local) progress. According to Kuhn, however, at some point there will be a sufficiently high number of unsolved puzzles, which will lead to a crisis of confidence in the paradigm and eventually to its replacement by a new paradigm. What is difficult to say — and even Kuhn himself had a hard time articulating it — is in what sense moving from one paradigm to the other counts as progress. In fact, Kuhn’s famous analogy between paradigms and gestalt switches in the psychology of perception (those cases where the same image can be interpreted in completely different ways by the brain) did not help, since the two alternative perceptions of a gestalt image have equal claim to be the “correct” interpretation (worse: neither one, technically, is correct since the images are designed on purpose in order to be ambiguous). Kuhn really did sound at some point as if he were saying that paradigms are convenient frameworks for doing science, with no way to determine whether and in what sense a given paradigm may be better than another one.

Moreover, things get apparently worse for a Kuhnian view of scientific progress because of the existence of what are usually referred to as “Kuhn losses.” These are instances where puzzles that were solved under the old paradigm reemerge as problematic under the new one. For instance, the old phlogiston theory in physics accounted for why metals have similar properties (they all contain phlogiston). Except that it turned out that there is no such thing as phlogiston, so the problem was reopened (and solved again, in terms of modern atomic theory). Kuhn losses open up the possibility of scientific regress, at least locally. A number of issues immediately present themselves once we start looking at scientific progress this way. To begin with, what exactly counts as a “problem” or “puzzle”? Depending on how we answer this question — which at the very least is bound to be specific to subfields of the natural sciences — our estimate of Kuhn losses may vary dramatically. Also, as much as the Kuhnian broad view can be taken to be neutral with respect to the issue of progress in science, certainly it will be difficult to talk about solving puzzles without any reference to concepts such as truth or truth-likeness, so that again we arrive at least at a minimalist view of progress. Ultimately, it is an issue for historians of science to determine the relative frequency of Kuhn losses, and it may turn out to be the case that their numbers are much smaller compared to the number of new puzzles that are solved after a paradigm shift, so that a meaningful — even quantifiable — sense of progress in science could be recovered even within a Kuhnian framework.

Kuhn himself became quickly aware of these issues, and attempted to articulate a positive view of progress in science in his famous Postscript to the last edition of The Structure of Scientific Revolutions. There he does three things to clarify his position and respond to his critics: he argues that philosophy of science is both prescriptive and descriptive, so that any accusation that he mixed up the two roles is beside the point. He also spent a significant amount of time elaborating on his central concept of “paradigm,” re-defining it as a disciplinary matrix that includes not just whatever dominant scientific theory holds the field in a given area of inquiry (e.g., Newtonian mechanics, or general relativity), but also the ensemble of accepted experimental and analytical methods, ancillary concepts and hypotheses, what counts as relevant or important questions that remain to be addressed, and even the type of training for graduate and undergraduate students, which is the way the new generation of scientists is introduced to the dominant paradigm. Crucially for my discussion here, however, what Kuhn also attempted in the Postscript was a defense of the idea of progress in science. That defense was only partial: he used the metaphor of an evolutionary tree of scientific ideas and suggested that science progresses along the unfolding of new theories, which branch out of old ones. But he also admitted that he was a “relativist” in the narrow sense that he didn’t believe that scientists can meaningfully talk about reality “out there” in a theory-independent fashion. Given its importance and influence on all subsequent discourse, it is worth quoting that passage in full here:

“Imagine an evolutionary tree representing the development of the modern scientific specialties from their common origins in, say, primitive natural philosophy and the crafts. A line drawn up that tree, never doubling back, from the trunk to the tip of some branch would trace a succession of theories related by descent. Considering any two such theories, chosen from points not too near their origin, it should be easy to design a list of criteria that would enable an uncommitted observer to distinguish the earlier from the more recent theory time after time. Among the most useful would be: accuracy of prediction, particularly of quantitative prediction; the balance between esoteric and everyday subject matter; and the number of different problems solved. Less useful for this purpose, though also important determinants of scientific life, would be such values as simplicity, scope, and compatibility with other specialties. Those lists are not yet the ones required, but I have no doubt that they can be completed. If they can, then scientific development is, like biological, a unidirectional and irreversible process. Later scientific theories are better than earlier ones for solving puzzles in the often quite different environments to which they are applied. That is not a relativist’s position, and it displays the sense in which I am a convinced believer in scientific progress.”

“Compared with the notion of progress most prevalent among both philosophers of science and laymen, however, this position lacks an essential element. A scientific theory is usually felt to be better than its predecessors not only in the sense that it is a better instrument for discovering and solving puzzles but also because it is somehow a better representation of what nature is really like. One often hears that successive theories grow ever closer to, or approximate more and more closely to, the truth. Apparently generalisations like that refer not to the puzzle-solutions and the concrete predictions derived from a theory but rather to its ontology, to the match, that is, between the entities with which the theory populates nature and what is ‘really there.’”

“Perhaps there is some other way of salvaging the notion of ‘truth’ for application to whole theories, but this one will not do. There is, I think, no theory-independent way to reconstruct phrases like ‘really there’; the notion of a match between the ontology of a theory and its ‘real’ counterpart in nature now seems to me illusive in principle. Besides, as a historian, I am impressed with the implausibility of the view. I do not doubt, for example, that Newton’s mechanics improves on Aristotle’s and that Einstein’s improves on Newton’s as instruments for puzzle-solving. But I can see in their succession no coherent direction of ontological development. On the contrary, in some important respects, though by no means in all, Einstein’s general theory of relativity is closer to Aristotle’s than either of them is to Newton’s. Though the temptation to describe that position as relativistic is understandable, the description seems to me wrong. Conversely, if the position be relativism, I cannot see that the relativist loses anything needed to account for the nature and development of the sciences.” (Kuhn, 2012, 204-205)

It is in the context of both Popper and Kuhn that our next quick entry makes sense: Imre Lakatos’ (1963/64, 1970) idea of scientific research programmes. Lakatos (a student of Popper) sought to overcome the opposition between what he saw as the logicist approach put forth by his mentor and the more psychological take elaborated by Kuhn, while retaining advantages of both. He therefore suggested that science does make progress, but via what he called research programmes. These are the Lakatosian equivalent of Kuhn’s paradigms, and therefore much broader than the specific theories that Popper discussed in terms of falsification. Research programs are made of a “hard core” and a “protective belt”: the first is comprised of whatever theoretical commitment would, if abandoned, essentially spell the end of the programme itself; the second one includes “expendable” ancillary hypotheses or theoretical constructs which, if abandoned, would not trigger a Kuhnian crisis. For instance, part of the hard core of the Copernican theory was the idea that the Earth rotates around the Sun, not the other way around. However, Copernicus’ initial assumption that the orbits of the planets are circular was part of the protective belt. When that particular idea was abandoned, by Kepler — who realized that the orbits must be elliptical instead — the theory survived, and the programme kept being, in Lakatos’ terminology, “progressive,” meaning that it led to further research and discovery. Nevertheless, sometimes research programmes do run into significant problems, and have to rely on their protective belt in an increasingly ad hoc fashion, precisely the sort of thing that Popper would have said would doom any serious scientific theory. Before Copernicus, for instance, the Ptolemaic system had to be supplemented with an increasing number of (entirely imaginary, as it turned out) epicycles in order to keep it in reasonable, though still inaccurate, working order.

Thanks to the Popper-Kuhn-Lakatos debates of the 1960s and ‘70s, then, philosophers of science arrived at an understanding of a number of ways in which science can be said to be progressive, from the more cautious one put forth by Kuhn above, to the more Popperian (in spirit) version elaborated by Lakatos. Let me now jump to some of the more recent literature (Niiniluoto 2011), where a distinction is made between progress of science in the axiological (i.e., normative) sense and more neutral descriptions, such as “development.” To simplify a bit, the basic idea is that scientists and philosophers are concerned with the axiology of the scientific enterprise, while sociologists and historians of science tend to take a descriptive approach, although it seems that no project aiming at understanding such a complex set of issues can do without some congruence between descriptive and prescriptive undertakings — just like Kuhn had suggested in his Postscript.

We can usefully conceptualize much contemporary philosophical discourse on scientific progress following a simple classification proposed by Bird (2007): progress can be thought of in an epistemic, functionalist, or semantic key. From an epistemic perspective (the one that Bird himself favors), scientific progress is cashed out as accumulation of (scientific) knowledge; functionally, progress is defined in terms of a particular function, as in the case of Kuhn’s (and, later, Larry Laudan’s 1981a) problem solving ability, as we have already seen; semantically, progress is an issue of increasing verisimilitude, as was proposed by Popper and has been articulated in more detail recently by Niiniluoto. We have already explored the functionalist approach to some extent, so I will now focus on Bird’s epistemic take and Niiniluoto’s semantic one, though discussing both of them will require going back to Kuhn-Laudan style functionalism as a useful contrast.

Bird’s epistemic account assumes the standard (if controversial among epistemologists) definition of knowledge as justified true belief, of which scientific knowledge is a particular subset. That is because Bird — correctly — wants to avoid counting as knowledge instances in which one arrives at the right conclusion by sheer luck. In this sense, Bird simply continues a long tradition in philosophy of science according to which the discipline is concerned with the context of justification of scientific theorizing, as opposed to the context of scientific discovery, which is best left to the field of cognitive psychology. (This straightforward separation between the two contexts has been challenged since Quine, as we have seen in the previous chapter, but we will maintain it as a first approximation for the purposes of this discussion.)

Bird (2010) provides this historical example as a nice episode illustrating how scientific knowledge accumulates by way of a continuous interplay between evidence and theory: “In the context of the debate between Millikan and Ehrenhaft over whether there is a single basic unit of electrical charge, the unique charge of an electron, Millikan’s experimental data are the evidence that helps establish the truth of the theory that electrons all have the same charge, with a value of 4.8 × 10−10 esu. In the context of assessing evidence relevant to the standard model of particle physics, these latter propositions are considered as evidence not as hypotheses.” Notice here that Bird deploys an understanding of the fact that there is no sharp difference between observation and hypothesis, with the notion that electrons have uniform charge shifting from the first to the second status depending on the theoretical context. Indeed, Bird goes on to discuss cases in which the very category of “observation” is actually quite fuzzy, as when we consider weather models, where a good chunk of the “observations” is actually constituted by the output of processing of raw data collected by automated stations and put through the filter of sophisticated computer algorithms — all without direct human intervention, and pretty removed from the everyday meaning of the term “observation.”

All of this to acknowledge that Bird’s account is anything but naive, and yet is affected by a couple of issues. One is its reliance on the already mentioned conception of knowledge as justified true belief (which in turn hinges on some version of the correspondence theory of truth, typically rejected by functionalists like Kuhn and Laudan). Another — more subtle — one is sometimes referred to as the problem of unconceived alternatives (Devitt 2011). Science is a human activity, and as such it is severely limited by the epistemic constraints inherent in being human, including the fact that at any given time scientists may simply not have thought of a good enough alternative theory (not to mention of the best theory) for any particular problem, and we have no way to know this if not a posteriori, from a historical perspective. Another way to put this is that scientists, at any particular point in time, mostly have access to “conceptual neighbors” of already available solutions or frameworks, and may be at least temporarily stuck on a local peak in the epistemic landscape. In fact, they may have simply been able to come up only with a bad lot of alternatives, and picking the best of a bad lot doesn’t really constitute knowledge, nor necessarily even mild progress.

The third account of scientific progress proposed to date is the semantic one presented by Niiniluoto (1980, 2011) and criticized by Bird (2007). Bird, somewhat grudgingly, given his propensity for epistemic theories of scientific progress, admits that semantic approaches are popular even among scientific realists (as opposed to functional accounts, usually endorsed by scientific anti-realists) because they — like the anti-realists — admit the force of the so-called pessimistic meta-induction in the history of science (Papineau 2010; Worrall 2012). This is the idea that, historically speaking, scientific theories have eventually been found to be wrong and have been replaced by new theories. [16] While the functionalist takes this as evidence that one simply cannot articulate a meaningful sense of progress in science, the semantic theorist responds that this is because — while scientific theories cannot (probably ever) be said to be “true” — they can be further from or closer to the truth.

The standard example is the transition in physics from Newtonian mechanics to Einstein’s general relativity. We know that Newtonian mechanics is wrong, in the sense of not providing an accurate account of fundamental aspects of the physical world, as it ought to if it were true. We also already know that Einstein’s theory is at the very least incomplete, and in that sense therefore it is also arguably “wrong,” since it does not mesh well with that other major theory in fundamental physics, quantum mechanics (the partial incongruence between the two is, of course, what has motivated the quest for a so-called “theory of everything,” for which string theories are potential candidates: Bailin and Love 2010; but see Smolin 2007). And yet, contra the functionalist, most scientists would want to claim that there is a sense in which Einstein’s theory is better than Newton’s, and specifically closer to the truth. How do we do that, given the problems with epistemic accounts of scientific progress based on the justified true belief concept of knowledge? One option is to turn to the semantic approach, and particularly to its core concept of “verisimilitude,” or truth-likeness: general relativity is closer to the truth in the sense of having a higher degree of verisimilitude with respect to its rival. This, of course, in turn raises the question of how to cash out the idea of verisimilitude itself.

Niiniluoto (1987), for example, developed a formal (and significantly technical) notion of truth-likeness: “closeness to the truth is explicated ‘locally’ by means of the distances of partial answers g in D(B) to the target h* in a cognitive problem B.” The first notion to unpack here is the one referring to local explication. The author rightly assumes that even if we are realists about the world (i.e., we are comfortable with the notion that there actually is a world out there with certain objective features, regardless of how much of those features can be discovered by human efforts), it will still be the case that the only way to attempt to understand such world is by deploying one or another properly suitable conceptual framework (“paradigm,” if one wishes to use Kuhn’s terminology). But, and here is the crucial point, there very likely isn’t going to be a single ideal framework capable of accounting for all phenomena in the world. This is why we have different “special” sciences (Fodor 1974), each with a certain domain of interest, tools, theories, methods, etc. That being the case, then it follows that verisimilitude is bound to be a local measure, because “more true” is quantifiable only within a given framework (or paradigm — Kuhn would have approved). This also immediately makes sense of the reference to a specific “cognitive problem” in Niiniluoto’s definition of verisimilitude given above: we are not talking about Truth in a cosmic sense, here; we are, rather, talking about the truth- likeness of notions concerning a specific and circumscribed problem, where again truth- likeness is measured relatively to currently available frameworks. [17] Niiniluoto’s approach is also sensitive to the sort of historical perspective that Kuhn first brought to the forefront of philosophy of science, and without which one simply cannot seriously engage in discussions of progress of science: “rational appraisal of theories is ... historical-bound to the best conceptual systems that we so far have been able to find” (1980, 445).

A standard response from functionalists like Laudan is going to be that it is not possible to articulate a meaningful sense of “closer to the truth” unless one has an independent way of estimating where such truth lies (this is, you will recall, the same sort of objection often raised against the correspondence theory of truth: what metric allows us to measure the degree of correspondence between our theories of the world and the, by definition unknown, state of the world itself?). But it is a utopian dream to somehow be able to obtain such an independent estimate, so where does that leave the semantic approach?

Niiniluoto’s answer is that the goal is not utopian at all, and is in fact analogous to what social and natural scientists do all the time when faced with estimating the value of variables that are not directly observable (such as “fitness” in biology, or “intelligence” in the social sciences). Indeed, a family of well understood and highly functional statistical methods have been designed precisely for this purpose, methods often referred to as structural equation modeling (Kline 2011). The approach consists in constructing one or more models of the phenomenon that one wishes to analyze, in terms of sets of linear equations relating dependent and independent variables that have been measured directly. The user, however, also has the option of specifying one or more hidden (“latent”) variable, i.e., variables that are postulated to play a causal role, yet could not be measured directly. This works as long as such variables are explicitly related, in the model, to others that can be subjected to measurement and that can reasonably be used as proxies for the hidden one. As Niiniluoto concludes: “There are evidential situations e and hypotheses h such that ver(h/e) is high. In such cases, it is rational for us to claim that the unknown degree of truthlikeness ... is also high, but this estimate may of course be wrong (and corrigible by further evidence)” (where ver=verisimilitude, 1980, 447).

I do not wish (and in fact I am not in a position, really) to adjudicate the ongoing debate among functionalists, epistemicists and semanticists about the nature (or existence) of scientific progress. Besides, there are several other important takes on the question of progress in science that have been proposed by philosophers over the past several decades and that I can do little more than mention in passing here, referring the interested reader to the proper technical literature. For instance, Philip Kitcher’s multidimensional account (Kitcher 1993; see update and discussion in Kaiser and Seide 2013), which stems from the author’s pragmatic naturalistic response to historiographers like Kuhn. For Kitcher scientific progress is indeed cumulative, but not in the straightforward manner proposed by Carnap and the logical positivists, since science proceeds along a number of dimensions, including the determination of natural kinds, the development of explanations, and an increasing approximation to truth (Kitcher 2012).

Another family of views on the progress of science as been termed “convergent realism,” and has been elaborated most prominently by Boyd (1973), but also Putnam (1978), and criticized by historicists and anti-realists like Laudan (1981b; see also Boyd 2007). This is the idea that scientific theories tend to be at least approximately true, with more recent theories getting closer to the truth, and that mature theories in an important sense preserve the theoretical (especially mathematical) relations of previous theories. We will examine this sort of reasoning further in a little bit, when I’ll discuss the debate between realists and antirealists in philosophy of science.

Or, finally, take Ian Hacking’s views as expressed in his Representing and Intervening (1983), which was also written in the context of that same realism-antirealism debate. Hacking’s “representing” is concerned with the variety of available accounts of scientific objectivity, but it is his “intervening” that is relevant here: in that part of the book he presents an in-depth discussion of experimental science, accompanied by a number of well developed examples (e.g., the use of microscopes in cell biology). He ends up admitting that if we limit our discussion to theoretical science, it is difficult to defend a realist position about scientific theories, which means that it is more difficult to articulate in what sense science makes progress (as opposed to being simply empirically adequate, as antirealists would maintain). But once we move to experiments, with the ability they afford us to control and manipulate systems and outcomes, it is much easier to defend the proposition that science makes actual teleonomic progress toward truth about the natural world.

What I hope the foregoing discussion has made clear is that — contra rather facile scoffing on the part of a number of publicly prominent scientists — philosophy actually has quite a bit to say about the nature of the scientific enterprise, highlighting the simple fact that even the seemingly uncontroversial idea that science makes progress is anything but. Before leaving this topic, however, we need to take a look at even more radical — and likely unpalatable to a number of scientists — philosophical ideas about the nature of science and scientific progress.

Progress in science: different philosophical accounts

The above discussion has largely been framed in terms that do not explicitly challenge the way most scientists think of their own enterprise: as a teleonomic one, whose ultimate goal is to arrive at (or approximate as far as possible) an ultimate, all-encompassing theory of how nature works, Steven Weinberg’s famous “theory of everything.” However, the epistemic, semantic and functionalist accounts do not all seat equally comfortably with that way of thinking. Bird’s epistemic approach can perhaps be most easily squared with the idea of teleonomic progress, since it argues that science is essentially about accumulation of knowledge about the world. The obvious problem with this, however, is that accumulation of truths is certainly necessary but also clearly insufficient to provide a robust sense of progress, since there are countless trivial ways of accumulating factual truths that no one in his right mind would count as scientific advances (e.g., I could spend a significant amount of grant funds to count exactly how many cells there are in my body, then in the body’s of the next person, and so on. This would hardly lead to any breakthrough in human cell biology, though.)

Niiniluoto’s semantic approach, based as it is on the idea of verisimilitude, is a little less friendly to the idea of a single ultimate goal for science. We have seen above that Niiniluoto’s way of cashing out “verisimilitude” is locally defined, and provides no way to compare how close we are to the truth on one specific problem, or even in a relatively broad domain, of science to another such problem or domain. So, for instance, progress toward truth about, say, ascertaining the neuronal underpinnings of human consciousness has prima facie nothing at all to do with progress in understanding how general relativity and quantum mechanics can be reconciled with each other in cases in which they give divergent answers.

Finally, the functionalist approach that can be traced to Kuhn and has been brought forth by Laudan, among several others, is even less friendly to a broad scale teleonomic view of science. Just recall Kuhn’s own skepticism about the possibility of a “coherent direction of ontological development” of scientific theories and his qualified distancing himself from a “relativist” view of scientific knowledge. If science is primarily about problem-solving, as both Kuhn and Laudan maintain, then there is only a limited sense in which the enterprise makes progress, Kuhn’s “evolutionary” metaphor notwithstanding.

But things can get even more messy for defenders of a straightforward concept of scientific progress — as, again, I take most scientists to be. As a scientist myself, I have always assumed that there is one thing, one type of activity, we call science. More importantly, though I am a biologist, I automatically accepted the physicists’ idea that — in principle at the least — everything boils down to physics, that it makes perfect sense to go after the above mentioned “theory of everything.” Then I read John Dupré’s The Disorder of Things (Dupré 1993), and that got me to pause and think hard.

I found Dupré’s book compelling not just because of his refreshing, and admittedly consciously iconoclastic tone, but also because a great deal of it is devoted to subject matters, like population genetics, that I actually know a lot about, and am therefore in a good position to judge whether the philosopher got it right (mostly, he did). Dupré’s strategy is to attack the idea of reductionism by showing how it doesn’t work in biology. He rejects the notion of a unified scientific method (a position that is nowadays pretty standard among philosophers of science), and goes on to advocate a pluralistic view of the sciences, which he claims reflects both what the sciences themselves are finding about the world (with a multiplication of increasingly disconnected disciplines and the production of new explanatory principles that are stubbornly irreducible to each other), as well as a more sensible metaphysics (there aren’t any “joints” at which the sciences “cut nature” — Kitcher’s “natural kinds” from above — so that there are a number of perfectly equivalent ways of thinking about the universe and its furnishings).

Dupré’s ideas have a long pedigree in philosophy of science, and arguably arch back to a classic and highly influential paper by Jerry Fodor (1974), “Special sciences (or: the disunity of science as a working hypothesis),” and are connected to Nancy Cartwright’s (1983) How the Laws of Physics Lie and Ian Hacking’s (1983) already mentioned Representing and Intervening.

Let me start with Fodor, whose target was, essentially, the logical positivist idea that the natural sciences form a hierarchy of fields and theories that are (potentially) reducible to each next level, forming a chain of reduction that ends up with fundamental physics at the bottom. So, for instance, sociology should be reducible to psychology, which in turn collapses into biology, the latter into chemistry, and then we are almost there. But what does “reducing” mean, in this context? At the least two things: call them ontological and theoretical. Ontologically speaking, most people would agree that all things in the universe are indeed made of the same substance, be it quarks, strings, branes or whatever; moreover, complex things are made of simpler things. For instance, populations of organisms are collections of individuals, while atoms are groups of particles, etc. Fodor does not object to this sort of reductionism. Theoretical reduction, however, is a different beast altogether, because scientific theories are not “out there in the world,” so to speak, they are creations of the human mind. This means that theoretical reduction, contra popular assumption among a number of scientists (especially physicists), does most definitely not logically follow from ontological reduction. Theoretical reduction was the holy (never achieved) grail of logical positivism: it is the ability to reduce all scientific laws to lower level ones, eventually reaching our by now infamous “theory of everything,” formulated of course in the language of physics. Fodor thinks that this will not do. Consider a superficially easy case. Typically, when one questions theory reduction in science one is faced with both incredulous stares and a quick counter-example: just look at chemistry. It has successfully been reduced to physics, so much so that these days there basically is no meaningful distinction between chemistry and physics. But it turns out after closer scrutiny that there are two problems with this move: first, the example itself is questionable; second, even if true, it is arguably more an exception than the rule.

As Weisberg et al. (2011) write: “Many philosophers assume that chemistry has already been reduced to physics. In the past, this assumption was so pervasive that it was common to read about ‘physico/chemical’ laws and explanations, as if the reduction of chemistry to physics was complete. Although most philosophers of chemistry would accept that there is no conflict between the sciences of chemistry and physics, most philosophers of chemistry think that a stronger conception of unity is mistaken. Most believe that chemistry has not been reduced to physics nor is it likely to be.” For instance, both Bogaard (1978) and Scerri (1991, 1994) have raised doubts about the feasibility of reducing chemical accounts of molecules and atoms to quantum mechanics. Weisberg et al. (2011) add examples of difficult reductions of macroscopic to microscopic theories within chemistry itself (let alone between chemistry and physics), even in what are at first glance obviously easy cases, like the concept of temperature. I will refer the reader to the literature cited by Weisberg et al. for the fascinating arguments that give force to this sort of cases, but for my purposes here it suffices to note that the alleged reduction has been questioned by “most” philosophers of chemistry, which ought to cast at least some doubt on even this oft- trumpeted example of theoretical reduction. Another instance, closer to my own academic home field, is Mendelian genetics, which has also not been reduced to molecular genetics, contra to what commonly assumed by a number of geneticists and molecular biologists (Waters 2007). In this case one of the problems is that there are a number of non-isomorphic concepts of “gene” being used in biology, which gets in the way of achieving full inter-theoretical reduction.

Once we begin to think along these lines, the problems for the unity of science thesis — and hence for straightforward accounts of what it means to have scientific progress — are even worse. Here is how Fodor puts it, right at the beginning of his ’74 paper: “A typical thesis of positivistic philosophy of science is that all true theories in the special sciences [i.e., everything but fundamental physics, including non-fundamental physics] should reduce to physical theories in the long run. This is intended to be an empirical thesis, and part of the evidence which supports it is provided by such scientific successes as the molecular theory of heat and the physical explanation of the chemical bond. But the philosophical popularity of the reductivist program cannot be explained by reference to these achievements alone. The development of science has witnessed the proliferation of specialized disciplines at least as often as it has witnessed their reduction to physics, so the wide spread enthusiasm for reduction can hardly be a mere induction over its past successes.” In other words, echoing both Fodor and Dupré one could argue that the history of science has produced many more divergences at the theoretical level — via the proliferation of new theories within individual “special” sciences — than it has produced successful cases of reduction. If anything, historical induction points the other way around from the commonly accepted story.

Turns out that even some scientists seem inclined toward at least some bit of skepticism concerning the notion that “fundamental” physics is so, well, (theoretically) fundamental. (It is, again, in the ontological sense discussed above: everything is made of quarks, or strings, or branes, or whatever.) During the 1990’s the American scientific community witnessed a very public debate concerning the construction of a Superconducting Super Collider (SSC), which was the proposed antecedent of the Large Hadron Collider that recently led to the discovery of the Higgs boson. The project was eventually nixed by the US Congress because it was too expensive. Steven Weinberg testified in front of Congress on behalf of the project, but what is less known is that some physicists testified against the SSC, and that their argument was based on the increasing irrelevance of fundamental physics to the rest of physics — let alone to biology or the social sciences. Here is how solid state physicist Philip W. Anderson (1972) put it early on, foreshadowing the arguments he later used against Weinberg at the time of the SSC hearings: “The more the elementary particle physicists tell us about the nature of the fundamental laws, the less relevance they seem to have to the very real problems of the rest of science.” So much for a fundamental theory of everything.

Let us go back to Fodor and why he is skeptical of theory reduction, again from his ’74 paper: “If it turns out that the functional decomposition of the nervous system corresponds to its neurological (anatomical, biochemical, physical) decomposition, then there are only epistemological reasons for studying the former instead of the latter [meaning that psychology couldn’t be done by way of physics only for practical reasons, it would be too unwieldy]. But suppose there is no such correspondence? Suppose the functional organization of the nervous system cross cuts its neurological organization (so that quite different neurological structures can subserve identical psychological functions across times or across organisms). Then the existence of psychology depends not on the fact that neurons are so sadly small, but rather on the fact that neurology does not posit the natural kinds that psychology requires.” And just before this passage in the same paper, Fodor argues a related, even more interesting point: “If only physical particles weren’t so small (if only brains were on the outside, where one can get a look at them), then we would do physics instead of paleontology (neurology instead of psychology; psychology instead of economics; and so on down). [But] even if brains were out where they can be looked at, as things now stand, we wouldn’t know what to look for: we lack the appropriate theoretical apparatus for the psychological taxonomy of neurological events.”

The idea, I take it, is that when physicists say that “in principle” all knowledge of the world is reducible to physics, one is perfectly within one’s rights to ask what principle, exactly, are they referring to. Fodor contends that if one were to call up the epistemic bluff the physicists would have no idea of where to even begin to provide a reduction of sociology, economics, psychology, biology, etc. to fundamental physics. There is, it seems, no known “principle” that would guide anyone in pursuing such a quest — a far more fundamental issue than the one imposed by merely practical limits of time and calculation. To provide an analogy, if I told you that I could, given the proper amount of time and energy, list all the digits of the largest known prime number, but then decline to actually do so because, you know, the darn thing’s got 12,978,189 digits, you couldn’t have any principled objection to my statement. But if instead I told you that I can prove to you that there is an infinity of prime numbers, you would be perfectly within your rights to ask me at the least the outline of such proof (which exists, by the way), and you should certainly not be content with any vague gesturing on my part to the effect that I don’t see any reason “in principle” why there should be a limit to the set of prime numbers.

Tantalizing as the above is for a philosopher of science like myself, in order to bring us back to our discussion of progress in science we need some positive reasons to take seriously the notion of the impossibility of ultimate theory reduction, and therefore to contemplate the idea of a fundamental disunity of science and what it may mean for the idea of progress within the scientific enterprise. Cartwright (1983) and Hacking (1983) do put forth some such reasons, even though of course there have been plenty of critics of their positions. Cartwright has articulated a view known as theory anti-realism, which implies a denial of the standard idea — almost universal among scientists, and somewhat popular among philosophers — that laws of nature are (approximately) true generalized descriptions of the behavior of things, especially particles (or fields, doesn’t matter). Rather, Cartwright suggests that theories are statements about how things (or particles, or fields) would behave according to idealized models of reality.

The implication here is that our models of reality are not true, and therefore that — strictly speaking — laws of nature are false. The idea of laws of nature (especially with their initially literal implication of the existence of a law giver) has been controversial since it was championed by Descartes and opposed by Hobbes and Galileo [18], but Cartwright’s suggestion is rather radical. She distinguishes between two ways of thinking about laws: “fundamental” laws are those postulated by the realists, and they are meant to describe the true, deep structure of the universe. “Phenomenological” laws, by contrast, are useful for making empirical predictions, they work well enough for that purpose, but strictly speaking they are false.

Now, there are a number of instances in which even physicists would agree with Cartwright. Take the laws of Newtonian mechanics: they do work well enough for empirical predictions (within a certain domain of application), but we know that they are false if they are understood as being truly universal (precisely because they have a limited domain of application). According to Cartwright, however, all laws and scientific generalizations, in physics as well as in the “special” sciences are just like that, phenomenological. [19] And there are plenty of other examples: nobody, at the moment, seems to have any clue about how to even begin to reduce the theory of natural selection, or economic theories, for instance, to anything below the levels of biology and economics respectively, let alone fundamental physics. If Cartwright is correct (and Hacking argues along similar lines), then science is fundamentally disunified, and its very goal should shift from seeking a theory of everything to putting together the best patchwork of local, phenomenological theories and laws, each one of which, of course, would be characterized by its proper domain of application.

Here is how Cartwright herself puts it, concerning physics in particular: “Neither quantum nor classical theories are sufficient on their own for providing accurate descriptions of the phenomena in their domain. Some situations require quantum descriptions, some classical and some a mix of both.” And the same goes, a fortiori, for the full ensemble of scientific theories, including all those coming out of the special sciences. So, are Dupré, Fodor, Hacking and Cartwright, among others, right? I don’t know, but it behooves anyone who is seriously interested in the nature of science to take their ideas seriously. If one does that, then it becomes far less clear that “science” makes progress, although one can still articulate a very clear sense in which individual sciences do.

The goal of this chapter was to show that the concept of progress in science — which most scientists and the lay public seem to think is uncontroversial and self-evident — is anything but. This does not mean at all that we do not have good reasons to think that science does, in fact, make progress. But when scientists in particular loudly complain that philosophy doesn’t progress they should be reminded that it is surprisingly difficult to articulate a coherent and convincing theory of progress in any discipline, including their own — where by their account it ought to be a no brainer. In the next chapter we will pursue our understanding of progress in different fields of inquiry by turning to mathematics and logic, were I think the concept definitely applies, but in a fashion that is interestingly distinct from the sense(s) in which it does in science. And it will be from a better understanding of progress in both science(s) and mathematics-logic that we will eventually be in a position to articulate how philosophy (or at least certain fields within philosophy) are also progressive.

5. Progress in Math and Logic

“Contrariwise, continued Tweedledee, if it was so, it might be; and if it were so, it would be; but as it isn’t, it ain’t. That’s logic.”
(Lewis Carroll)

Despite all the complications we have examined in the previous chapter — historical as well as epistemological — involved in the deceitfully simple task of making sense of the idea of progress in science, I think it is undeniable that science does, in fact, make progress, and indeed constitutes one of the clearest examples of a discipline (or, rather, a set of disciplines) that does so. Here I turn to the closely connected fields of mathematics and logic, for a number of reasons.

First, mathematics in particular is often thought of as not only having made clear progress throughout its history, but as having done so in an even less equivocal sense than that of science. After all — at first sight at least — scientific theories are often overturned (think of the replacement of Newtonian mechanics by Einstein’s relativity), while a mathematical theorem, once proven, stays firmly put into the set of things we (think we) know for sure. Second, the history of logic is more uneven, with clear hallmarks of progress, but also extremely long periods of stasis, and therefore presents us with a dynamics of “progress” that is definitely distinct from that of science as well as sufficiently different from the one that applies to mathematics to provide an additional useful contrast class. Third, I think the comparison among these three areas of human endeavor (science, mathematics, and logic) will help us pinpoint more exactly in what sense philosophy itself makes progress, as the latter discipline shares aspects of the other three without really being the same animal as any of them.

As a preliminary, however, it will help to briefly discuss the general relationship between mathematics and logic, as seen by practitioners in these fields, something I have become fascinated with ever since reading my first book on the philosophy of mathematics (Brown 2008). According to Cameron (2010) [20] there are two roles that logic plays in mathematics. The first deals with providing the foundations on which the mathematical enterprise is built. As he puts it: “No mathematician ever writes out a long complicated argument by going back to the notation and formalism of logic; but every mathematician must have the confidence that she could do so if it were demanded.” The second role is played by logic as a branch of mathematics, on the same level as, say, number theory. Here, according to Cameron, logic “develops by using the common culture of mathematics, and makes its own rather important contributions to this culture.” For him, therefore, the relationship between logic and mathematics is not along the lines of one being a branch of the other, exactly. Rather, certain logical systems can be deployed inside mathematics, while others are in an interesting sense outside of it, meaning that they provide (logical) justification for mathematics itself.

Berry (2010) approaches the issue of the relationship between logic and mathematics in a more comprehensive and systematic manner. She puts forth that the answer to the question depends (not surprisingly, perhaps) on what exactly one means by “logic.” In particular, she provides a useful classification of five meanings one might have in mind when using the word:

First order logic.
Fully general principles of good reasoning.
A collection of fully general principles which a person could learn and apply.
Principles of good reasoning that are not ontologically committal.
Principles of good reasoning that no sane person could doubt. [21]

Berry’s first point is that we know that it is not possible to program a computer to produce all and only the truths of number theory, but it is possible to program such computer to produce all the truths of first order logic. Which means that mathematics is not the same as logic if one understands the latter to be the first order stuff (option #1 above). Berry adds that if we make the further assumption that human reasoning can be modeled in a computer program, then logic doesn’t capture all of mathematics also in cases #3 and #5 above. What about #2, then? To quote Berry: “If by ‘logic’ you just mean ... fully general principles of reasoning that would be generally valid (whether or not one could pack all of these principles into some finite human brain) — then we have no reason to think that math isn’t logic.” I am very sympathetic to this broader reading of logic, but we are still left with option #4. Apropos of that Berry reminds her readers that standard mathematics is reducible to set theory, and that the latter in turn has been shown to be reducible to second-order logic, thus implying that mathematics is, after all, a branch of logic.

Berry’s conclusion is that “it is fully possible to say ... that math is the study of ‘logic’ in the sense of generally valid patterns of reasoning. However, if you say this, you must then admit that ‘logic’ is not finitely axiomatizable [because of Gödel’s theorems: Raatikainen 2015], and there are logical truths which are not provable from the obvious via obvious steps (indeed, plausibly ones which we can never know about). ... What Incompleteness shows [then] is that not all logical truths can be gotten from the ones that we know about.”

This contrast between Berry’s and Cameron’s analyses helps me make the point that mathematics and logic are indeed deeply related, which further justifies treating them in a single chapter in this book, even though the exact nature of that relationship is still very much up for discussion among practitioners of these fields. My objective here, of course, regardless of whether you think mathematics is a branch of logic or vice versa (or, perhaps, that both disciplines are instantiations of a broader way of reasoning about abstract objects — as I am inclined to believe), is to show that both have clearly made progress over the past two millennia or more — albeit in an interestingly different fashion from each other and from science. Let us begin with mathematics first.

Progress in mathematics: some historical considerations

Somewhat surprisingly, mathematicians may experience a similar problem to that encountered by philosophers in precisely defining what it is that they do. Weil (1978) paraphrases Houseman on poetry, saying that “[the mathematician] may not be able to define what is a mathematical idea, but he likes to think that when he smells one he knows it.” He goes on to acknowledge the existence of transitional stages between folk ideas about the world and distinctly mathematical ones: the concept of a icosahedron, for instance, is definitely an example of a mathematical idea, while more mundane geometrical figures, like circles, rectangles and cubes are clearly part of the thinking tools of laypeople. Philosophers also often incorporate “folk concepts” (say, free will) in their parlance, but end up having a tougher time than either mathematicians or scientists in convincing outsiders that there is more technical content to what they do than it may appear from a cursory examination of their debates. While it is hard to imagine a non- mathematician commenting seriously on technical issues in geometry just because he knows what a square is, it seems like everyone feels free to blunder into discussions of metaphysics because they think they know what the pros are talking about (or, worse, that they certifiably know better than said pros).

In this section, and pretty much in the remainder of the chapter, I will take an historical approach to the subject matter under discussion, as I think it is by far the most informative and easy to follow. However, I need to acknowledge that there are a number of ways of conceiving of progress in mathematics that I will not entertain, or that I will mention only in passing. It is my belief that even if I did incorporate them (into what would then become a much longer, and significantly more unwieldy, chapter) they would not alter my main conclusion: that mathematics does make progress, and that it does so in ways that are significantly different from how science proceeds.

To begin with, then, there is the thorny issue of mathematical Platonism, which I have tackled in part in the Introduction. Platonism, which comes in a variety of flavors (Balaguer 1998; Linnebo 2011), is a popular position among both mathematicians and philosophers of mathematics — though of course there are many who reject it, resulting into a large and fascinating literature. If one is a Platonist in mathematics, then one may deploy the mathematical equivalent of a correspondence theory of truth, which we have seen is the one assumed by most scientists (Chapter 4). As a result one might think that it is legitimate to conclude that mathematics makes progress in a very similar way to how science does.

There are two issues that arise in connection with this and are germane to my project. First, all the non trivial problems associated with the deployment of a correspondence theory of truth that we have seen in the previous chapter would still hold for its deployment with respect to the field of mathematics. Second, and more importantly, the sense of “correspondence” here must be different, since Platonic forms are neither to be found “out there” nor are they accessible by empirical means of any sort (indeed, one of the most powerful objections to Platonism is the lack of a reasonable account of how, precisely, mathematicians do gain access to the alleged Platonic realm). These are not insuperable problems, but I maintain that in order to deal with them one has to shift to talk of progress in conceptual (as opposed to empirical) space in mathematics, the very same talk that I think holds also in the cases of logic and philosophy. This in turn means that mathematics cannot be conceived in the same teleonomic fashion that most views of science allow, which means that my main argument here will stand. In fact, I am tempted to say that mathematics and logic, very much unlike what is usually argued for science, not only are not aiming at any “final theory,” but in fact generate their problems internally and expand their concerns in an autonomous fashion throughout the course of their history, without aiming at any unified goal. In that sense, they work perhaps in a way similar — though not identical — to how the sciences can be understood to work if one buys into a more radical notion of the disunity of science itself, similar to those presented by Fodor, Cartwright, Hacking and Dupré and discussed at the end of the last chapter.

A related worry may arise if a theorist sees mathematics as a set of formal systems that are interpretable in ways that aid natural scientific inquiry, similar to the Quineian “naturalistic” view that we have discussed in Chapter 3. From that standpoint, progress in mathematics would then consist in adding formal systems that can be deployed in new scientific ventures. I submit, however, that this would amount to a very impoverished view of mathematics, essentially relegating the enterprise to a subordinate role as handmaiden to science. I think there are obvious reasons to reject such a role in both the cases of mathematics and logic, reasons that are rooted in the historical record and the actual contemporary practices of mathematicians and logicians: many problems in both fields are internally generated, and are neither derived, nor do they get their validation, from science. This, of course, does not deny the obvious fact that both mathematics and logic are — more than occasionally — extremely useful to scientific practice.

Yet another conceivable view would be to sidestep the issue of mathematical truth altogether and approach mathematical progress directly in terms of the deepening of our mathematical understanding. Standard examples of progress in mathematics would then make sense accordingly: for example, Descartes’ development of analytic geometry enabled us to find a general method of solving locus problems; the tradition that runs from Lagrange to Galois successively deepens our understanding of methods for solving polynomial equations of different degrees; Dedekind’s construction of the real numbers enables us to understand the principles of real analysis [22], and so on. Mathematical progress, following this view, is a type of explanatory progress, a thesis that is ontologically neutral and needs not take sides on the issue of Platonism. This view of (internally generated) progress as deepening of our understanding of a given domain of knowledge can be extended to logic (and, in part, to philosophy), and is — I think — perfectly compatible with the thesis that I develop in this book.

The above qualifications having been made, there likely is no more obvious place to start for a brief historical overview of progress than by arching back to the ancient Greeks (Bergrren 1984). Broadly speaking, the Greeks deployed three approaches to mathematics: the axiomatic method, the method of analysis, and geometric algebra — all of which embodied a more sophisticated modus operandi than that typical of Babylonian mathematics, by which the Greeks were clearly inspired.

The standard example of axiomatic method is Euclidean arithmetics (Szabó 1968), exemplified for instance by the theory of proportions. I am interested here in the connections that this approach had with philosophy, particularly the Eleatic school to which Zeno (he of the famous paradoxes) belonged, as well as disciplines that today we consider more remotely connected to either mathematics or philosophy. For instance, one of the problems that was initially addressed by means of Euclidean arithmetics had to do with musical theory, and in particular the issue of how to divide the octave into two equal intervals. This, in turn, fed back into theoretical mathematics, since it generated an interest in incommensurable quantities. The second approach, geometric analysis (Mahoney 1968), led to both a preoccupation with general problems in geometry and to the solution of specific issues, such as trisecting the angle. Again, there was a tight connection with philosophy at the time, since geometric analysis — while not actually invented by Plato, as it has sometimes been suggested — certainly inspired him to elaborate his ideas on dialectic philosophy. The third approach used by the Greeks to address mathematical- philosophical problems was geometric algebra, classically embodied by one of the most influential books ever written in the history of mathematics, Euclid’s Elements. Geometric algebra is interpreted by historians of mathematics as a translation of the Babylonian approach to algebra into geometric language, and thus provides us with an example of progress insofar such “translation” allowed the Greeks to address a much wider range of problems than the Babylonians had been capable of (or interested in).

What did the ancient Greeks accomplish with this array of new tools at their disposal? Quite a bit, as it turns out. The list is long and well known to anyone familiar with the basics of mathematics, but it is worth remembering that it includes the foundations of a whole class of geometry (Euclid), the theory of proportions (Pythagoras, Eudoxos), and the theory of incommensurables (early Pythagoreans, Theodoros, Theaetetos), to mention but a few. Archimedes’ work alone was of crucial importance. Setting aside his output on the theory of levers, Bashmakova (1956) has suggested that Archimedes’ had developed a method for finding extrema (i.e., the maximum or minimum, local or global, of a given function) that was rediscovered only in the 16th and 17th centuries by Ricci and Torricelli. And then there is Ptolemy, whose work was pivotal for the history of mathematical methodology and of trigonometry, and likely instrumental for the origin of the very idea of mathematical function. In fact, Greek geometry provided the foundations for a more modern treatment of continuous phenomena in general, a marked advance over the Babylonian focus on discrete quantities.

Beyond the Greeks the history of mathematics gets much more complex, and I will comment on a few more examples of what I think is obvious progress below. However, it is interesting to note what mathematicians and historians of mathematics say about the dynamics of the field. For instance, take the classic comments by André Weil (1978) on the unfolding of history of mathematics. He begins by highlighting the convergence of mathematical discoveries across time and cultures, as in the case of the discovery of certain classes of power series expansions, which took place independently in Europe, India and Japan. Or the solution to Pell’s equation, achieved first in India in the 12th century, then again in Europe — following work by Fermat — in 1657.

Weil echoes Leibnitz’s approach to getting acquainted with the nature of mathematical practice. Leibnitz thought that we should look at “illustrious examples” to learn about what he called “the art of discovery.” Doing that, according to Weil, clearly shows that mathematicians often directly concern themselves with long-range objectives, as opposed to the “puzzle solving” (to use Kuhn’s phrase) of much empirical science, which in turn means that practitioners benefit from an awareness of broad trends and the evolution of mathematical ideas over long periods of time. The reason I find this interesting is because it is not very different from the way philosophers regard the history of ideas in their own field, and very much in contrast to the general neglect of the history of science that scientists often display. Underlying this contrast may be that philosophy and mathematics (and, we shall soon see, logic) make progress across relatively long time spans, while scientific discovery is often fast paced by comparison, so that history rapidly becomes less relevant in the latter case.

When considering the history of ideas (and therefore the progress made) in mathematics, science, and philosophy, an important issue that is often overlooked is the distinction between history proper and what Grattan-Guiness (2004) labelled “heritage.” History, in this context, refers to the development of a given idea or result, while heritage refers to the impact that idea or result had on further work, when seen from a modern vantage point. Approaching things from a heritage perspective tends to focus on the results obtained, while a properly historical approach takes a comprehensive look also at the causes and motivations of certain developments. It should be obvious that it is important to keep the two separate, on penalty of incurring in anachronistic readings of the history of any given field, a recurring problem especially in the sciences, where practitioners learn a highly sanitized (one would almost want to say romanticized), introductory textbook version of the history of science.

A well documented example of the difference, discussed by Grattan-Guiness, is that of Book 2, Proposition 4 in the already mentioned Elements by Euclid, which concerns a theorem for the completion of a square, nowadays a method to solve quadratic equations. Beginning in the late 19th century there has been a tendency to interpret this as evidence that Euclid was a geometric algebraist, i.e., essentially focused on algebra. But historians of mathematics have pointed out that a more sound (and not anachronistic) reading of the actual history shows Euclid’s theorem to be firmly within the bounds of geometry. The point is that, although historians have set the record straight, a number of mathematicians still cling to the earlier interpretation, presumably because they are interested in the knowledge content, not the actual development, of Euclid’s ideas — thus confusing history and heritage.

Another example is provided by Lagrange’s work in the 18th century. He understood that there was a connection between the algebraic solvability of polynomial equations and the properties of some functions of the roots of those polynomials. Lagrange’s ideas played a crucial role in the subsequent development of what is now known as group theory (i.e., a theory of a broad type of algebraic structures), but the original insight should not be described in terms of group theory, because that would confuse things and distort the sequence of historical developments. As Grattan-Guiness (2004, 171) aptly puts it: “The inheritor [his term for people who disregard the history of ideas] may read something by, say, Lagrange and exclaims: ‘My word, Lagrange here is very modern!’; but the historian should reply: ‘No, we are very Lagrangian.’” This should strike a chord with both scientists and especially philosophers, who are at times guilty of precisely the same kind of historical reading-by-hindsight. Grattan-Guiness (2004, 169, 171) summarizes the difference between heritage and history in this way: “Heritage is likely to focus only upon positive influence, whereas history needs to take note also of negative influences, especially of a general kind, such as reaction against some notion or the practice of it or importance accorded some context ... Heritage resembles Whig history, the seemingly inevitable success of the actual victors, with predecessors assessed primarily in terms of similarities with the dominant position.”

So, what do we learn from the actual history of mathematics, as opposed to a glorified consideration of its heritage? One of the fundamental notions that emerge is that the development of a number of mathematical theories has been slow, or even characterized by long periods of stasis. It is therefore an interesting exercise for the contemporary practicing mathematician to meditate on which current theories may be in a stage of arrested (but perhaps eventually to be resumed) development, since looking at mathematics from the standpoint of heritage may provide a false view of the field as inevitably progressing by accumulation of more refined theories, while the real story also includes a number of abandoned or faded away notions.

Following Grattan-Guiness, the history of mathematics — again like the history of science — has also demonstrably been affected by social and even political forces completely external to the field. For instance, in the 19th century French mathematicians worked largely on mathematical analysis, while their English colleagues focused on new algebras, just like, say, during the middle part of the 20th century Soviet geneticists (before the Lysenko disaster: Joravsky 1970) adopted a distinctly more developmental approach to the study of organisms than their Western European counterparts. The message is that it is worthwhile to escape from the all too easy trap of thinking that whatever question or approach is currently being pursued by one’s own intellectual community is the inherently best or most interesting one. These considerations also carry consequences in terms of education: mathematics — like much of science — even when taught with a historical perspective, is actually presented in heritage fashion, smoothing over the irregularities and the setbacks. Consequently, students get a misleading view of a series of finished products with no sense of why the questions were raised to begin with, or of what struggle ensued in the attempt to answer them. This in turn yields a false image of constant linear progress that artificially inflates the differences between disciplines that appear to make clear progress (mathematics, science) and those that appear more stagnant (philosophy, other parts of the humanities).

History of mathematics: the philosophical approach

It is interesting to note that mathematicians and historians of mathematics have often taken what can be characterized as a decidedly philosophical approach to the understanding of the development of their field. One example is provided by Mehrtens’ (1976) influential paper about the applicability of the (then relatively recently articulated) ideas by Kuhn to the field of mathematics.

Mehrtens begins by suggesting that mathematics can be thought of as being about “something” that offers resistance (without having to go so far as to invoke a special ontology of mathematical problems or objects — as in the case of mathematical Platonism: Maddy, 1990; Balaguer 1998; Bigelow 1998), and while the problems of mathematics are more markedly internally generated when compared to those of the natural sciences, he thinks the analogy holds in the sense that “the relation between mathematicians and their subject is very much like that of the natural sciences” (Mehrtens 1976, 300). Does this “resistance” yield Kuhn-like periods of revolution in mathematics? Crowe (1975) had denied that possibility (more on his paper below), but Mehrtens advances the example of the shift to differential notation catalyzed by the work of Robert Woodhouse at the beginning of the 19th century as a possible instance of Kuhnian revolution in mathematics. Nonetheless, even Mehrtens agrees that there are few (if any) examples of mathematical theories that have been overthrown, with gradual change or increasing obsolescence accounting for most instances of change instead.

Even though it is debatable whether there have been paradigm shifts in the Kuhnian sense in mathematics, there certainly have been Lakatos-type (1970) research programs. As we have seen in the previous chapter, Lakatos was attempting to improve on both Popper’s (1963) prescriptive and Kuhn’s (1963) descriptive approaches in philosophy of science, proposing that at any given moment there may be more than one active research program pursued by scientists (or mathematicians). Recall that these programs have a hard, non- negotiable theoretical core, figuratively surrounded by a soften “protective belt” made of ancillary hypotheses and methods that can be negotiated, revised or abandoned during the development of the program (while retaining the core). A successful research program, then, is progressive in the sense that it keeps generating fruitful scholarship. But research programs may stall and eventually degenerate when they fail to lead to further insights or applications. In mathematics, an instance of shifting from a potentially degenerating to a progressive research program may have occurred at the turn of the 20th century, when there was a change in emphasis away from applying mathematics to logic and toward using instead symbolic logic to explore foundational questions in mathematics itself.

Setting aside revolutions, though, the Kuhnian approach to historiography is rich of other concepts that may still apply, at least partially, to mathematics, and help us understand in what sense and how it makes progress. For instance, there have been episodes in the history of the field that do resemble Kuhn’s description of scientific crises, except that the resolution of such crises did not cause the kind of paradigm shift that Kuhn famously described as taking place in, for instance, physics. The reason for the difference is that mathematicians, when faced with a crisis, have focused on the fruitfulness and applicability of their theories, and they have benefited from the interactions between mathematics and other fields, all of which — as Lakatos (1963/64) pointed out, essentially diffuses a Kuhnian crisis.

What about another element of the Kuhnian view, the treatment of anomalies within a given field, the accumulation of which in physics eventually leads to the onset of a crisis and the occurrence of a paradigm shift? The history of mathematics certainly presents a number of cases of anomalies, such as Euclid’s Fifth Postulate [23]. The 5th was an anomaly from the beginning, because unlike Euclid’s other four postulates, it is not self- evident. Moreover, without it, Euclid could not prove his theorems, which is why people sought a proof of it for two millennia. It was the realization, by the 19th century, that the search was going to be fruitless that led people to explore what today we call non- Euclidean geometries, as well as to abandon the “metaphysical” belief in a single unifying geometry. This sort of historical pattern, Mehrtens suggests, is rather general in the history of mathematics.

Historical patterns notwithstanding, the emotional response of the mathematical community to an anomaly is a question for sociology and psychology of the discipline and its practitioners (just as in the case of science under analogous circumstances), but it has sometimes made an impact, as in the famous case of the extremely negative reaction of the Pythagoreans to the idea of incommensurability, i.e., the existence of irrational numbers like π. Incommensurability was apparently discovered by the Pythagorean Hippasus of Metapontum. When Pythagoras — who allegedly was out of town at the time — got back and understood what Hippasus had done he was so upset that he had his pupil thrown overboard and drowned!

There are two other similarities between the way things work in mathematics and Kuhn’s description of the scientific process (and progress): the idea of normal science and the characteristics of the scholarly community itself. As we have seen, for Kuhn the history of a field is characterized largely by long periods of “normal science,” in between the relatively brief instances of crisis and paradigm shifting. Mehrtens readily agrees that much of what is done in everyday mathematical scholarship similarly falls under “normal mathematics,” and that it is this process that eventually leads to the sort of textbook-type streamlined and elegant formulations of a given theorem. Kuhn also thought of science as being characterized by a relatively well defined community of practitioners who share the same values (epistemic as well as others, including aesthetic ones) and procedures (theoretical as much as empirical). Again, this is certainly the case also for modern mathematics, although when one goes further back in time in the history of either science or mathematics, what counts as the relevant “community” is far more murky.

One of Kuhn’s more mature concepts — which actually replaced the initial idea of a paradigm in his later writings — is that of a disciplinary matrix (Chapter 4). This, too, unquestionably applies to mathematics. Mathematicians share concepts, theories, methods, terminology, values, and aesthetic preferences, though the importance of different values changes over time. For instance, throughout the history of imaginary numbers fruitfulness dominated over rigor, but the latter gained more currency as a value throughout the 19th century. Also important to mathematics’ disciplinary matrix are so- called exemplars, which include Euclid’s Elements, Gauss’ Disquisitiones Arithmeticae, and other standard works that characterize the field, its methods and problems. Exemplars include procedures, such as the geometric representation of complex numbers. Mehrtens mentions a number of standard problems in mathematics that are part of the disciplinary matrix, such as factorization procedures. These have wide application to a variety of specific mathematical problems, and yet do not require the availability of complete solutions. In fact, a good number of the so-called “open problems” presented in textbooks fall within this category. Concepts also play a Kuhnian-style role, that of symbolic generalizations, within mathematics’ disciplinary matrix. Consider, for instance, the fundamental role of the concept of function: according to Mehrtens, if a mathematician doesn’t care much about ontology (i.e., she is not metaphysically inclined) then concepts pretty much determine what she thinks exists (or doesn’t exist) in the realm of mathematics. All of these components influence the very way in which mathematicians think about their subject matter, just like standard works (Newton’s Principia, Darwin’s Origin, and so forth) and exemplars (Galileo’s thought experiments, the study of natural selection in Galapagos finches) play an analogous role in the natural sciences.

What does all of this tell us about progress in mathematics? Mehrtens points out that sometimes changes in the disciplinary matrix occur despite the conscious efforts of the originators of the changes themselves. In astronomy, Kepler struggled mightily before giving up the (metaphysical) assumption that the orbits of the planets had to be circular. In mathematics, Hamilton invented quaternions [24] after trying hard for a long time not to abandon the principle of commutativity (the idea that in a given operation changing the order of the operands does not change the result) that was characteristic of the then current disciplinary matrix. So change sometimes occurs despite the resistance of some of the very practitioners who are later seen as the agents of that change. And, as is the case in science, mathematical discoveries often appear to be “in the air,” meaning that several mathematicians converge on a particular solution to a given problem, a phenomenon that is likely explained by the social bounds within the community made possible by the field’s disciplinary matrix.

There are of course other ways of reflecting on the nature of mathematics, in some aspects diverging from the one sketched out by Mehrtens. Without pretending to be either exhaustive or in a position to adjudicate disagreements among historians of mathematics, I will devote the rest of this section to two classic papers by Michael J. Crowe (1975, 1988), because I think they provide the non mathematician with useful and insightful views on how mathematics works, and especially — as far as my purposes here are concerned — in which respects it is similar to or different from the natural sciences [25].

Crowe (1975) presented what he thought are ten “laws” of mathematical history, in an attempt to differentiate the history of mathematics from that of the natural sciences on the basis of the diverging conceptual structures of the two fields. A rapid glance at Crowe’s list, however, shows a rather complex picture, with more similarities between mathematics and science than he perhaps realized or was willing to grant. For instance, he begins with “New mathematical concepts frequently come forth not at the bidding, but against the efforts, at times strenuous efforts, of the mathematicians who create them,” which is something that more than occasionally happens in science as well, for example in the just mentioned case of Kepler’s initial (and prolonged) refusal to move away from the assumption of circularity of planetary orbits, or of Einstein’s famous regret at the introduction of his cosmological constant, which turned out to be an inspired and fruitful move after all.

“Many new mathematical concepts, even though logically acceptable, meet forceful resistance after their appearance and achieve acceptance only after an extended period of time,” an example of which is the invectives deployed as a common response to the idea of square roots of negative numbers between the mid-16th century and the early 19th century. Then again, in science Alfred Wegener’s idea of continental drift and Lynn Margulis’ contention that several sub-cellular organelles originated by symbiosis between initially independent organisms were also greeted with scorn, just to mention a couple of instances from the history of science. Crowe continues: “Although the demands of logic, consistency, and rigor have at times urged the rejection of some concepts now accepted, the usefulness of these concepts has repeatedly forced mathematicians to accept and to tolerate them, even in the face of strong feelings of discomfort.” For instance, mathematicians accepted the idea of imaginary numbers for more than a century despite the lack of formal justification, because they turned out to be useful, both internally to mathematics and externally, as in the cases of applications to quantum physics, engineering, and computer science. Again, it’s not difficult to find analogous episodes in the history of science, though usually across significantly shorter time scales — as with the gradual acceptance, after a period of significant unease, of the idea of light quanta at the beginning of the 20th century (Baggott 2013).

“The rigor that permeates the textbook presentations of many areas of mathematics was frequently a late acquisition in the historical development of those areas and was frequently forced upon, rather than actively sought by, the pioneers in those fields.” We have encountered this above, during our discussion of the difference between the history of mathematics and the presentation of mathematical heritage. Again, examples are not difficult to find, and Crowe mentions increasing standards for the acceptability of proof, with those characteristics of mathematical practice before the 19th century having been superseded by new, more rigorous ones by the end of the 19th century, standards that in turn would not be acceptable in contemporary practice. Analogously, both observational and experimental standards have definitely been ratcheted up during the history of individual natural sciences, in part — obviously — as a result of technological improvement and the consequent amelioration of observational and experimental tools, but also because of theoretical-conceptual refinements, for instance the introduction of Bayesian thinking in disciplines as varied as medical and ecological research (Ogle 2009; Kadane 2011).

For Crowe “the ‘knowledge’ possessed by mathematicians concerning mathematics at any point in time is multilayered. A ‘metaphysics’ of mathematics, frequently invisible to the mathematician yet expressed in his writings and teaching in ways more subtle than simple declarative sentences, has existed and can be uncovered in historical research or becomes apparent in mathematical controversy,” e.g., in the case of Eugen Dühring, who in 1887 accused some of his colleagues of engaging in mysticism because they accepted the concept of imaginary numbers (apparently, something persistently hard to swallow for some members of the mathematical community, from Pythagoras on!). Accusations of pseudoscience — some founded, others not — also fly around scientific circles, as for instance in a notorious case where geneticist Michael Lynch (2007) labelled colleagues who take a different approach to certain conceptual issues in evolutionary theory as no better than Intelligent Design creationists [26]. Further, “the fame of the creator of a new mathematical concept has a powerful, almost a controlling, role in the acceptance of that mathematical concept, at least if the new concept breaks with tradition.” And so it goes in science. The already cited Lee Smolin (2007), for instance, has produced a fascinating philosophical, historical and even sociological analysis of the development of string theory in fundamental physics throughout the latter part of the 20th century. From it, Smolin concludes that the impact of a small number of highly influential people, and not just the inherent merits of the theory, has swayed (at least temporarily) an entire discipline into placing most of its conceptual eggs into one approach to the next fundamental theory, with the result that a whole generation of physicists has passed without a new empirically driven breakthrough [27], the first time such a thing has happened in at least a century.

Crowe also maintained that “multiple independent discoveries of mathematical concepts are the rule, not the exception,” recalling that complex numbers, for instance, were discovered (or where they invented?) independently by eight mathematicians, using two different methods. This type of convergent intellectual evolution is certainly not alien to the history of the natural sciences as well, just think of the spectacular case of the simultaneous independent discovery of the theory of natural selection by Charles Darwin and Alfred Russell Wallace (Wilson 2013). And finally: “Mathematicians have always possessed a vast repertoire of techniques for dissolving or avoiding the problems produced by apparent logical contradictions and thereby preventing crises in mathematics ... Revolutions never occur in mathematics.” This is the already discussed point about the fact that a straightforward Kuhnian historiography of mathematics doesn’t work very well (it arguably doesn’t work all that well for much science outside of physics either). More specifically, mathematicians from Fourier to Moritz have remarked that mathematics makes progress slowly, and does so by continuously building on previous knowledge, not by replacing it. The standard example is Euclidean geometry which, contra popular perception, has not been replaced, but rather enlarged and complemented, by non- Euclidean approaches.

A few years after the original article, Crowe (1988) — who must have a penchant for decalogues — commented on what he considers ten misconceptions concerning mathematical practice. Again, several of his points are worth examining briefly, for the insight they provide into matters related to the idea of progress in mathematics, and hence our general quest to understand progress in disciplines that I consider allied to philosophy. Crowe begins by rejecting the common understanding that “the methodology of mathematics is deduction,” contra Hempel (1945/1953), who argued in the positive.

Interestingly, later in his career Hempel himself (1966) published a simple proof that shows that deduction cannot be the sole method of mathematical reasoning, because deduction can only test the validity of a claim, it cannot, unaided, provide a method of discovery. It is also not the case that mathematics provides certain knowledge, according to Crowe, who again cites Hempel (1945/1953) and his demonstration that Euclidean geometry lacks a number of postulates that are actually necessary to prove several of its own propositions, an inconvenient fact that was not discovered for a couple of millennia.

That mathematics is cumulative is another generalization to which Crowe finds plenty of exceptions. While largely true (as is the case for science), it is not difficult to find counterexamples, such as the sidelining of the quaternion system (see above). To complicate matters, however, Quaternions have not in fact been shown to be an incorrect approach, and accordingly they are still used alongside a number of other techniques — for instance in calculations pertinent to 3D rotations, with applications in computer graphics (Goldman 2011). It is also not true that mathematical statements are invariably correct. A good example here is the work by Imre Lakatos (1963/1964) in his Proofs and Refutations, where he shows that one of Euler’s claims for polyhedra [28] has been falsified a number of times and that several proofs of the claim have been shown to have flaws. (For additional discussion of this point see also Philip Kitcher’s (1985) The Nature of Mathematical Knowledge.)

We have already encountered another misconception about mathematics, that its structure accurately reflects its history. This is clearly not true also in the case of science, and it once again relates to the difference between the actual development of a field and the way it is presented in textbooks (i.e., cleaned up and somewhat “mythified”). Crowe remarks, for instance, that most current presentations of mathematical problems begin with axiomatizations, which in reality tend to be achieved late in the development of our understanding of a particular problem. Let’s remember that Whitehead and Russell (1910) took 362 pages to prove that 1+1=2, a mathematical fact that was known for a long time before their Principia Mathematica saw the light. Relatedly, it is not the case that mathematical proof in unproblematic either. Here Crowe quotes none other than Hume (1739/40): “There is no ... mathematician so expert ... as to place entire confidence in any truth immediately upon his discovery of it, or regard it as any thing, but a mere probability. Every time he runs over his proofs, his confidence encreases; but still more by the approbation of his friends; and is rais’d to its utmost perfection by the universal assent and applauses of the learned world.” A well known case is Bell’s (1945) point that Euclid’s original proofs of his theorems have over time been demolished and completely replaced by better ones. Lakatos (1978) defined proofs as “a thought-experiment — or ‘quasi- experiment’ — which suggests a decomposition of the original conjecture into sub- conjectures or lemmas, thus embedding it in a possibly quite distant body of knowledge.” Accordingly, Lakatos encouraged mathematicians to search for counterexamples to accepted theorems, as well as not to abandon apparently refuted theorems too soon. This is all very much reminiscent of the sort of objections to naive falsificationism in natural science stemming from the Duhem-Quine thesis (Ariew 1984), and which we have seen in the last chapter were directly addressed by Lakatos himself.

A misconception cited by Crowe that is crucial for our discussion here (and that goes somewhat against his broad position as stated in the 1975 paper) is that the methodology of mathematics is radically different from the methodology of science. Take Christiaan Huygens’ argument that mathematicians use the same hypothetico-deductive method that is attributed to science, contending that axiom systems are accepted (at least initially) because they are helpful or interesting, not as deductive justifications of theorems. In a very important sense, then, things like non-Euclidean geometries and complex numbers should be thought of as “hypotheses” that mathematicians provisionally embraced and later tested, in the logical equivalent of what physicists do with empirically testable hypotheses. Perhaps Kitcher (1980) put it most clearly: “Although we can sometimes present parts of mathematics in axiomatic form ... the statements taken as axioms usually lack the epistemological features which [deductivists] attribute to first principles. Our knowledge of the axioms is frequently less certain than our knowledge of the statements we derive from them ... In fact, our knowledge of the axioms is sometimes obtained by nondeductive inference from knowledge of the theorems they are used to systematize.” A related questionable notion is that — unlike scientific hypotheses — mathematical claims admit of decisive falsification. There are examples (for instance concerning complex numbers) of apparently falsified claims that were successfully rescued by modifying other aspects of the web of mathematical knowledge, in direct analogy with Quine’s concept of a web of belief for the empirical sciences, which we have discussed in Chapters 2 and 3.

The final misconception tackled by Crowe is that the choice of methodologies used in mathematics is limited to empiricism, formalism, intuitionism, and Platonism. Here he makes a distinction between the (descriptive) history of mathematics and the (perhaps more prescriptive) philosophy of mathematics. In analogy with historically-minded philosophers of science (a la Kuhn) he suggests that the actual practice of mathematics as it has unfolded over the millennia is more messy and complex than it can be accounted for by any single one of the above mentioned categories.

Our brief analysis of how mathematics works is far from comprehensive, and the interested reader is directed to some of the much more in-depth treatments mentioned in the references. But a few general lessons can, I think, be safely drawn. First and foremost, there is no accounting for how mathematics makes progress without paying attention to the history of the field, as reconstructed by actual historians — as opposed to the sanitized, almost mythologized, version one often finds in textbooks. Second, mathematics is neither completely different in nature from, nor is it quite the same as, natural science. For instance, as we have seen argued on several occasions, simple falsification fails in both areas, and for similar, Duhem-Quine related, reasons. Moreover, it is also not true — contra popular perception — that mathematics proceeds by deduction only, leaving the more messy inductive processes to the empirical sciences. But it is certainly the case that deduction plays a much more significant role in mathematics than in the sciences, which do not have anything analogous to the idea of proving a theorem. Also, while we have seen that it is naive to think that once a mathematical truth has been proven it is done with, contributing to a monotonic, relentless increase in mathematical knowledge, it is the case that the paths taken by the natural sciences are much more untidy and prone to reversal — precisely because they depend substantially on empirical evidence and cannot rely on deductive proof [29].

The overall picture that emerges, then, is one in which there are both significant similarities and marked differences between the natural sciences and mathematics, which have consequences for our understanding of how the two make progress. I turn now for the rest of the chapter to the field of logic, where we will see fewer similarities with the natural sciences and more with mathematics, and that will help us further bridging the gap toward a reliable concept of progress in philosophy, the focal topic of the next chapter.

Logic: the historical perspective

In the case of logic, too, a bit of a historical perspective will help making the case for how the field has, unquestionably, made progress, albeit differently from both the situations we have already explored in the cases of the natural sciences and of mathematics. To get us started, let us see if we can get clearer about what it is that defines the subject matter we are now tackling. According to Bird (1963) most authors agree that logic is concerned with the structure of propositions, independently of content, and Kneale (cited in Bird, p. 499) puts it this way: “[logic consists in] classifying and articulating the principles of formally valid inference” (which puts logic, at the least in part, in the business of carrying out normative analyses of human reasoning, as opposed to, say, the sort of descriptive picture we get from psychological studies of cognitive biases: Caverni et al. 1990; Pohl 2012). As we shall see in the next section, there actually are some exceptions to this general idea, but broadly speaking that is a good definition of the object of study of logicians.

Logic originated (and, to a point, evolved) pretty much independently in two places: Greece and India, and we will see that Indian logicians discovered (or invented) many of the same principles that are familiar to us from Greek logic, a pattern that we readily expect in the natural sciences, but that we have seen takes place also in mathematics. Nonetheless, Bird argues that progress in logic has not followed a linear trajectory, citing Bochenski (p. 494) as proposing a framework for understanding the history of (Western) logic that roughly speaking recognizes three “high points”: Aristotelian and Stoic ancient logic; Medieval Scholastic logic; and modern mathematical logic. I will get to some of the details below, but before proceeding let me follow King and Shapiro (1995) in providing a general panorama that I hope will be helpful to properly situate much of the rest of this chapter.

They begin with the ancient Greeks, crediting Aristotle both with the invention of syllogistics and of essential so-called “metalogical” theses: the Law of Bivalence, the Law of Noncontradiction, and the Principle of the Excluded Middle. After Aristotle and the Stoics, the first major innovator was Peter Abelard (12th century), most notably because of his formulation of relevance criteria for logical consequences. In the 14th century Jean Buridan, Albert of Saxony and William of Ockham were among those who helped develop supposition theory. We then jump to the 19th century, when Bolzano elaborated important new notions, such as those of analyticity and logical consequence. By the end of that century, according to King and Shapiro, we can distinguish a trifurcation of approaches in modern logic: (i) the algebraic school (exemplified by Boole and Venn), interested in developing calculi for reasoning, such as the one nowadays referred to as Boolean algebra, which has had countless applications in computer science; (ii) the logicist school (Frege and Russell, among others), aiming at codifying the general features of precise discourse within a single system. Famously, it was Russell (through the discovery of his namesake paradox) that managed to undermine Frege’s project of showing that arithmetic is a part of logic; and (iii) the mathematical school (e.g., Hilbert, Peano, Zermelo), attempting to axiomatize branches of mathematics, like geometry and set theory. Contemporary research in logic is a mixed blend of these three general tendencies, and has yielded plenty of fruits: work on meta-mathematics, culminating in Gödel’s incompleteness theorems; Alfred Tarski’s work on definitions of truths and logical consequence; and Alonzo Church’s demonstration that there is no algorithmic way to show that a given first-order formula is a logical truth, to mention just a few examples. Moreover, mathematical logic has provided the underlying structure for modern work in analytic philosophy, on which I will touch briefly below, including the contributions of authors like Davidson, Dummett, Quine, and Kripke.

With this broad vista in mind, let us take a closer look at three specific periods of development of logic, two in the Western world (ancient and medieval logic), the third one in India, so to better be able to appreciate the dynamics of progress in the field, as well as how they differ from what we have seen so far. Arguably, the beginning of logic took place once people started to think about the patterns of arguments, paying attention to their formal grammar (Bobzien 2006). Among the ancient Greeks, Zeno of Elea and Socrates used essentially what today are known as reductio arguments, though they took them for granted, without exploring their logical structure, while Eubulides originated a number of well known paradoxes, starting with the Liar and Sorites ones. Both the sophists and Plato were interested in logic and in fallacies of reasoning, and Plato makes an early distinction between syntax and semantics, i.e. between asking what a statement is and when that statement is true.

Following Bobzien (2006; but see also: Kapp 1942; Kneale and Kneale 1962; Lear 1980), Aristotelian logic — certainly the turning point in the Western history of the field — shares elements in common with both predicate logic and set theory, though Diodorus Cronus, his student Philo, and later the Stoic Chrysippus developed a different approach to logic, which turns out to have similarities with the much later work of Frege. Aristotle’s Topics (which is part of his Organon, the target of the famous criticism by Francis Bacon, many centuries later) is the first complete treatise on logic, while his Sophistical Refutation is the first formal analysis of logical fallacies, building, presumably, on the early treatment by his mentor, Plato. Without question Aristotle’s most enduring contribution to logic, lasting well into the 19th century, was his detailed analysis of syllogisms — which was later commented upon and refined throughout the Middle Ages. And it was again Aristotle who invented modal logic, where the predicate holds actually, necessarily, possibly, contingently or impossibly.

Even before getting to the often unjustly under-appreciated (at least in popular lore) medieval logicians, the Aristotelian system was improved and refined by a number of people, including Theophrastus (who was a student of Aristotle) and Eudeumus, who pointed out that in modal logic the conclusion must have the same modal character of the weaker premise. These same authors also introduced what amounts to the forerunners of modern day modus ponens and modus tollens. The Stoics, such as Chrysippus of Soli, seem to have endorsed a type of deflationary view of truth, and were particularly interested in the “sayables” — i.e., in whatever underlies the meaning of everything we think. A subset of sayables is constituted by the so-called assertibles, which are characterized by truth values. The assertibles are the smallest expressions in a deductive system, and including them in one’s logic gives origin to a system of propositional logic in which arguments are composed of assertibles. The Stoics also developed a system of syllogisms, and they recognized that not all valid arguments are syllogisms. Their syllogistics, however, is different from Aristotle’s, and has more in common with modern day relevance logical systems. These two traditions in Greek logic, the so-called “Peripatetic” (i.e., Aristotelian) and Stoic were brought together by Galen in the 2nd Century, who made a first (and largely incomplete) attempt at synthesizing them. Stoic logic, however, pretty much disappeared from view by the 6th century CE, to eventually re-emerge only during the 20th century because of renewed interest in propositional logic.

Following Lagerlund (2010), the history of medieval logic is divided into “old logic” and “new logic,” separated by the figure of Abelard (12th century CE). This is because until Abelard’s time logicians only had access to parts of Aristotle’s works, which excluded the Prior Analytics, the book in which Aristotle developed his theory of syllogisms, although people knew about his theory from secondary sources. Aristotle’s theory was an impressive achievement, but was incomplete, and we owe its fuller development to the medieval logicians. In particular, Aristotle employed two methods to jointly prove validity in syllogistic theory (reductio ad impossibile and ekthesis [30]), and it was Alexander of Aphrodisias (c. 200 AD) who first showed that ekthesis was by itself sufficient for the purpose. The “old logic” period begins with Boethius (6th century CE), who provided a presentation of syllogistic theory that was clearer than Aristotle’s own (though anyone familiar with Aristotle’s work will testify that that particular bar is set a bit low). Boethius did make a few novel contributions, the main one of which was his introduction of the hypothetical syllogism, i.e., a syllogism in which one (or more) of the premises is a hypothetical, rather than a categorical sentence.

We then have to wait another six centuries — underscoring the fact that logic, more so even than mathematics, certainly doesn’t make progress in anything like a linear or steady fashion — for Abelard to clarify and improve on Boethius’ work and also to introduce the famous distinction between de dicto and de re modal sentences. The idea is that a sentence such as “Massimo necessarily has to write” can be interpreted in two ways: “Massimo writes necessarily” or “It is necessary that Massimo writes.” The difference is between a personal and an impersonal reading of the original sentence, and Abelard pointed out that the distinct meanings of modal sentences should be kept in mind, because attributes such as quantity and quality hold differently depending on the modal meaning. One of Abelard’s main contributions was the beginning of a theory of consequences, which later on during medieval times replaced syllogistic theory as the main interest of logicians.

Again following Lagerlund (2010; see also: Lagerlund 2000; Zupko, 2003; Dutilh-Novaes 2008), Richard of Campsall (14th century CE) provided a complex rendition of syllogistic theory, which ended up implicitly showing that a consistent interpretation of Aristotle’s Prior Analytics is actually not possible. This in turn led William of Ockham to take the extraordinary step of simply abandoning Aristotle’s approach to seek a more systematic account of syllogistic theory. But it was John Buridan who showed that syllogistic theory is in fact a special case of a more general theory of consequences. His work achieved the most complete account of modal logic available at the time, and by implication the most powerful system of logic devised within the Western canon before the modern era, with some modern commentators even arguing that Buridan’s system was developed by thinking in terms of a (very contemporary) “possible worlds” model — though recall the warning given above about unwisely lapsing into a heritage view of history.

The reader may have noticed that I have used several times the term “development” to describe the above sequence of discoveries (or inventions) in Western logic. That term seems to me to best capture the sense in which logic makes progress: not by accumulating truths about the world (a la natural science), but — similar to mathematics — by becoming more and more explanatory in response to largely internally generated problems. This is, again, not teleonomic progress toward an end goal, or overarching theory of everything, but expansion by multiplicative exploration of novel areas of conceptual space — areas that, to use Smolin’s terminology introduced at the beginning of the book, are progressively “evoked” once logicians adopt new axioms and build new systems. This will appear even more obviously to be the case below, once we get to the panoply of contemporary logics (plural).

Our third glance at some of the details of the history of logic turns east, toward the parallel development of the field in the Indian tradition (for an overview see: Matilal 1998; Ganeri 2001; Gillon 2011; see also Chapter 2). Here the early Buddhist literature already mentions debates and other forms of public deliberation in ancient India, suggesting an early interest in the art of reasoning similar to the one developed independently in ancient Greece. Buddhist writers from the 3rd century BCE were aware that the form of an argument is crucial to the argument being a good one. Moreover, we have texts that document Indian logicians’ familiarity with a number of forms of reasoning that are equivalent to several of those developed in the West, including modus tollens, modus ponens, and reductio ad absurdum. The principle of non-contradiction was not studied explicitly, but was often implicitly invoked (e.g., by the Buddhist philosopher Nāgārjuna in the 2nd century CE). At about the same time Gautama wrote Nyāya-sūtra (Aphorisms on Logic), an early treatise on inference and logic, and a bit later (6th century CE) Bhartṛhari formulated a version of the principle of the excluded middle.

Even before Bhartṛhari, Vātsyāyana (5th century CE) rejected similarity and dissimilarity (i.e., arguments from analogy) as underlying syllogisms, proposing instead a view of syllogism that invokes the concept of causation. While this was far from a complete account, it demonstrates a very clear understanding of the problem of syllogistic soundness. Dignāga (c. 5th–6th century CE) then made the connection between inference and argument, treating them as two aspects of the same reasoning process, although according to Gillon (2011) he seemed to be confused about the role of examples in syllogisms (he thought they were necessary, and they are not, they are just illustrative). That confusion apparently stemmed from a deeper one: failing to make a sharp distinction between validity and persuasiveness (examples are crucial to the latter — as any good lawyer will tell you — but irrelevant to the former).

One of Dignāga’s students, Is̄ ́varasena, seems to have been the first to recognize the problem of induction (which was not formulated explicitly in the West until Hume in the 18th century!), though his solution of it (invoking non-perception of the first premiss) was inadequate (as pretty much any other solution proposed thus far, I might add). One of his students, Dharmakir̄ ti (7th century CE), in turn tried his hand at solving the problem by arguing that the truth of the first premiss is guaranteed by causal relations or by identity. The story could continue with a number of other convergences and parallels with the history of Western logic, but I think that the examples given above clearly affirm that logical principles were arrived at in both India and the West, and that the field made progress — in the sense clarified above — for centuries before the modern era, albeit of course at different paces between East and West, and with partially different focus and approaches. Let’s now turn from history to examine what contemporary logic as a field of scholarship looks like. It will be immediately clear that the telltale signs are the same: diversification and non-teleonomic progress interpreted as continuously expanding explanatory power with regard to internally generated problems.

A panoply of logics

The striking thing about contemporary logic is that it is plural. Indeed, Logics (Nolt 1996) was the title of the book I used as a graduate student at the University of Tennessee, and that in itself was a surprise for me, since I had naively always thought of logic as a single, monolithic discipline. (But why, really? We have different ways of doing geometry and mathematics, and certainly a plethora of natural sciences!). The following brief look at modern logic should be enough to convince readers that the field is both vibrant and progressive, in the sense discussed above.

Consider, for instance, modal logic (Garson 2009), which deals with the behavior of sentences that include modal qualifiers, such as “necessarily,” “possibly,” and so on. It is actually a huge field within logic, as it includes deontic (“obligatory,” “permitted,” etc.: Hilpinen 1971), temporal (“always,” “never”), and doxastic (“believes that”) logics. Arguably the most familiar type of modal logic is the so-called K-logic (named after influential 20th century philosopher Saul Kripke), which is a compound logical system made of propositional logic, a necessitation rule (using the operator “it is necessary that”) and a distribution axiom. A stronger system, called M, is built by adding the axiom that whatever is necessary is the case, and this in turn yields an entire family of modal logics with different characteristics. Starting again with K-logic, one can also begin to build a deontic logic by adding an axiom that states that if x is obligatory, then x is permissible.

Similarly, one can build temporal logics (with the details depending on one’s assumptions about the structure of time) and other types of modal logics. Indeed, Garson (2009) presents an elegant “map” of the relationships among a number of modal logics, demonstrating how they can all be built from K by adding different axioms. Furthermore, Lemmon and Scott (1977) have shown that there is a general parameter (G) from the specific values of which one can derive many (though not all) the axioms of modal logic. Garson’s connectivity map and Lemmon and Scott’s G parameter are both, well, highly logical, and aesthetically very pleasing, at the least if you happen to have a developed aesthetic sensibility about logical matters. (Notice, once again, that these are all nice examples of non-teleonomic progress propelled by internally generated problems and consisting in exploring additional possibilities in a broad conceptual space that is evoked once one adds axioms or assumptions.)

A major issue with modal logic is that — unlike classical logic (Benthem 1983) — it is not possible to use truth tables to check the validity of an argument, for the simple reason that nobody has been able to come up with truth tables for expressions of the type “it is necessary that” and the like. The accepted solution to this problem (Garson 2009) is the use of possible worlds semantics (Copeland 2002), where truth values are assigned for each possible world in a given set W. Which implies that the same proposition may be true in world W1, say, but false in world W2. Of course one then has to specify whether W2, in this example, is correctly related to W1 and why. This is the sort of problem that has kept modal logicians occupied for some time, as you might imagine. Modal logic has a number of direct philosophical applications, as in the case of deontic logic (McNamara 2010), which deals with crucial notions in moral reasoning, such as permissible / impermissible, obligatory / optional, and so forth. Deontic logic has roots that go all the way back to the 14th century, although it became a formal branch of symbolic logic in the 20th century. As mentioned, deontic logic can be described in terms of Kripke-style possible worlds semantics, which allows formalized reasoning in metaethics (Fisher 2011).

Of particular interest, but for different reasons, are also the next two entries in our little catalog: many-valued and “fuzzy” logics. The term many-valued logic actually refers to a group of non-classical logics that does not restrict truth values to two possibilities (true or false; see Gottwald 2009). There are several types of many-valued logics, including perhaps most famously Łukasiewicz’s and Gödel’s. Some of these admit of a finite number of truth values, others of an infinite one. The Dunn/Belnap’s 4-valued system, for instance, has applications in both computer science and relevance logic. Multi-valued logic also presents aspects that reflect back on philosophical problems, as in the area of concepts of truth (Blackburn and Simmons 1999), or in the treatment of certain paradoxes (Beall 2003), like the heap and bald man ones. More practical applications are found in areas such as linguistics, hardware design and artificial intelligence (e.g., for the development of expert systems), as well as in mathematics. Fuzzy logic is nested within many-valued logics (Zadeh 1988; Hajek 2010), consisting of an approach that makes possible to analyze vagueness in both natural language (about degrees of beauty, age, etc.) and mathematics. The basic idea is that acceptable truth values range across the real interval [0,1], rather than lying only at the extremes (0 or 1) of that interval, as in classical logic. Fuzzy logic deals better than two-valued logic with the sort of problems raised by Sorites paradox, since these problems are generated in situations in which small/large, or many/ few quantifiers are used, rather than simple binary choices. Therefore, fuzzy logic admits of things being almost true, rather than true, and it is for this reason that some authors have proposed that fuzzy logic can be thought of as a logic of vague notions.

A whole different way of thinking is afforded by so-called intuitionistic logic (Moschovakis 2010), which treats logic as a part of mathematics (as opposed to being foundational to it, as in the old Russell-Whitehead approach that we have discussed above), and — unlike mathematical Platonism (Linnebo 2011) — sees mathematical objects as mind-dependent constructs. Important steps in the development of intuitionistic logic were Gödel’s (who, ironically, was a mathematical Platonist!) proof (in 1933) that it is as consistent as classical logic, and Kripke’s formulation (in 1965) of a version of possible-worlds semantics that makes intuitionistic logic both complete and correct. Essentially, though, intuitionistic logic is Aristotelian logic without the (much contested) law of the excluded middle, which was developed for finite sets but was then extended without argument to the case of infinities.

Finally, a couple of words on what some consider the cutting edge, and some a wrong turn, in contemporary logic scholarship: paraconsistent and relevance logics. Paraconsistent logic is designed to deal with what in the context of classical logic are regarded as paradoxes (B. Brown 2002; Priest 2009). A paraconsistent logic is defined as one whose logical relations are not “explosive,” [31] with the classical candidate for treatment being the liar paradox: “This sentence is not true.” The paraconsistent approach is tightly connected to a general view known as dialethism (Priest et al. 2004), which is the idea that — contra popular wisdom — there are true contradictions, as oxymoronic as the phrase may sound. Paraconsistent logic, perhaps surprisingly, is not just of theoretical interest, as it turns out to have applications in automated reasoning: since computer databases will inevitably include inconsistent information (for instance because of error inputs), paraconsistent logic can be deployed to avoid wrong answers based on hidden contradictions. Similarly, paraconsistent logic can be deployed in the (not infrequent) cases in which people hold to inconsistent sets of beliefs, sometimes even rationally so (in the sense of instrumental rationality). More controversially, proponents of paraconsistent logic argue that it may allow us to bypass the constraints on arithmetic imposed by Gödel’s theorems. How does this work? One approach is known as “adaptive logic,” which begins with the idea that consistency is the norm, unless proven otherwise, or alternatively that consistency should be the first approach to a given sentence, with the alternative (inconsistency) being left as a last resort. That is to say, classical logic should be respected whenever possible. Paraconsistent logics can be generated using many-valued logic, as shown by Asenjo (1966), and the simplest way to do this is to allow a third truth value (besides true and false), referred to as “indeterminate” (i.e., neither true nor false).

Yet another approach within the increasingly large family of paraconsistent logics it to adopt a form of relevance logic (Mares 2012), whereby one stipulates that the conclusion of a given instance of reasoning must be relevant to the premises, which is one way to block possible logical explosions. According to relevance logicians what generates apparent paradoxes is that the antecedent is irrelevant to the consequent, as in: “The moon is made of green cheese. Therefore, either it is raining in Ecuador now or it is not,” which is a valid inference in classical logic (I know, it takes a minute to get used to this). The typical objection to relevance logic is that logic is supposed to be about the form, not the content, of reasoning — as we have seen when briefly examining the history of both Western and Eastern logic — and that by invoking the notion of “relevance” (which is surprisingly hard to cash out, incidentally) one is shifting the focus at least in part to content. Mares (1997), however, suggests that a better way to think about relevance logic comes with the realization that a given world X (within the context of Kripe-style many worlds) contains informational links, such as laws of nature, causal principles, etc. It is these causal links, then, that are deployed by relevance logicians in order to flesh out the notion of relevance (in a given world or set of possible worlds) — perhaps reminiscent of Dharmakīrti’s invoking of causal relations to assure the truth of a first premiss, as we have discussed. Interestingly, some approaches to relevance logic (e.g., Priest 2008) can be deployed to describe the difference between a logic that applies to our world vs a logic that applies to a science fictional world (where, for instance, the laws of nature might be different), but relevance logic has a number of more practical applications too, including in mathematics, where it is used in attempts at developing mathematical approaches that are not set theoretical, as well as in the derivation of deontic logics, and in computer science (development of linear logic).

So, what do we get from the above historical and contemporary overviews of logic, with respect to how the field makes progress? The answer is, I maintain, significantly different from what we saw for the natural sciences in Chapter 4, but not too dissimilar from the one that emerged in the first part of this chapter in the case of mathematics. Logicians explore more and more areas of the conceptual space of their own discipline. Beginning, for instance, with classical two-valued logic it was only a matter of time before people started to consider three-valued and then multi-valued, and finally infinitely-valued (such as fuzzy) types of logical systems. Naturally enough, this progress was far from linear, with some historians of logic identifying three moments of vigorous activity during the history of Western logic, with the much maligned Middle Ages not devoid of interesting developments in the field. Other signs of progress can readily be seen in the expansion of the concerns of logicians, beginning with Aristotelian syllogisms or similar constructs (as in the parallel developments of the Stoics) and eventually exploding in the variety of contemporary approaches, including deontic, temporal, doxastic logics and the like. Even dialethism and the accompanying paraconsistent and relevance logics can be taken as further explorations of a broad territory that began to be mapped by the ancient Greeks: once you chew for a while (in this case, a very long while!) on the fact that classical logic can yield explosions and paradoxes, you might try somewhat radical alternatives, like biting the bullet and treating some paradoxes as “true,” or pushing for the need for a three- valued approach when considering paradoxes. As in the case of mathematics, there have been plenty of practical (i.e., empirical) applications of logic, which in themselves would justify the notion that the field has progressed. But in both mathematics and logic I don’t think the empirical aspect is quite as crucial as in the natural sciences. In science there is a good argument to be made that if theory loses contact with the empirical world (Baggott 2013) then it is essentially not science any longer. But in mathematics and logic that contact is entirely optional as far as any assessment of whether those fields have been making progress by the light of their own internal standards and how well they have tackled the problems that their own practitioners set out to resolve.

What about philosophy, then? It is finally to that field that I turn next, examining a number of examples of what I think clearly constitutes progress in philosophical inquiry. As we shall see, however, the terrain is more complex and perilous. More complex because while philosophy is very much a type of conceptual activity, sharing in this with mathematics and logic, it also depends on input from the empirical world, both in terms of commonsense and of scientific knowledge. More perilous because a relatively easy case could be made that a significant portion of philosophical meanderings aren’t really progressive, and some even smack of mystical nonsense. Unfortunately, this sort of pseudo-philosophy does appear in the philosophical literature, side by side with the serious stuff, and occasionally is even the result of the writings of the same authors! Nothing like that appears to be happening either in science or in mathematics and logic, which I believe is a major reason why philosophy keeps struggling to be taken seriously in the modern academic world.

6. Progress in Philosophy

“What is your aim in Philosophy? To show the fly the way out of the fly-bottle” (Ludwig Wittgenstein)

We finally get to the crux of the matter: how does philosophy make progress? By now we should have a more nuanced appreciation of a number of concepts of progress in what I think are the most closely allied disciplines to philosophy: the natural sciences, mathematics, and logic. I actually happen to think that other fields in the humanities also make progress, in the sense of developing by exploration of an internally generated conceptual space whose characteristics are “evoked” (see Introduction) once certain assumptions or starting parameters are in place. These include perhaps most obviously history, and more controversially literary and art criticism. But those fields are too far afield of my technical purview to treat in any detail here, so I will leave that task to others who are better suited to carrying it out.

I will proceed, as it has been the case during most of our discussion, by example, counting on the idea that the contours of the broader picture will emerge as we go along (a Wittgensteinian approach, if you will). As it should be clear by now, I think it is a mistake to tackle complex problems by providing sharp, necessary-and-sufficient type, definitions. Human intellectual endeavors are just too intricate and nuanced for that sort of approach. The examples I will draw on below are from areas of philosophy I am more familiar with — either because I actually worked on them or because they interest me in some special fashion. Which means that the selection of examples should not be taken as exhaustive, and is certainly only partially representative of the huge and highly diverse field of philosophy (Chapter 2). This very same chapter would have been written substantially differently by another philosopher with a different range of expertise and interests, but that should not affect the basic message that, I hope, will come through loud and clear.

Progress in conceptual space — which is the way I am thinking of progress in philosophy in general — can occur because of the discovery of new “peaks,” corresponding to new intellectual vistas to be explored and eventually refined; or because of the realization that some ideas are actually “valleys,” i.e. they need to be mapped so that we know they exist and what they look like, but then also discarded so not to impede further progress (recall our discussion of Rescher’s aporetic clusters in the Introduction). An objection that can be raised to my approach is that progress necessarily entails a teleonomic component, the idea that a field is “going somewhere,” so to speak, whereas I am defining progress in philosophy (and, similarly, in mathematics and logic) as the process of finding new places to go, largely in response to internally generated problems. As it should be clear by this point, however, I think that a teleological view of progress is only one of a number of possible conceptualizations of the idea of progress, one that fits particularly well the scientific context. Still, I doubt many people would deny that mathematics and logic also make progress, and yet these cases — I suggest — are not teleological. If so, the choice for the critic is either to maintain a narrow, necessarily teleological view of progress and deny that mathematics and logic make progress, or to accept that those fields make progress and so discard the teleological requirement as necessary (although it may be sufficient, in specific instances).

Now, we have already encountered a number of “valleys” in philosophy’s conceptual landscapes. Take, for instance, the most extreme postmodernist attacks on science (Chapters 1 and 2), Jerry Fodor’s misguided criticism of Darwinism (Chapter 1), and Thomas Nagel interesting but ultimately dead-ended challenge to naturalism (Chapter 1). And that list could be much, much longer. What follows, by contrast, is a series of sketches of how philosophers positively build (discover? Invent?) positive peaks within three areas of the vast landscape in which they move: epistemology, philosophy of science, and ethics. Once again, what we are about to embark on is nothing like an exhaustive survey of those fields of philosophical inquiry, and indeed I will only be in a position to comment briefly on each of the specific examples (despite the length of this chapter). The objective here is to provide a flavor of what it means to make progress in philosophy by sampling different areas of scholarship within its broader domain. Hopefully, others will be able to elaborate on this sketch and add many more such examples. It’s about time that philosophers stop shooting themselves in the foot (Chapter 1) and realize that they have nothing to envy to other fields in terms of rigor of their investigations and soundness of their results.

Knowledge from Plato to Gettier and beyond

“Knowledge” is a heterogeneous category: I may “know,” for instance, my friend Phil; or how to cook risotto; or that I am in pain. But as far as epistemology is concerned, we are talking about knowledge of propositions, something along the lines of “S knows that p” (Steup 2005). The traditional view in epistemology dates back to Plato and consists in the idea that knowledge requires three components, which are individually necessary and jointly sufficient: justification, truth, and belief (JTB, for short — though it isn’t exactly clear the extent to which Plato himself endorsed such view). During the second part of the 20th century, however, a family of non-traditional views began to be developed, stemming from a class of objections that show the JTB account of knowledge to be incomplete. These are known as Gettier (1963) cases.

The exploration of this particular peak (really, more like a mini-mountain range) in conceptual space began with the publication of a short paper (three pages) published by now retired University of Massachusetts at Amherst’s Edmund Gettier back in 1963 (as it turns out, he wrote it in order to get tenure, and it is the only paper he published in his entire philosophical career — not exactly a pattern that fits with the contemporary bean counting obsession of university administrators). So to better follow this first example, and to properly visualize what I mean by conceptual space, I have drawn a concept map (Moon et al. 2011; Kinchin 2014) to help us along (Figure 4). Beginning on the left side of the concept map, we start with the “Platonic” definition of knowledge as Justified True Belief. This means that for something to count as knowledge, the epistemic agent’s belief about a certain matter has to be both true and (rationally) justified. For instance, let’s say you believe that the earth goes around the sun, rather than the other way. This belief is, as far as we can tell, true. But can you justify it? That is, if someone asked you why you hold that particular belief, can you actually give an account of it? If yes, congratulations, you can say that you know (in the Platonic sense) that the earth goes around the sun. Otherwise you are simply repeating something you heard or read somewhere else.

(Which, of course, is fine from a pragmatic perspective. It just doesn’t count as knowledge.)

Figure 1: An overview of the conceptual landscape concerned with definitions of knowledge

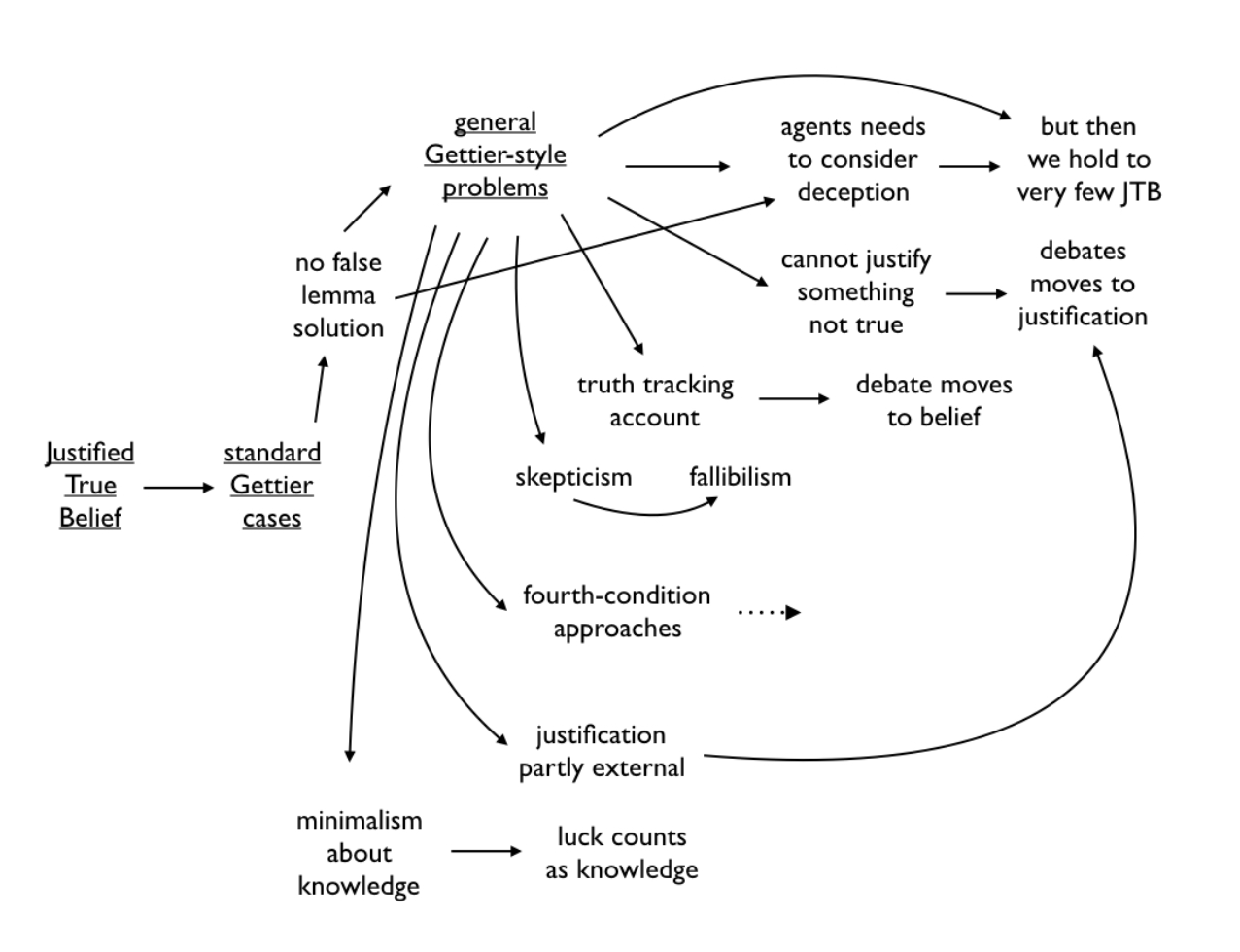
Now, the above approach was good enough for about two and a half millennia, until some people — e.g., Bertrand Russell — began questioning it and thinking about its limitations. But the big splash on the knowledge thing was the short paper by Gettier. Because the problem posed by Gettier may not sound that impressive the first (or even the second) time you encounter it, be sure to take some time to metabolize the issue, so to speak.

A typical “Gettier case” is a hypothetical situation that seems to be an exception to the JTB conception of knowledge. [32] Let’s say I see letters, copies of utilities bills and other documents from my friend Phil, and they all refer to a residence in New York City, state of New York. I would be justified in believing that Phil lives in New York City. If Phil lives in NYC, then it is also true that Phil lives in the State of New York, and consequently I believe that too. Turns out, however, that Phil actually lives on Long Island (he just likes to have his bills sent to New York City, to show off with his friends). So my first belief about Phil was simply wrong. This presents no problem for the JTB account, since my belief only satisfied one of the other two conditions (it was justified, but not true). The trouble comes when we assess my second belief, that Phil lives in the State of New York. I am correct, he does. That belief of mine is both true, and justified (logically, given the premise that Phil lives in NYC). But now we have a case of justified true belief that is actually based on false premises, since Phil does not, in fact, live in New York City.

Gettier cases have the general form of the example I just gave: they get off the ground because they are about inferring conclusions via a belief that is justified but not true. The problem they pose is not with the first belief (the one that is justified but not true) but with the second belief (the one that is inferred from the first one, and which happens to be true). Now what?

The first response — the first move in logical space after Gettier’s own — was for epistemologists to seize on the already noted fact that Gettier cases depend on the presence of false premises and simply amend the definition of knowledge to say that it is justified true belief that does not depend on false premises (the “no false lemma” solution, see concept map). As it turns out, however, one can easily defeat this move by introducing more sophisticated Gettier cases that do not seem to depend on false premises, so called general Gettier-style problems.

Here is one possible (if a bit contrived) scenario: I am walking through Central Park and I see a dog in the distance. I instantly form the belief that there is a dog in the park. This belief is justified by direct observation. It is also true, because as it happens there really is a dog in the park. Problem is, it’s not the one I saw! The latter was, in fact, a robotic dog unleashed by members of the engineering team from the Bronx High School of Science. So my belief is justified (it was formed by normally reliable visual inspection), true (there is indeed a dog in the park), and arrived at without relying on any false premise. And yet, we would be hard pressed to call this an instance of “knowledge.” It looks more like a lucky coincidence.

There is, however, a move that can be made by supporters of the no false lemma solution to repair their argument, which consists in adding that the epistemic agent needs to (consciously or even unconsciously) consider the possibility of both deception and self- deception, claiming knowledge only when those have been ruled out. The problem with that solution is that if we accept it then it turns out that we hold to a lot fewer justified beliefs than we think, perhaps even starting us on the road to complete skepticism.

A related, but distinct, move, is to say that Gettier cases are not exceptions to JTB because it does not make sense to say that one can justify something that is not true. That may be, but this moves the discussion away from the concept of knowledge and onto that of justification, which turns out to be just as interesting and complicated (we’ll get there in a bit).

A completely different take is adopted by philosophers who have tried to “dissolve” rather than resolve the Gettier problem (lower portion of the concept map). Here there are at least two areas of logical space that can be reasonably defended: the minimalist answer is to bite the bullet and agree that all cases of true belief, including accidental ones, count as knowledge. The good news is that we end up having much more knowledge than we thought; the bad news is that it seems we are now counting as “knowledge” the sort of lucky coincidences (see the dog example above) that are really hard to swallow for an epistemologist. A second way of dissolving the Gettier problem is to say that it gets wrong the concept of justification (again, thus shifting the focus of the discussion). For instance, one could say that justification depends not just on the internal state of the epistemic agent, but also on how it relates to the state of affairs in the external world (the dog is really a robot!). This means that we are now owed an account of why there may be a misalignment between internal and external states, or what makes a belief appropriate or inappropriate.

The upper-central portion of my concept map refers to two additional broad categories of replies (two peaks in this particular conceptual space), one that adopts the strategy of revising the JTB approach itself, the second that aims at expanding it with a further, “G” (for Gettier) condition. Let’s start with possible modifications of JTB. One option was suggested by Fred Dretske (1970) and separately by Robert Nozick (1981), and is known as the “truth tracking” account: it basically says that the epistemic agent shouldn’t believe proposition p if p were not true. This, however, immediately leads to the question of what accounts for agents having this or that belief. A second modification of JTB is known as Richard Kirkham’s skepticism, and it is an acknowledgment of the fact that there will always be cases were the available evidence does not logically necessitate a given belief. This move in turn leads to a split: on the one hand, one can simply embrace skepticism about knowledge and be done with it. On the other hand, one can adopt a fallibilist position and agree that a belief can be rational even though it doesn’t rise to the lofty level of knowledge.

We now move to explore the last area (lower-center) of logical space opened up (“evoked,” to use our by now familiar terminology) by discussions of Gettier problems: the so-called “fourth condition” family of approaches (detail in Figure 2). One is represented by Alvin Goldman’s causal theory of belief, which says that it is the truth of a given belief that causes the agent to hold to a belief in the proper manner (an improper manner would fall back into Gettier-style cases). This again raises the issue of how we account for the difference between appropriate and inappropriate beliefs, the very same question raised by one of the dissolution approaches, the one that says that Gettier cases involve a wrong concept of justification, as well as by the Dretske-Nozick response. Goldman himself was happy to proceed by invoking some form of reliabilism about justification.

Figure 2: A subset of the conceptual landscape concerned with the definition of knowledge

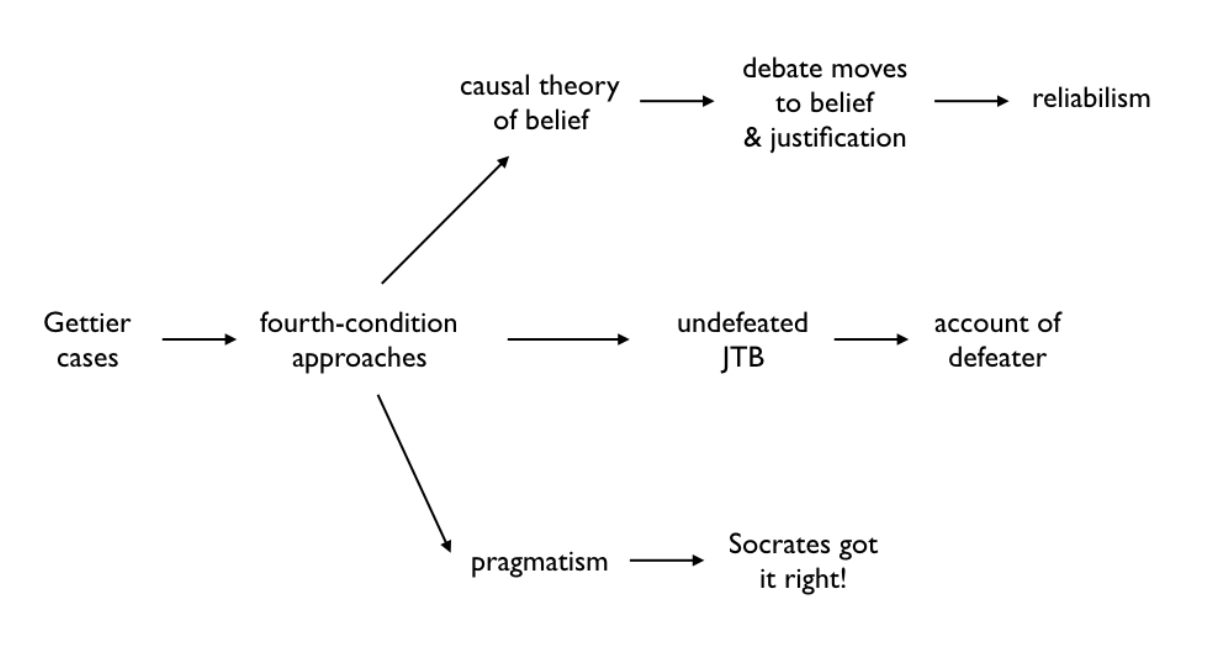
Keith Lehrer and Thomas Paxson have advanced the possibility of defeasibility conditions: knowledge gets redefined as “undefeated” justified true belief. This is not the place to pursue it further, but the problem — as presented by some of Lehrer and Paxson’s critics — is that it is surprisingly hard to get a good grip on the concept of a defeater in a way that doesn’t rule out well established instances of a priori knowledge that we want to preserve, like logical and mathematical knowledge.

Finally, we have the pragmatic move: since truth is defined by pragmatists like Charles Sanders Peirce as the eventual opinion reached by qualified experts, we get that in most ordinary cases of “knowledge” we simply need to embrace a Socratic recognition of our own ongoing ignorance.

Now, you may be thinking: so, after all this, what is the answer to Gettier-style problems? What is the true account of knowledge? If so, you missed the point of the whole exercise. Unlike science (Chapter 4), where we seek answers to questions determined by empirical evidence and we do expect (eventually, approximately) to get the right one, philosophy is in the business of exploring logically coherent possibilities, not of finding the truth. There are often a number of such possibilities, since the constraints imposed by logic are weaker than those imposed by empirical facts. At the end of our discussion of knowledge and Gettier cases, however, we are left with the following: a) A much better appreciation for the complexities of the deceptively simple question: what is knowledge? b) An exploration of several possible alternative accounts of knowledge and related concepts (such as justification and belief); c) A number of options still standing, some of which may be more promising than others; and d) A number of possibilities that need to be discarded because they just don’t work when put under scrutiny. And that, I think, is how philosophy makes progress.

More, much more, on epistemology

There is, of course, much more to be said about epistemology, and as usual the proper SEP entry (an extremely valuable peer reviewed resource that has accompanied us throughout this book) is an excellent starting point for further exploration (in this case, Steup 2005). Before leaving the field to move on to philosophy of science, I want to briefly sketch a number of other debates in epistemology that lend themselves to the same kind of analysis I just went into some detail in the case of the concept of knowledge. I have not drawn concept maps for the remaining examples in this chapter, but doing so is an excellent exercise for the interested reader, both to make sure one is able to reconstruct how the various moves and countermoves are logically connected, and to develop a first-hand feeling for philosophical progress so understood. It will help to think of each position to be briefly examined below as a peak in the proper conceptual landscape, whose height depends on how justified the pertinent position happens to be.

A couple of times already in our preceding discussion we have gotten to the point where we really needed to unpack the idea of justification. As it turns out, much has been written about it. To begin with, epistemologists recognize two major approaches to justification: deontological and non-deontological. Deontological Justification (DJ) looks something like this (Steup 2005): “S is justified in believing that p if and only if S believes that p while it is not the case that S is obliged to refrain from believing that p” — which is how, for instance, Descartes and Locke thought of justification. Non-Deontological Justification (NDJ), instead, takes the form: “S is justified in believing that p if and only if S believes that p on a basis that properly probabilifies S’s belief that p” (Steup 2005). Most epistemologists seem to agree that DJ is not suitable for their purposes, at least in part because we have come to understand (post-Hume) that beliefs are not the sort of things over which we have much voluntary control, a high degree of which is required by a deontological approach to justification. Of course, much is packed in the concept of “properly probabilified,” but the point is that assessments of probabilities are more conducive to epistemically valid justification than deontological approaches (which tend to be more suitable — naturally — for moral, or even prudential, situations).

A second way to approach the issue of justification is from the point of view of its sources. In this case the two major positions are evidentialism (Conee and Feldman 1985) and the already mentioned reliabilism (Greco 1999). According to the first, a belief is justified if there is evidence in its favor, where the sources of evidence may be varied — including but not limited to perception, memory, introspection, intuition, etc. Following the latter, evidence is necessary but not sufficient, and it also has to be gathered by reliable means, which is more restrictive then the previous view. Again, a reliable source is then defined as one that “properly probabilifies” a given belief.

There is a third area of conceptual space that allows us to discuss justification, dealing with whether the latter is internal or external in nature (Kornblith 2001). Internalism (Steup 1999) takes it to be the case that whatever justifies a given belief boils down to a particular mental state we are in; this means, incidentally, that evidentialists tend to be internalists, because our evidence for one belief or another is always assessed by introspection of our own mental states. Fine, say the externalists, but the reliability of such evidence is not an internal (or purely internal) matter, which means that reliabilists tend simultaneously to be externalists. [33] The difference between the two positions is perhaps best fleshed out in cases in which someone has good reasons to accept a belief that is, as a matter of fact, false, as a result of radical deception. Consider, in the typical example, a brain in a vat who thinks he has hands (while he, obviously, doesn’t). In that case, the belief is justified from an internalist/evidentialist perspective (the mental states that form the basis for the belief are accessible), but not from an externalist/reliabilist point of view (since those mental states are, as it turns out, an unreliable source of belief).

We can also go back to the idea of knowledge itself and talk not about its most proper conceptualization, but its structure. Here the two main contenders in contemporary epistemology are foundationalism and coherentism. The first approach (DePaul 2001) — as the name implies — thinks of knowledge as structured like a building, with foundations upon which further knowledge is accumulated. Which implies that some beliefs are doxastically basic, i.e. they do not require any additional justification. It is, however, surprisingly difficult to find unchallenged examples of basic beliefs (give it a try, just as a mind stretching exercise). One proposal often advanced in this context is something along the lines of “It seems to me that the table is round,” which at least some foundationalists would argue is an example of a properly basic belief that cannot be successfully challenged — even if it turned out that the table is, in fact, oval. The problem is that, even if we agree that cases like the above do represent properly basic beliefs, they don’t get us very far unless we can extend the property of basicality to stronger statements, such as: “the table is round.” But the latter belief can be challenged on epistemic grounds, so one has to make a further move, invoking perceptual experience as evidence of both beliefs. Which in turn raises the thorny issue of why we should take perceptual experience to be a proper source of justification of some basic beliefs, given that we know it is not always reliable. [34] If we can get past these issues, foundationalists then can keep building their edifice of knowledge by deploying non-deductive methods, since to require further growth of knowledge by deductive approaches only would be too demanding — as Descartes quickly found out after engaging in his famous Cogito exercise (Descartes 1637/2000).

The second approach mentioned above is coherentism (BonJour 1999), according to which knowledge is structured more like a web (whiff-o-Quine, Chapter 3) than like a vertical structure with foundations. This means that there is no such thing as properly basic beliefs, as the strength of any given belief depends on its connections to the rest of the web (as well as on the strength of the other strands in the web). A major tool in the coherentist epistemic arsenal is the idea of inference to the best explanation (Lipton 2004). Consider again my belief that the table is round. Is it justified? Well, I could be hallucinating, I could be a brain in a vat, etc.. But, most likely my senses are working properly for a human being, I find myself under decent conditions of illuminations, not too far from the table, etc.. All of which allows me to inferentially converge on what appears to be the best explanation for what I see: the table really is round! Of course, the Cartesians amongst us (are there any left?), might object: couldn’t you being deceived by an evil demon (or, in more modern parlance, couldn’t you be in the Matrix)? Sure, I could, but — given what we think we know about how the world works (i.e., given our web of knowledge!) — that’s just not the best explanation available for my belief that the table is round, although it surely is a logically possible one.

Just like in any other area of philosophical conceptual space there are arguments pro and con both foundationalism and coherentism. Foundationalists, for instance, often deploy a regress argument: without foundation, one is forced to keep looking for justifications for one’s beliefs, and that search can only lead to an infinite regress or to a loop, neither of which are particularly satisfying prospects. However, not all circularity is bad (philosophers often make a distinction between circularity and vicious circularity). After all, one could argue that all deductive knowledge (i.e., great parts of logic and mathematics) is circular, and yet it is hardly to be dismissed on such grounds. Foundationalists can also buttress their position by attacking coherentism from a different angle: a system of beliefs could be entirely coherent and yet make no contact with reality. A well thought out fictional story, for instance, would fit the bill. But here the coherentist has a pretty straightforward response, I think: the web of belief that structures our knowledge of the world includes perceptual experience, and thereby does make contact with empirical reality. Foundationalists better accept this response, because if they retreat to the much more demanding position that knowledge needs logical (as opposed to empirical) guarantees, that would have to apply also to any properly basic (foundational) belief. That would result in a Pyrrhic victory. [35] Conversely, coherentists can counterattack against foundationalists by asking why (fallible) perceptual experience should be considered as justifying properly basic beliefs. And so on with successive refinements and counter-refinements of each position.

All this said and done, one can simply not leave even such a brief discussion of epistemology without posing the obvious question: if there has been progress in the study of epistemology, does this imply that we then have also made progress against skepticism (DeRose and Warfield 1999)? Skepticism has a long and venerable (some would say irritating) history in philosophy, dating back to the pre-Socratics. Plenty of valiant attempts have been made to overcome it. A modern version of the skeptic argument uses — again — the metaphor of the brain in the vat (BIV), and is therefore referred to by Steup (2005), from which the following discussion is adapted, as the BIV argument. It goes something like this:

(1) I don’t know that I’m not a BIV.

(2) If I don’t know that I’m not a BIV, then I don’t know that I have hands.

Therefore:

(3) I don’t know that I have hands.

This is a valid argument, so any viable response needs to challenge one of its premises — that is, challenge its soundness. Before proceeding, though, we must note (as Steup does) that premise (2) is tightly linked to (indeed, it is the negative version of) the so-called Closure Principle: “If I know that p, and I know that p entails q, then I know that q” — a principle that is definitely prima facie eminently reasonable. The application to our case looks like this: If I know that I have hands, and I know that having hands entails not being a BIV, then I know that I’m not a BIV. But — says the skeptics — the consequent of this “BIV closure” is false, hence its antecedent must be false too: you just don’t know whether you are a BIV or not!

There are several responses to the skeptic’s so-called “closure denial.” Steup examines a whopping five of them (concept map, anyone?): relevant alternatives, the Moorean response, the contextualist response, the ambiguity response, and what one might call the knowledge-that response. Let’s take a look.

A first attack against the BIV argument — a first peak in the relevant conceptual space — is to claim that being a BIV is not a relevant alternative to having hands; a relevant alternative would be, for instance, having had one’s hand amputated to overcome the effects of disease or accident. This sounds promising, but the skeptic can very well demand a principled account of what does and does not count as a relevant alternative. Perhaps relevance logic (Chapter 5) could help here.

Second attack/peak: G.E. Moore’s (1959) (in)famous response. This is essentially an argument from plausibility: the BIV goes through if and only if its premises are more plausible than its conclusions. Which Moore famously denied by raising one of his hands and declaring “here is one hand.” But why, asks (reasonably, if irritatingly) the skeptic? To make a long story short, Moore’s counter to the BIV argument essentially reduces to simply asserting knowledge that one is not a BIV. Which pretty much begs the question against the skeptic. [36]

Third branch in anti-skeptic conceptual space: the contextualist response. The basic intuition here is that what we mean by “know” (as in “I know that I have hands,” or “I don’t know that I’m not a BIV”) varies with the context, in the sense that the standards of evidence for claiming knowledge depend on the circumstances. This leads contextualists to distinguish between “low” and “high” standards situations. Most discussions of having or not having hands are low standards situations, where the hypothesis of a BIV does not need to be considered. It is only in high standards situations that the skeptical hypothesis becomes salient, and in those cases we truly do not know whether we have hands (because we do not know whether we are BIVs). This actually sounds most plausible to me (pretty high peak on the landscape?), though I would also like to see a principled account of what distinguishes low and high standard situations (unless the latter are, rather ad hoc, limited only to the skeptical scenario). Perhaps things are a bit more complicated, and there actually is a continuum of standards, and therefore a continuum of meanings of the word “know”? [37]

Fourth: the ambiguity response. Here the strategy is to ask whether the skeptic, when he uses the word “know,” is referring to fallible or infallible knowledge. (This is actually rather similar to the contextualist response, though the argument takes off from a slightly different perspective, and I think is a bit more subtle and satisfying.) Once we make this distinction, it turns out that there are three versions of the BIV argument: the “mixed” one (“know” refers to infallible knowledge of the premises but to fallible knowledge of the conclusion), “high standards” (infallible knowledge is implied in both premises and conclusion), and “low standards” (fallible knowledge assumed in both instances). Once this unpacking is done, we have to agree that the mixed version is actually an instance of invalid reasoning, since it is based on an equivocation; the high-standards version is indeed sound, but pretty uninteresting (okay, we don’t have infallible knowledge concerning our hands, so what?); and the low-standards version is interesting but unsound (because we would have to admit to the bizarre situation of not having even fallible knowledge of our hands!).

Finally: the knowledge-that response, which is a type of evidentialist approach. The idea is to point out to the skeptic that the BIV argument is based on a number of highly questionable unstated premises, such as that it is possible to build a BIV, and that someone has actually developed the technology to do so, for instance. But we can deny these premises on grounds of implausibility, just like we would deny, say, the claim that someone has traveled through time via a wormhole on the ground that we don’t have sufficient reasons to entertain the notions that time travel is possible and that someone has been able to implement it technologically. Yes, the skeptics can deny the analogy, but now the burden of proof seems to have shifted to the skeptic, who needs to explain why this is indeed a disanalogy.

Hopefully the above has allowed us to develop at least a general sense of the epistemological landscape and of how people have been exploring and refining it. It is now time to examine another area of philosophical inquiry which, in my mind, clearly makes progress.

Philosophy of science: forms of realism and antirealism

I’m a philosopher of science, and therefore better acquainted with that subfield than with anything else in philosophy. And it is clear to me that philosophy of science has also made quite a bit of progress from its inception (the approximate time of which may reasonably be pegged onto the famous debate on the nature of induction between John Stuart Mill and William Whewell, but which could be traced further back at the least to Bacon). In this section I will go over a specific example (among many, really) of progress in philosophy of science, the debate between realists and antirealists about scientific theories and unobservable entities (interested readers should also see the many useful references listed in the pertinent SEP entries: Monton and Mohler 2008; Ladyman 2009; Chakravartty 2011).

To begin with, let us be clear about what sort of debate this is: it concerns what our best epistemic attitude should be toward scientific theories, as well as toward the “unobservable” entities posed by most of these theories, such as electrons, strings and so forth. The broad contrast is between realist and antirealist positions, though each one comes in a variety of flavors and nuances. Within the context of this discussion, “observable” means by way of normal human sensorial experience (as opposed to scientifically observable): stars and dinosaur bones are observable; electrons and galaxies are not, in this sense. While the distinction so drawn is obviously arbitrary, since it is defined by the sort of human sensorial access to the world, that is precisely the point: the realist-antirealist discussion is one that concerns human epistemic limits within the context of science, as well as the degree to which our ontology should be justified by our epistemology.

Scientific realism comes with a number of commitments: epistemically, it takes scientific theories to yield knowledge about the world — as opposed to a more limited instrumentalist interpretation of those theories, which at most grants that we can have knowledge of observables, but not of unobservables. Metaphysically, for a scientific realist the world exists independently of human minds, a stance which is of course open to the Kantian objection that we do not have access to the world-in-itself, only to decidedly not mind-independent experiences. Semantically, scientific theories are to be taken at face value for the realist, as statements about the way the world is — as opposed to, again, instrumentally (i.e., they just work, in a pragmatic sense). Of course realists do typically admit that most scientific theories are, strictly speaking, false, which is why they often appeal to the notion of “truth-likeness,” rather than truth (see Chapter 4). As a result of this, realists tend to be fallibilists about scientific knowledge but nonetheless maintain that science makes progress by getting incrementally — though not necessarily linearly, or even always monotonically — closer to a true description of the world.

There are at the least three major varieties of realism, which are committed to stronger or weaker versions of the above. Entity realism holds that we have good reasons to be realists about any entity described by a scientific theory of which we have successful causal knowledge (e.g., black holes in cosmology); explanationism is the idea that we should be committed to realism with respect to the “best,” most indispensable, parts of scientific theories (e.g., quarks in fundamental physics); and structural realism is the position that we should be realist not about the entities invoked by scientific theories, but about the (mathematical) structure of those theories (e.g., treating the equations of Newtonian mechanics as a limit case of those from Special Relativity).

There are a number of arguments in favor of and against scientific realism, and the field has made progress precisely insofar these arguments have been presented, criticized, modified, further criticized, refined, and so forth, the by now familiar exploration by move and counter-move of philosophy’s conceptual spaces. Briefly, there are three major reasons typically deployed in favor of scientific realism, the best known of which is Putnam’s (1975, 73) “no miracles” argument: “[realism] is the only philosophy that doesn’t make the success of science a miracle.” To this, van Fraassen (1980) — a major critic of realism — responded that a different way of thinking about the issue is to consider good scientific theories as the conceptual equivalents of successful living organisms: adapted to their environment and therefore effective. That, in turn, raises the issue of what, exactly, accounts for the adaptness of a scientific theory, not an easy issue to address, given that we still lack a satisfying explanation of cultural evolution couched in selective terms (though plenty of people have been working on it). Another objection raised against the no miracles argument is constructed on a version of the base rate fallacy: we just don’t know what the baseline expectation for successful scientific theories is (i.e., we do not have an independent control against which to make assertions of success or failure), so on what grounds are we surprised by the effectiveness of science? I confess that I find this objection formally intriguing, but ultimately bizarre, unless one wishes to deny the truly astounding degree to which science has made progress compared to any other way that human beings have devised to learn things about the natural world.

The second standard argument in favor of realism is corroboration, the idea that if different means of empirical detection, or different theoretical approaches, converge on the same conclusions then we have good reasons to be realists about those conclusions, a meta- theoretical version of Whewell’s (1847) famous consilience of induction. For instance, Ladyman and Ross (2009) have argued that there are several theoretical invariants in fundamental physics, regardless of which of a number of currently competing theories about the basic structure of reality turns out to be true. It seems sensible, therefore, to suggest that those theoretical invariants will survive independently of which of the competing theories will eventually be settled on by fundamental physicists (this is a type of structural realism).

Finally, we have selective optimism, the suggestion that we can retain entities or theoretical structures from previous theories, if they keep playing a successful role in new theories, which in turn gives us reasons to be realists about those entities or structures. In the case of entities, Ladyman (2009) suggests that this nicely dovetails with the kind of theories of reference proposed by Putnam (1975) and Kripke (1980), which maintain that one may retain successful reference to certain entities (e.g., electrons) even in spite of substantial background theoretical changes, leading to a certain stability of epistemic commitments even in the face of theory change.

On the other side of the debate, there are well articulated (and just as carefully criticized) arguments against scientific realism. Perhaps the best known is the problem posed by the underdetermination of theory by data, which is closely related to the Duhem-Quine theses (Chapter 2). The idea is that there are always, in principle, many different theories that are equally compatible with the data, or — equivalently — that the available data is not enough to determine the truth of a theory and the falsity of closely related theoretical variants. The problem with this objection is that it is actually difficult to find historical examples of rampant underdetermination, or of an underdetermination that was not soon resolved. Then again, perhaps the best current example of massive underdetermination of theory by the data is string/M-theory in fundamental physics (Woit 2006; Smolin 2007; Baggott 2013), with its “landscape” of 10^500 (give or take) possible versions and essentially no empirical evidence to even tell us whether the broad outline of the story is correct.

A second standard objection to scientific realism is rooted in skepticism concerning the idea of the above mentioned inference to the best explanation (IBE), which can be articulated on two levels. First, there is criticism of the very concept of IBE, based on the difficulty to make explicit what criteria are to be deployed in order to determine that a given explanation is, indeed, “the best.” Should we use simplicity? Elegance? A combination of these, and what else? The matter is actually not at all trivial, though my sense is that most philosophers do think that IBE is a defensible type of inductive inference. Second, van Fraassen (1989) noted that at any given point in time in the history of science we may just have a “best of a bad lot” situation, so that even if we had a principled way to make an inference to the “best” (available) explanation, we would have no reassurance that such explanation was even in the ballpark of the true one.

Then we have the problem (for realists) posed by the so-called pessimistic meta-induction: Laudan (1981b) pointed out that the history of science provides us with a number of examples of theories that were thought to be correct and were eventually rejected. Thus, by standard inductive generalization one would be justified in concluding that current theories will also, eventually, turn out to be false. If there is no principled way to address this, then an epistemically modest attitude toward scientific theorizing — such as antirealism — seems warranted. The pessimistic meta-induction can be countered by deploying the notion of truth-likeness, the idea that we are getting incrementally closer to the truth in a way that can be argued without falling into question begging, and which I have already discussed in Chapter 4. Needless to say, antirealists have also criticized the very notion of truth-likeness.

So much for the basic version of scientific realism and its main flavors. Let me turn now to a symmetric treatment of the major alternative proposal, van Fraassen’s constructive empiricism. The opening salvo for a renewed attack on scientific realism was his The Scientific Image (1980, 12), at the onset of which he unequivocally threw the gauntlet down: “Science aims to give us theories which are empirically adequate; and acceptance of a theory involves as belief only that it is empirically adequate.” It is this book that is usually credited with the rehabilitation of the very idea of scientific antirealism, after the demise of logical positivism (Stadler 2012).

Constructive empiricism has much in common with logical positivism, particularly the commitment to purge what are perceived as unnecessary metaphysical burdens from our view of science; however, van Fraassen’s position — unlike logical positivism — does not rely on the (in)famous verification principle, nor does it shy away from the idea that scientific discourse is necessarily theory-laden. The crucial notion is that of empirical adequacy, which van Fraassen characterizes in this manner: “a theory is empirically adequate exactly if what it says about the observable things and events in the world is true — exactly if it ‘saves the phenomena’” (1980, 12). But constructive empiricism advances a number of additional ancillary notions, a particularly important one being the distinction between observables and unobservables, where the line separating the two categories of facts or entities is understood as relative to human beings qua epistemic agents.

As in the case of scientific realism, over time several arguments have been put forth in favor of constructive empiricism, and naturally many such arguments mirror the ones we have seen above about realism. We do not therefore need to revisit the idea of underdetermination of theory by data, or the pessimistic meta-induction. Beyond those, a major point highlighted by van Fraassen is that his preferred criterion of empirical adequacy is epistemically more modest — so to speak — than claims of truth, while still making sense of science as an epistemically successful activity. Another major difference between constructive empiricism and scientific realism is the way these two frameworks approach the proper relation between theory and experiment: realists think that experiments teach us about observables as well as unobservables, while constructive empiricists think that experiments only teach us about the former.

Pragmatism is big among constructive empiricists. They, for instance, follow a pragmatic approach to theory choice: van Fraassen rather astutely observes that scientists themselves often deploy criteria for theory selection that are not strictly epistemic, but — in fact — pragmatic, for instance, when a theory is preferred over another on grounds of simplicity, elegance, etc. He also advances a pragmatic view of explanation, providing a long list of past scientific theories that had explanatory power and yet turned out not to be true (this is conceptually distinct from the point about the pessimistic meta-induction): e.g., Newton’s theory of gravitation explained the movements of the planets, and Bohr’s theory explained the spectrum emitted by hydrogen atoms. It seems uncontroversial that scientific explanations do include a pragmatic component, but — adds the constructive empiricist — how can the scientific realist insist that they are good explanations because they are true statements about the world, given examples such as these and a number of others that can easily be gleaned from the history of science?

Indeed, van Fraassen’s pragmatism even extends to the very idea of laws of nature, which he regards as unnecessary metaphysical commitments, in explanatory terms, to which nonetheless the scientific realist seems wedded. Constructive empiricists point out that natural laws are actually only true on a ceteris paribus clause (a point famously also made by Nancy Cartwright: 1983), that is, they depend crucially on counterfactuals that are — strictly speaking — empirically inaccessible. Both the emphasis on empirical adequacy and the frontal assault on the sacred cow of natural laws is part and parcel of one of the major points in favor of constructive empiricism, according to its supporters: a philosophical program that puts a stop to “inflationary metaphysics.” As van Fraassen (1980, 69) clearly explains: “the assertion of empirical adequacy is a great deal weaker than the assertion of truth, and the restraint to acceptance delivers us from metaphysics.”

The idea is that the constructive empiricist can drop concepts such as those of laws of nature, natural kinds and the like, without any apparent loss in explanatory adequacy.

As in the case of scientific realism, there are a series of moves in conceptual space that various authors have made to dispute constructive empiricism — with the full ensemble of these moves and countermoves representing another instance of what I call progress in philosophy. We have already encountered some of these maneuvers, beginning with Hilary Putnam’s no-miracles argument, and with the scientific realist’s invocation of inference to the best explanation.

A less successful charge against constructive empiricism was led by Paul Churchland (1985), and it fundamentally hinged on the arbitrariness of the observable / unobservable divide drawn by van Fraassen. While prima facie reasonable, Churchland’s objection actually misses van Fraassen’s point: as explained above, the latter was not attempting to draw a hard metaphysical line between observable and unobservable, but simply making the more mundane empiricist observation that scientific knowledge is human knowledge, and therefore bounded by the limits of humans qua epistemic agents, including the by no means arcane fact that we can observe certain things and not others.

Be that as it may, a recent survey of philosophers’ positions (Bourget and Chalmers 2013) clearly gives realism the upper hand over anti-realism (75% vs 12%, give or take — see next Chapter for more details), though the survey itself does not discriminate among types of realism and anti-realism. One of the factors contributing to this disparity may be the next big leap in the exploration of the realism-antirealism conceptual space, to which I now turn: structural realism (Ladyman 2009), a conception first introduced by John Worrall in 1989, a few years after van Fraassen’s book.

Again recall that one of the most convincing grounds in favor of realism is Putnam’s no- miracles argument, and one of the strongest rebuttals by antirealists relies on some version of the pessimistic meta-induction, or at the least on the observation that major scientific theories of the past have been abandoned (something often referred to as “radical theory change”). It was therefore perhaps inevitable that the following major counter-move by realists is a novel type of challenge to the idea of radical theory change. Here is how Worrall (1989, 117) himself put it, in the case of a specific historical instance: “There was an important element of continuity in the shift from Fresnel to Maxwell — and this was much more than a simple question of carrying over the successful empirical content into the new theory. At the same time it was rather less than a carrying over of the full theoretical content or full theoretical mechanisms (even in ‘approximate’ form) ... There was continuity or accumulation in the shift, but the continuity is one of form or structure, not of content.” That is, the commitment by the realist should be to the mathematical or structural content of scientific theories — what, allegedly, gets conserved across theory change — rather than to specific unobservable entities or descriptions of those entities.

From a historical perspective, there are indeed a number of apparent cases of successful structural transition between scientific theories, besides Fresnel => Maxwell. For instance, Saunders (1993) has argued that there are surprising structural similarities between Ptolemaic and Copernican astronomy, as counterintuitive as that may seem. More convincingly, perhaps, Bohr famously argued that classical models in physics are a limit case of quantum mechanical ones, and the same is true of the relationship between classical mechanics and Special Relativity.

It is important to distinguish between two major varieties of structural realism, epistemic and ontic, each representing — in the model of progress in philosophy that we are exploring — a distinct local peak in the conceptual mountain range that defines the realism-antirealism debate. In the case of epistemic structural realism, the idea is that one is justified in being a realist about the relations between unobservables, while remaining agnostic as to their ontological status. Intellectual forerunners of this approach date back at the least to the beginning of the 20th century (e.g., Poincaré), and can be read according to a Kantian key: science gives us access to the structure of the noumenal world, but not to its substance. More recently, Maxwell (1972) has defended a modern interpretation of epistemic structural realism deploying the concept of Ramsey sentences (Papineau 2010; Frigg and Votsis 2011) and turning it into a semantic theory. However, Ladyman (1998) has argued that this doesn’t actually constitute much of an improvement over standard structural realism, and that a stronger, metaphysical (rather than just epistemological) move is necessary.

Which brings us to the ontic approach. As Worrall phrased it (1989, 57): “[O]ur science comes closest to comprehending ‘the real,’ not in its account of ‘substances’ and their kinds, but in its account of the ‘forms’ which phenomena ‘imitate’ (for ‘forms’ read ‘theoretical structures,’ for ‘imitate,’ ‘are represented by’).” The focus, in other words, is on the structure of the relations among things, not on the things themselves — hence the title of Ladyman and Ross’(2009) book, Every Thing Must Go. Indeed, ontic structural realism can be seen as a “naturalized metaphysics” based on the most current accounts of the fundamental nature of the world provided by physical theories where, because of phenomena such as quantum non-locality and entanglement, the deeper one digs the less one finds anything like physical objects at the bottom of it all.

There are, predictably, a number of objections that have been moved to ontic structural realism, a fundamental one being that it endorses a strange metaphysics where there are relations without corresponding relata, which strikes many commentators as being this (visualize a very very short distance between your index finger and thumb) close to absurdity. I do not wish to get into the details of this sort of discussion here, though the various criticisms and counter-criticism of ontic structural realism represent a micro- cosmic version of my general thesis about movement in philosophical conceptual space. Ladyman (2009) lists and discusses seven different ways available to supporters of ontic structural realism to respond to the relations-relata problem, ranging from biting the bullet and going Platonic, so to speak, to the idea that individual objects do not have intrinsic natures after all, to a rejection of Humean-type supervenience, just to mention a few. Regardless, and as I’ve stated above, a major point in favor of ontic structural realism is that it is consistent with — indeed it is partly inspired by — the view of reality that originates from current fundamental physics. In particular, physicists nowadays think in terms of fields, rather than particles, since particles, in a quantum mechanical sense, don’t really exist as individual entities and are better thought of as field attributes of space-time points, which sounds a lot like there are no “things” or relata, just relations.

Irrespective of the debate about relations sans relata, there are several other objections to ontic structural realism: without going too deep (see review by Ladyman 2009), Chakravartty (2004) is among those that argue that sometimes structure too is lost during theory change, resulting in so-called Kuhn-losses (Post 1971, Chapter 4). Another issue is that ontic structural realism essentially turns metaphysics into epistemology (which may or may not be a good thing in and of itself, depending on one’s philosophical leanings), because it defers too much to the results of the natural sciences (especially, or, rather, pretty much exclusively, fundamental physics). And the proper relationship between metaphysics and epistemology is, naturally, a whole separate area for discussion (Chalmers et al. 2009; Ross et al. 2013). Moreover, some critics (e.g., Chakravartty 2003) argue that ontic structural realism cannot account for causality, which notoriously plays little or no role in fundamental physics, and yet is crucial in every other science. For supporters like Ladyman causality is a concept pragmatically deployed by the “special” sciences (i.e., everything but fundamental physics), yet not ontologically fundamental.

A more serious objection, I think, is that even modern physics still lacks a way to “recover” macroscopic individuality from quantum non-locality (after all you and I are individuals in a rather strong sense of the term, unlike tangled electrons). Without this account, both fundamental physics and ontic structural realism look significantly limited. Related to this is the even broader point that structural realism essentially applies only to (again, fundamental) physics. There has been little or no effort to unpack the notion of theoretical structural conservatism in other areas of physics, let alone in any of the special sciences, for instance evolutionary biology. The fact that often enough theories in these other sciences don’t look particularly mathematical may be imputed to the relatively early stages of developments of those disciplines, but it may also represent a core limitation of a physics-centric way of looking at science as a whole. Finally, and this is to me a fascinating metaphysical point in itself, ontic structural realism basically collapses the distinction between the mathematical and the physical. Some mathematical physicists, like Max Tegmark (2014) have boldly gone down that route, talking about an essentially mathematical universe. As much as this sort of stuff is fun to think about, it does seem at the least problematic to make sense of the notion that mathematical structures are “real” in an even more fundamental way than physical entities themselves. And so the exploration of the pertinent conceptual landscape continues.

Ethics: the utilitarian-consequentialist landscape

It should be clear at this point that we could multiply the examples in this chapter by orders of magnitude, and cover — I suspect — most areas of philosophical scholarship. Instead, let me simply add one more class of examples, from ethics, focusing in particular on utilitarianism and the broader class of ethical theories to which it belongs, consequentialism. [38] The history of utilitarianism is yet another good example of progress in philosophy, with specific regard to the subfield of moral philosophy — and I say this as someone who is not particularly sympathetic to utilitarianism. The approach is characterized by the idea that what matters in ethics are the consequences of actions (hence its tight connection with the broader framework of consequentialism). The idea can be found in embryonic forms even earlier than the classic contributions by Jeremy Bentham and John Stuart Mill. For instance, Driver (2009) begins her survey with the theologically inclined 18th century British moralists, such as Richard Cumberland and John Gay, who linked the idea that promoting human happiness is the goal of ethics to the notion that God wants humans to be happy. This coincidence of our own desire for happiness and God’s plan for our happiness, however, provides a picture of utilitarianism that is too obviously and uncomfortably rooted in theology, and moreover where it is not at all clear what (philosophical) work God’s will actually does for the utilitarian.

The decisive move away from theological groundings and into natural philosophy was the result of the writings of people like Shaftesbury, Francis Hutcheson and David Hume. Shaftesbury proposed that we have an innate sense of moral judgment, although Hume did not interpret this in a realist sense (e.g., he did not think that moral right and wrong are objective features of the world, independent of human judgment). One can think of Shaftesbury as a “proto” utilitarian, since sometimes it is difficult to distinguish utilitarian from egoistic arguments in his writings, as argued by Driver (2009). The move to a more clearly utilitarian position is already found in Hutcheson’s An Inquiry Concerning Moral Good and Evil (1738), where he wrote: “so that that action is best, which procures the greatest happiness for the greatest numbers; and that worst, which, in like manner, occasions misery” (R, 283-4). Even in Hutcheson, though, we still don’t see a completely formed utilitarian approach to ethics, as he mixes in foreign elements, for instance when he argues that the dignity or “moral importance” of certain individuals may outweigh simple numbers of people affected by a given moral judgment.

Following Driver’s capsule history, proto-utilitarians were succeeded by the major modern founders of this way of looking at ethics: Jeremy Bentham and John Stuart Mill. Interestingly — and although much discussion and progress on utilitarianism has focused on Mill — the contrast between he and Bentham also highlights the difference between two branches in conceptual space: egoistic utilitarianism (Bentham) and so-called altruistic utilitarianism (Mill).

Bentham was influenced by both Thomas Hobbes and David Hume. He got his theory of psychological egoism from the former and the idea of social utility from the latter, but the two were otherwise incompatible: it is hard to imagine an egoist who agrees to the notion of social utility above and beyond what is useful for himself. Hobbes was aware of this problem in his approach, though his attempts to deal with it were less than satisfactory. For instance, he thought that a reconciliation between the two perspectives could arrive by way of empirical investigation, if the latter showed a congruence between personal and social welfare. But that is no principled way to resolve the issue, as one still has to decide which branch of the fork to take in case the empirical evidence is not congruent. Probably as a result of this sort of difficulties, Bentham simply decided to abandon his commitment to psychological egoism and a fully Hobbesian view of human nature in favor of a more moderate, more Humean, take. Hume, in turn, was no utilitarian, as he thought that character was the salient focus when it comes to ethical judgment. But Hume also wrote about utility as the measure of virtue, and that is what Bentham adopted from him, particularly because Bentham was interested in distinguishing between good and bad legislation (respectively characterized by positive and negative consequences in terms of social utility).

Driver (2009) highlights Bentham’s discussion of homosexuality, in which he explains that having an antipathy for an act is simply not sufficient to justify legislation against it. The quote is remarkably modern, reminding me of recent social psychology results like those discussed by Jonathan Haidt (2012) to the effect that people have a tendency to confuse a sense of disgust for a well founded moral judgment: “The circumstances from which this antipathy may have taken its rise may be worth enquiring to ... One is the physical antipathy to the offense ... The act is to the highest degree odious and disgusting, that is, not to the man who does it, for he does it only because it gives him pleasure, but to one who thinks of it. Be it so, but what is that to him?” (Bentham 1978, 4, 94). The bottom line, for Bentham, is that actions are not intrinsically good or bad, but only good or bad in proportion to their consequences in terms of social utility. Not only this disqualifies obviously suspect candidates as sources of moral evaluation, like whether an act is natural or not; it also means that values such as personal autonomy and liberty are only instrumentally, not fundamentally, good (i.e., they can be overridden, if need be).

The first major move away from Bentham’s starting point in exploring the utilitarian landscape was Mill’s rejection of the idea that differences between pleasures are only quantitative, not qualitative. That position had opened Bentham to a number of objections, including that sentient animals would therefore acquire the same moral status as humans, and the observation that Bentham had no way to discriminate between what Mill eventually referred to as “lower” and “higher” pleasures: drinking a beer while watching the World Cup should, for Bentham, be the same as listening to Beethoven. [39] Mill’s famous defense of the distinction between higher and lower pleasures is itself open to criticism, hinging as it does on the problematic idea that people who are capable of enjoying both types of pleasure are best suited to make judgments about it. As he famously put it: “It is better to be a human being dissatisfied than a pig satisfied; better to be Socrates dissatisfied than a fool satisfied. And if the fool, or the pig, are of a different opinion, it is because they only know their own side of the question” (1861, ch. 2).

As noted above, though, the major difference between Mill and Bentham lies in their respective views of human nature, where Mill’s is more positive, including the idea that a sense of justice, for instance, is a natural human impulse, which we can then refine and expand by way of reason — in this Mill was very much aligned with Hume (Gill 2000), and arguably influenced even by the ancient Stoics (Inwood 2003). However, Bentham’s and Mill’s ways of looking at utilitarianism also had quite a bit in common. For instance neither of them was intrinsically opposed to the idea of rights, although for a utilitarian any talk of rights has to be couched in terms of utility, as there is no such thing as a natural right (a concept that Bentham famously dismissed as “nonsense on stilts”).

The next majors leap in utilitarian conceptual landscape was made by Henry Sidgwick, with his The Methods of Ethics (1874). Sidgwick noticed a major ambiguity at the heart of early utilitarian philosophy: “if we foresee as possible that an increase in numbers will be accompanied by a decrease in average happiness or vice versa, a point arises which has not only never been formally noticed, but which seems to have been substantially overlooked by many Utilitarians. For if we take Utilitarianism to prescribe, as the ultimate end of action, happiness on the whole, and not any individual’s happiness, unless considered as an element of the whole, it would follow that, if the additional population enjoy on the whole positive happiness, we ought to weigh the amount of happiness gained by the extra number against the amount lost by the remainder” (1874, 415). In other words, utilitarians need to distinguish between the average degree of happiness in the population and the sheer number of individuals enjoying that degree of happiness. If the goal is to increase happiness tout court, then this can be accomplished either by increasing population size while keeping average happiness constant (logistical issues aside, of course), or by keeping the population constant and increasing the average happiness of individuals. So the quantity that utilitarians really need to focus on is the product of population size and average happiness.

By the turn of the 20th century yet another refinement in conceptual space was made to basic utilitarian doctrines, chiefly by G.E. Moore. Like Mill before, he realized that Bentham’s original views did not discriminate between types of pleasures, some of which ought to be regarded as positively unethical. Bentham had no principled way of discounting the pleasure felt by sadists, for instance, as long as it somehow outweighs the pain they inflict on their victims. Moore then developed a pluralist (as opposed to a monist) doctrine of intrinsic value. The good cannot be reduced simply to pleasure, as it comes in a variety of forms. For Moore, beauty is also an intrinsic good, a position that led him to excuse on ethical grounds cases in which artists pursue their muse while at the same time abandoning their duties to their family (e.g., Gauguin), as long as the result of such tradeoff is more beauty in the world.

Moore’s (admittedly a bit vague) idea of the “organic unity” of value also helped utilitarians improve their framework by pre-empting a number of objections that had been raised in the meantime. The concept of organic unity is drawn from an analogy with the human body, where it makes little sense to talk about the value of individual organs, adding them up to get the total value of the whole body. Rather, one needs to take into account how the parts fit into the whole. Similarly, according to Moore, experiencing beauty has value in itself, and that value is augmented if the beautiful object actually exists. But the combination of these two elements is much more than the simple addition of the two parts, a position that allows Moore and fellow utilitarians to conclude that happiness based on knowledge is much better than happiness based on delusions. Again, notice the struggle to recover Mill’s intuition that not all pleasures are created equal, and to arrive at a rationally defensible view of why, exactly, that is the case.

Once we get firmly into the 20th century the history (and progress in conceptual space) of utilitarianism coincides with the broader history of consequentialism (Sinnott-Armstrong 2006). From this perspective, classic utilitarianism can be seen as a type of act consequentialism, where the focus is on the rightness of acts in terms of increasing the good (say, happiness), as their consequence. Modern consequentialism is also an improvement on classic utilitarianism because it parses out a number of positions more or less implicitly accepted by early utilitarians, positions that carry distinct implications for one’s general ethical framework. For example, there is a difference between actual and direct consequentialism — in the first case what matters are the actual consequences of a given action (not the foreseeable ones), while in the second case what counts are the consequences of the focal act itself (not one’s motives for carrying out the action). Or take the distinctions among maximizing, total and universal consequentialism, where the moral good of an action depends respectively on the best consequences, on their total net effect, or on their effect on all sentient beings. The issue is not that these (and other) utilitarian positions are necessarily contradictory, but that each needed to be unpacked and explored independently of the others, to arrive at a more fine grained picture of the consequentialist landscape as a whole.

One specific example of improvement on a thorny issue for early utilitarians is the problem posed by hedonism. [40] I have mentioned that Bentham could not discriminate between what most people would recognize as morally good pleasures and those of a sadist, and both Mill’s and Moore’s attempts to improve on the problem only went so far. Nozick (1974) took a further step forward with his experience machine thought experiment (famously re-imagined in the movie The Matrix). The idea is to consider a hypothetical machine that is capable of mimicking the feeling of real experiences in all respects, so that one could live as “happy” and “successful” a life as conceivable. Yet one would not be living a real life as commonly understood. Nozick’s contention was that it does not seem at all irrational for someone to refuse to be hooked to the experience machine, thus creating a significant problem for a purely hedonistic view of utilitarianism, necessitating its abandonment or radical rethinking. One way modern consequentialists (e.g., Chang 1997; Railton 2003) have attempted to tackle this issue is through the recognition of the incommensurability of certain moral values, and hence the in principle impossibility to resolve certain ethical dilemmas, which in turns leads to a (non-arbitrary) type of utilitarian pluralism.

Another standard problem for utilitarianism, suitable to illustrate how philosophers recognize and tackle issues, is of an epistemic nature: when we focus on the consequences of morally salient actions, are we considering actual or expected consequences? The obvious limitation plaguing classic utilitarianism — as was noted by Mill himself — is that it seems to require an epistemically prohibitive task, that of calculating all possible ramifications of a given action before arriving at a consequentialist judgment. One option here is to say that the utility principle is a criterion to decide what is right, but that it does not amount to a decision making algorithm. While this may make it sound like utilitarians cornered themselves into a self-refuting, or at the least, morally skeptical position, this is not necessarily the case. Consider an analogy with an engineer deploying the laws of physics to draw and then build a bridge. In order to accomplish the task, the engineer needs to know enough about the laws of physics and the properties of the materials she is about to use, but it would be unreasonable to pretend omniscience about all outcomes of all potential physical interactions, however rare, between the bridge and its surrounding environment — some of which interactions may actually cause the obviously unintended consequence of the collapse of the bridge. Similarly, the utilitarian can say that under most circumstances we have sufficient knowledge of human affairs to be able to predict the likely consequences of certain courses of action, and therefore to engage in the same sense of approximate, and certainly not perfect, calculation that the engineer engages in. We have good guiding principles (the laws of physics for the engineer, the utility principle for the moral person), but we face a given degree of uncertainty concerning the actual outcome.

Even so, the consequentialist is not home free yet, since a critic may make another move that manages to raise additional issues. If we shift our focus to the sort of consequences that can reasonably be contemplated by the limited epistemic means available to human beings, are we then talking about foreseen or foreseeable consequences? There is a distinction there, but it isn’t clear the extent to which it is sharp enough to be morally salient. Generally speaking the range of foreseeable consequences of a given action is broader — sometimes much broader — than the range of consequences actually foreseen by any given agent. Consider an analogy with chess playing: the gap between foreseen and foreseeable may be narrow in the case of a Grand Master, but huge in the case of a novice. The analogy, however, points toward the fact that — rather than being a problem for consequentialism per se — the distinction between foreseen and foreseeable consequences suggests that we as a society should engage in better ethical training of our citizens, just like better training is at least part of what makes the difference between a Grand Master (or even a half decent player) and a novice.

As I mentioned before, although Mill talked about rights, the concept poses significant and well known issues for consequentialists, as illustrated by the famous problem of the emergency room. The human body has five vital organs (brain, heart, kidneys, liver, and lungs). Imagine you are a doctor in an emergency room and you are brought four patients, respectively whose heart, kidneys, liver and lungs are all failing (there would be nothing you could do about a patient with a failing brain, so we won’t consider that situation). On utilitarian grounds, why would it not be acceptable for you to go outside, pluck a healthy person at random from the sidewalk, and extract four of his vital organs to distribute among your patients? Prima facie you are saving four lives and losing one, so the utility calculus is on your side. [41]

Utilitarians here have a number of options available as countermoves in logical space. The simplest one is to bite the bullet and acknowledge that it would, in fact, be right to cut up the innocent bystander in order to gain access to his vital organs. A rational defense of this position, while at the same time acknowledging that most people would recoil in horror from considering that course of action, is that the concocted example is extreme, and that our moral intuitions have evolved (biologically or culturally) to deal with common occurrences, not with diabolical thought experiments. Few utilitarians, however, have the stomach to go that route, thankfully. An alternative move is to agree that the doctor ought not to go around hunting for vital organs by drawing a distinction between killing and dying, where the first is morally worse than the second. The doctor would be killing an innocent person by engaging in his quest, while the four (also innocent) patients would die — but not be killed — by his inaction, forced upon him by the lack of acceptable alternatives. A third available move is to introduce the concept of the agent-relativity of moral judgment. The idea is that we can see things either from the point of view of a dispassionate observer or from that of the moral agent (here, the doctor), and the two don’t need to agree. In the specific case, the observer may determine that a world in which the doctor cuts up an innocent to extract his vital organs is better — utility-wise — than a world in which the doctor does not act and lets his patients die. But the doctor may justifiably say that he also has to take into account the consequences for him of whatever course of action, for instance the fact that he will have to live with the guilt of having killed a bystander if he goes through with the nasty business. The world would therefore be better or worse depending on which perspective, the observer’s or the agent’s, one is considering, without this implying a death blow — so to speak — to the whole idea of consequentialism.

One more significant branching in conceptual space for consequentialism is represented by the distinction between direct and indirect varieties of it, where a direct consequentialist thinks that the morality of X depends on the consequences of X, while an indirect consequentialist thinks that it depends on consequences of something removed from X. There are several sub-types of both positions. Considering indirect consequentialism, for instance, this can be about motives, rules, or virtues. Indirect rule consequentialism is probably one of the most common stances, holding that the moral salience of an act depends on the consequences of whatever rule from the implementation of which the act originated. At this point, though, if you suspect that at the least some types of indirect consequentialism begin to look less like consequentialism and more like one of its major opponents in the arena of ethical frameworks (i.e., rules consequentialism approaches deontology, while virtue consequentialism approximates virtue ethics) you might be onto something.

Yet another popular criticism of generalized utilitarianism is that it seems to be excessively ethically demanding of moral agents. Peter Singer’s (1997) famous drowning child thought experiment (as you might have noticed by now, many thought experiments concerned with utilitarianism tend toward the gruesome) makes the situation very clear. Singer invites us to consider seeing a child who is about to drown when we have the ability to save him. To do so, however, we would have to get into the water without delay, thus ruining our brand new Italian leather shoes. Clearly, I would hope, most people would say damn the shoes and save the child. But if so, points out Singer, why don’t we do the analogous thing all the time? We could easily forgo our next pair of shoes (or movie tickets, or dinner out, or whatever) and instead donate money that would save a child’s life on the other side of the planet. Indeed, Singer himself is famous for putting his money where his mouth is, so to speak, and donate a substantial portion of his income to charitable causes (Singer 2013). The problem is that, at least for most of us, this utilitarian demand seems excessive, confusing what is morally required with what may be morally desirable but optional. Can utilitarians somehow avoid the seemingly unavoidable requirement of their doctrine to expand far beyond what seems like a reasonable call of duty for the typical moral agent? If not, they would essentially be saying that most of what we do everyday is, in terms of utility, downright morally wrong — not exactly the best way to win sympathizers for your ethical framework.

Once again, several alternatives are available in conceptual space, and we have already encountered a number of the necessary tools to pursue them. One goes back to Mill himself, who argued that it may be too costly to punish people who do not agree to Singer-style demands posed upon them, in which case utility would be maximized by not imposing that kind of burden on moral agents. Or one may invoke agent-relative consequentialism, granting that the agent’s and a neutral observer’s perspective are sufficiently different to allow the agent a way out of the most stringent constraints. My favorite among the available offerings is something called satisficing consequentialism, which maintains that utility cannot always be maximized, so that it is morally sufficient to generate “enough” utility. This may sound like an easy way out for the consequentialist, but it actually has a parallel with the process of natural selection in evolutionary biology. A common misconception of natural selection is that it is an optimizing process, i.e. that it always increases the fitness of the organism to its maximum possible value. But both empirical research and theoretical modeling (e.g., Ward 1992) actually show that natural selection is rather a satisficing mechanism: it produces organisms whose degree of adaptation to their environment is “good enough” for their survival and reproduction. The reason for this is analogous to the one that motivates satisficing consequentialism: to go beyond good enough would be too costly, and in fact would end up not maximizing fitness after all.

The sort of examples we have briefly examined in this section could easily be multiplied endlessly, even branching into other ethical frameworks (e.g., evolution of and progress in virtue ethics, or deontology), as well as to entirely different areas of philosophical inquiry (metaphysics, aesthetics, philosophy of mind, and so forth). But I hope that the general point has been made sufficiently clearly. Even so, the reader may also suspect that some of this back-and-forth in conceptual space may, in the end, be rather pointless (I discussed this briefly in the Introduction, in the specific case of “Gettierology”). And some (maybe even a good amount) of it probably is. But let me explain and expand on this a bit, by way of concluding this chapter with a commentary on Dan Dennett’s (2014) distinction between chess and chmess, and why it pertains to the subject matter of this entire book.

But is it useful? On the difference between chess and chmess

“Philosophy is garbage, but the history of garbage is scholarship,” said Harvard philosopher Burton Dreben, as quoted by Dennett in chapter 76 of his often delightful and sometimes irritating Intuition Pumps and Other Tools for Thinking (2014). One could reasonably wonder why an illustrious philosopher approvingly quotes another illustrious philosopher who is trashing the very field that made them both famous and to which they dedicated their lives. But my anthropological observations as a relative newcomer (from science) into philosophy confirm that my colleagues have an uncanny tendency to constantly shoot themselves in the foot, and often even enjoy it (as we have seen in Chapter 1).

Be that as it may, Dreben’s comment does ring true, though it should be (slightly) modified to read: a lot of philosophy is garbage, but the history of garbage is scholarship. The fact is, however, that the very same thing can (and should) be said of scholarship in any field. Perhaps the case will not be controversial for certain particular areas of academic inquiry (which shall go duly unspecified), but I think the “a lot of garbage” summary judgment applies also to science itself, the current queen of the academy. Indeed, this was said as early as 1964 by John Platt, in a famous and controversial article published in Science magazine. Here is how he put it: “We speak piously of taking measurements and making small studies that will ‘add another brick to the temple of science.’ Most such bricks just lie around in the brickyard.”

I’ve done and read a significant amount of scholarship in both the natural sciences (biology) and philosophy (of science and related fields) (e.g., Pigliucci 2001; Pigliucci and Kaplan 2006) and I can attest that what Platt, Dreben and Dennett say is pretty much uncontroversially true. And moreover, that many people working in those fields recognize it as such, except of course when it comes to their own little bricks in the temple. How is this possible? Dennett explains it in terms of the difference between chess and chmess. I will assume that we are all familiar with the first game. The second one is Dennett’s own invention, and works exactly like chess, the only difference being that the King can move two, rather than one, squares in every direction. Needless to say, many people play (and care about) chess. Not so many are into chmess.

Dennett further explains that a lot of scholarship in philosophy is like trying to solve chess problems — which resonates exactly with what I have been trying to convince the reader of for a while now: philosophical inquiry is a search for logical truths that hold within a defined conceptual space of possibilities. As far as it goes, it’s not a bad analogy, except for the fact that quite a bit of philosophy is actually concerned with the sort of conceptual problems that matter in real life (think epistemology, ethics, political philosophy, and even philosophy of science, at its best), which means it also needs to be informed by the findings of both the natural and social sciences. Still, Dennett’s point is that trying to solve logical problems posed by chmess is just as difficult as trying to solve the very similar problems posed by chess, with the crucial difference that almost nobody gives a damn about the former. A lot of philosophers, he maintains, devote their careers to studying chmess, they are quite good at it, and they manage to convince a small number of like minded people that the pursuit is actually worth a lifetime of efforts. But they are mistaken, and they would realize it if they bothered to try two tests, also of Dennett’s own devising:

1) Can anyone outside of academic philosophy be bothered to care about what you think is important scholarship?

2) Can you manage to explain what you are doing to a bunch of bright (but, crucially, uninitiated — i.e., not yet indoctrinated) undergraduates? (For obvious reasons, your own colleagues and graduate students don’t count for the purposes of the test.)

I think Dennett is exactly right, but — again — I don’t think the tests in question should be carried out only by philosophers. Every academic ought to do it, as a matter of routine. I cannot begin to tell you about the countless number of research seminars in biology I have attended over decades, and about which the recurrent commentary in my own head (and, occasionally, with colleagues and students, after a glass of wine) was: “clever, but who cares?” Another quip quoted by Dennett, this one by Donald Hebb, comes to mind: “If it isn’t worth doing, it isn’t worth doing well.”

So, what, if anything, should be done with this state of affairs? This is a crucial question, which can be reformulated as: why should the public keep supporting universities (and, in the sciences, provide large research grants) to people who mostly, and perversely, insist in wasting (or at the least, underutilizing) their lives while figuring out the intricacies of chmess? Similarly, shouldn’t Deans, Provosts and university Presidents tell their faculty to stop squandering their brain power and get on with some project more germane to the public’s interest, or else? Francis Bacon might have agreed. He famously thought that the very point of human inquiry is not just knowledge broadly construed, but specifically knowledge that helps in human affairs. His famous motto was Ipsa scientia potestas est, knowledge is power. Power to control nature and to improve our lives, that is. In fact, even the famous Victorian debate on the nature of induction between John Stuart Mill and William Whewell (Snyder 2012), which pretty much began the modern field of philosophy of science, was actually a debate about the best way to gain knowledge that could be deployed for socially progressive change, to which both Mill and Whewell were passionately committed.

One answer to what to do about the problem is provided by Dennett himself in his essay referenced above: “let a thousand flowers bloom ... but just remember ... count on 995 of them to wilt.” Which essentially — and a bit more poetically — echoes Platt’s sentiment from half a century before. That seems right, and it is particularly easy to see in the case of basic (as opposed to applied, or targeted) scientific research, although it goes also for scholarship in philosophy, history, literary criticism or what have you. The whole thing is predicated on what amounts to a shotgun approach to knowledge: you let people metaphorically fire wherever they wish, and statistically speaking they’ll occasionally hit a worthy target. Crucially, there doesn’t seem to be a way, certainly not a centralized or hierarchically determinable way, to improve the efficacy of the target shooting. If we want knowledge about the world (or anything else), our best bet is to give smart and dedicated people pretty much free rein and a modest salary, then sit back and wait for the possible societal returns — which will fail to materialize more than 99% of the times.

So, yes, much of philosophical (and other) scholarship is indeed more like chmess than chess, and we may justifiably roll our eyes when we hear about it. But the difference between chmess and chess is not always clear, and it’s probably best left to the practitioners themselves and their communities to sort it out. The important point is that we do make progress in our understanding of whatever game we are playing as long as we allow smart and dedicated people to keep playing it.

7. Where Do We Go Next?

“Life can only be understood backwards; but it must be lived forwards.” (Søren Kierkegaard)

Philosophy has been declared dead by a number of people who have likely never read a single philosophy paper or technical book, and philosophers themselves have at times been the worst critics of their own field (Chapter 1). The discipline is vast, with a very long history marked by traditions so different from each other that one can reasonably question whether they can meaningfully be grouped under the same broad umbrella (Chapter 2). The field has seen internal revolutions as late as the middle and late part of the 20th century, with some philosophers going so far as claiming that major branches of their discipline ought to be handed over to the natural or social sciences (Chapter 3). Much of the criticism of philosophy, nowadays as in the time of Socrates, is that it doesn’t seem to go anywhere, it doesn’t make “progress.” Indeed, the reason the comparison with science arises so often is precisely because the latter is taken to be the standard of progressive fields of inquiry. And yet, even though it is certainly undeniable that science has made sometimes spectacular progress, we have also seen just how difficult it is to make precise sense of that observation, an eminently philosophical question if there ever was one (Chapter 4). Throughout the book I have advanced the thesis that philosophy does make progress, but that this ought to be understood in a manner significantly different from the way in which the concept applies to the sciences, and specifically in a fashion more akin — though again not exactly analogous — to the way in which mathematics and logic make progress (Chapter 5). I have suggested we think of philosophy as moving, and making progress, in a kind of (empirically informed) conceptual space, discovering and refining what Nicholas Rescher called aporetic clusters, which are themselves “evoked” — to use Lee Smolin’s terminology — by philosophers’ choices of assumptions and internally generated problems (Introduction). As a result, we should see philosophy as being in the business of proposing “accounts” (i.e., ways of understanding) and “frameworks” (i.e., ways of thinking) of whatever subject matter it applies itself to, as distinct from “theories” in the quasi-scientific sense of the term (Chapter 6).

In order to conclude our exploration of the nature and methods of philosophy, then, this chapter will look both at some new directions of which practicing philosophers ought to be aware (and even critical, when necessary), such as so-called experimental philosophy, as well as the heterogeneous movement known as “digital humanities.” We will also briefly re-examine with fresh eyes the classical toolbox that has made philosophical inquiry what it is, for good and for ill: thought experiments, intuitions, reflective equilibrium, and the like. Finally, we will discuss — quantitative data in hand! — what philosophers think about major issues within their own discipline, thus finding empirical support for the idea that philosophers are concerned with exploring multiple intellectual peaks in a vast conceptual space, where the very issue of finding “the” answer to a particular question will increasingly appear to be a misguided way of looking at things.

The Experimental Philosophy challenge

Most philosophers, and by now even members of the general public, are aware of a “movement” that has developed over the past several years and that is usually referred to as experimental philosophy, colloquially known as “XPhi.” I first encountered it at one of their early meetings many years ago, and as a (then) practicing scientist my initial reaction was very sympathetic. I thought: good, finally philosophers are getting their arse off the proverbial armchair and actually gather facts instead of just thinking about stuff. Now that I have been a practicing philosopher (firmly attached to my nice and comfortable armchair) for a while, I’ve become a bit more wary of some of the loudest claims made by XPhi supporters based on empirical investigations into what people think about a number of philosophical questions, as well as of the value of such findings for professional philosophers. I keep reminding myself that we already have a name for disciplines characterized by inquiry based on the collection of data about human opinions: they are called social sciences, and while they certainly ought to inform philosophers in what they do, they seem to me sufficiently distinct from philosophy that the two should not be confused.

Nonetheless, it would be unwise to reject XPhi without proper examination, especially at a time in which philosophy as a discipline is under attack for its assumed irrelevance and for not behaving like a science. I have had a number of conversations and email exchanges with Joshua Knobe, [42] arguably the most recognizable (and likable!) of the proponents of XPhi, and he tried his best to make me understand why he thinks his movement should be accorded full status as a sub-discipline of philosophy. [43] I cannot possibly do justice to the burgeoning literature (pro and con) XPhi, but a book on the nature and future of philosophy would simply be woefully lacking if it didn’t briefly engage with the issue. I begin, therefore, with a very clearly written survey of the methods and accomplishments of XPhi by Knobe et al. (2012; it is interesting to note that the paper was published in the Annual Review of Psychology).

Knobe and colleagues begin the paper by stating that “a guiding theme of the experimental philosophy movement is that it is not helpful to maintain a rigid separation between the disciplines of philosophy and psychology.” This, of course, is pure Quine (Chapter 3), and — as stated before — I doubt anyone can come up with a sensible objection to that general principle. The real questions concern: a) whether this move leaves sufficient autonomy to philosophy to maintain it as a distinct field of inquiry; and b) if so, what novelties or insights does the psychological approach provide into philosophical problems. Which is the very point of the review in question, a point articulated by its authors via a series of examples of philosophical issues to which they feel XPhi has contributed by means of experimental approaches. Let us therefore examine the four case studies proposed by Knobe et al. and see what we may reasonably make of them.

Case Study 1: Morality and concept application

XPhi researchers have explored how laypeople react to a number of standard hypothetical situations concerning moral judgment, such as the ones encapsulated by the following two standard scenarios:

(a) The vice president of a company went to the chairman of the board and said, “We are thinking of starting a new program. It will help us increase profits, and it will also help the environment.” The chairman of the board answered, “I don’t care at all about helping the environment. I just want to make as much profit as I can. Let’s start the new program.” They started the new program. Sure enough, the environment was helped. Did the chairman intentionally help the environment?

(b) The vice president of a company went to the chairman of the board and said, “We are thinking of starting a new program. It will help us increase profits, and it will also harm the environment.” The chairman of the board answered, “I don’t care at all about harming the environment. I just want to make as much profit as I can. Let’s start the new program.” They started the new program. Sure enough, the environment was harmed. Did the chairman intentionally harm the environment?

The authors found that people respond asymmetrically to these hypothetical scenarios, saying that the chairman unintentionally helped the environment in the first case, but intentionally harmed it in the second one. While these results are interesting in terms of understanding how people’s moral judgments are deployed, one can still sensibly ask what bearing do they have on the philosophical question of the moral status of the chairmen in the two examples. Presumably (I am speculating from my armchair here!), a trained moral philosopher will see that said chairman did, in fact, unintentionally help the environment in the first scenario (and thus gets no moral credit for his decision) while also understanding that the harm caused to the environment in the second case was intentional, but secondary (the primary motive wasn’t harming the environment, it was making a profit, but the chairman was warned of the environmental consequences of his actions). Of course we don’t know what most moral philosophers would say because the XPhi researchers didn’t carry out the proper experiment — which should have been done on philosophers, not members of the general public, assuming that the goal was to advance our understanding of ethics, not to run a survey of laypeople’s uninformed opinions. (Also notice that I gave reasons for my “intuitions” concerning the two cases. These reasons could in turn be subject to further scrutiny, and so on.)

Case study 2: Moral objectivism vs moral relativism

Here again, the empirical data gathered by the XPhi program is interesting, as it shows, for instance, that young and elderly people tend toward moral objectivism (the proposition that moral statements are objectively true or false), while people of intermediate age reason in more relativistic terms (the idea that moral statements are a reflection of local customs and habits). Again, however, this sort of evidence seems to be pretty much orthogonal to whether and how objectivism or relativism are philosophically defensible at the meta-ethical level.

XPhi researchers have also shown that “framing,” that is, how exactly a question is presented to respondents, makes a difference when people are asked to exercise a given moral judgment. For example, if a hypothetical scenario is presented in which two agents arrive at different moral judgments on a specific issue while belonging to the same culture, most respondents say that one of them must be wrong. However, if the two agents are postulated to belong to very different cultures, and yet also arrive at distinct judgments on the same issue, then most respondents say that both views may be correct. I would hope, however, that no serious (professional) ethicist would engage in that sort of shifting judgment, certainly not without a detailed analysis of what exactly the agents were disagreeing about and whether the disagreement is or is not amenable to reasonably different cultural stands.

Case Study 3: Free will

The experimental results concerning this old chestnut of metaphysics indicate that people tend to attribute moral responsibility to agents when a strong emotional response is elicited, even though they are told that such agents operate in an entirely deterministic universe. Again, however, how many moral philosophers, or metaphysicians, I wonder, would make that sort of naive mistake?

Knobe et al. claim that “the results shed light on why philosophical reflection and debate alone have not led to more universal agreement about the free will problem.” I don’t see how this follows from the results at all. The disagreement about free will among professional philosophers can be much better understood as deriving from the fact that the three major positions on the subject — deterministic incompatibilism, libertarian incompatibilism and compatibilism (see Griffith 2013 for a brief accessible survey; for a more in-depth survey see: O’Connor 2010) — occupy three peaks in conceptual space that are all defensible in the absence of crucial empirical evidence, though I would say that they are not all equally defensible, for instance because determinism increasingly seems the correct metaphysical view, thus excluding libertarian incompatibilism. This state of affairs is altogether different from the (confused) reasons why laypeople disagree and even contradict themselves on free will, a topic to which they do not typically devote a lot of time for reflection (well, actually that truly is an empirical question, I’m just guessing here).

Case Study 4: Phenomenal consciousness

Here XPhi researchers have explored what happens when people make the judgment that an object or potential agent does or does not possess the capacity for phenomenal consciousness as distinct from cognition. For instance, respondents tended to rate babies high on a scale of consciousness but low on cognition, while they rated gods inversely (i.e., high on cognition, low on consciousness). However, since we know nothing at all about gods, while we can actually do empirical research on children, it is hard to see why this counts as a genuine philosophic conundrum, as distinct from an interesting insight into human psychology.

Related research shows that people use different cues to arrive at an attribution of consciousness, especially behavior and embodiment. For instance, corporations and robots — both of which lack a biological body — tend to be regarded by most people as the kind of thing that does not have phenomenal consciousness. Again, though, I’m reasonably confident that a professional philosopher would never attribute consciousness to a corporation, while the issue for biological vs artificial bodies is very much one alive in both philosophy of mind and neuroscience. The crucial question, as far as we are concerned here, is whether the latter problem is actually informed by the (interesting, for sure) fact that people who know nothing about philosophy of mind or neuroscience tend to have this or that opinion about it.

As I mentioned above, the debate about the relevance of XPhi to philosophy is still raging, and it is easy to find a number of position papers on the positive side, and a number of negative commentaries on the other. Here I will briefly sample two recent commentaries, a negative one by Timothy Williamson (2013) and a more positive one by Alan Love (2013). The reason these two contributions are interesting is because, while they both refer to the same book (Alexander 2012, though Love also reviews another volume by Cappelen (2012), which is itself critical of XPhi), together they manage to capture my own range of reactions to the very idea and practice of XPhi, which could be summarized as follows: it’s an interesting idea, and I’d like to keep an open mind about it; but the proof is in the pudding, and so far much of the literature on XPhi seems to be interesting for social scientists but a bit of a side issue for philosophers.

Let us begin with Williamson, then. For him, philosophers have always accepted the idea that empirical findings are relevant to their interests. For instance, quite obviously, scientific experiments testing the theory of Special Relativity bear on philosophical discussions of time. Or consider how split-brain experiments in neuroscience inform philosophical discussions about personal identity. The list is a very long one indeed, but of course the idea of XPhi is to train the microscope onto philosophy itself, so to speak. Yet, Williamson points out that in a sense the XPhi project is not new, citing the example of Arne Næss sending out questionnaires about the concept of truth in the 1930s, or discussions about the relevance of philosophy of language to the way language is actually used back in the 1950s. In fact, I would say that we can push all the way back to Hume for a clear forerunner of XPhi. After all, he wished to turn philosophy upside down and remodel it after the very successful natural philosophy practiced by the like of Newton. The fact that Hume himself didn’t do any experiments did not stop him from proposing his famous “fork,” according to which only books containing mathematics or empirical evidence are worth not being burned (has it has been observed time and again, Hume’s own treatises would not survive the fork, which would be a shame for the world’s literature).

Williamson then takes on a perennial workhorse of XPhi criticism of philosophical practice: the use (and abuse) of intuitions. I will return to this crucial subject in more detail below, but for now suffice it to say that Williamson suggests that philosophical “intuitions” are a kind of judgment, their nature being not very different from that of judgments made in everyday life or in the natural sciences, i.e. a type of non-explicit inference (which can, however, be made explicit upon request). This being the case, a good deal of XPhi’s criticism of the practice of contemporary philosophy loses at the least some of its bite. Alexander, the target of Williamson’s criticism, argues that further empirical evidence needs to be brought forth any time a philosopher deploys an intuition as a starting point for a discussion, in case someone is not convinced by, or does not share, that intuition. But, replies Williamson, this is true for any premise at all, regardless of whether it plays a role in philosophical, scientific, or everyday discourse — and quite independently of whether we label that premise with the word “intuition” or not.

As we have seen above, a standard response to XPhi criticisms of philosophical practice is that the judgments of experts (i.e., philosophers) about philosophical questions is a different matter from, and more reliable than, the judgment of laypeople, which tend to be the overwhelming (though, lately, not exclusive) target of XPhi studies. When XPhi exponents like Alexander counter that this leads one into a regress because there is no guarantee that expert judgment is reliable, Williamson and others can reply that that criticism risks sliding into a generic skeptical argument, since no discipline can offer that sort of guarantee of what its properly trained experts say.

My friend Alan Love’s take on XPhi in general, and on Alexander’s book in particular, is more charitable than Williamson’s, and may in fact point toward a constructive way for XPhi supporters and critics to move forward. Alan begins by suggesting that it is instructive to ask ourselves what “image” of science XPhi actually uses, and whether such image does a good job of translating into the sort of activity that is embodied by philosophical inquiry.

Much hinges, again, on the issue of deployment of intuitions in philosophy. For Alexander (2012) philosophers use intuition all the time, especially as “data” to “test” their notions, but for authors such as Cappelen (2012) philosophers hardly use intuitions at all. Cappelen thinks that the appearance of the word “intuition” in talks, papers and books by philosophers is epiphenomenal, as Love puts it: i.e., much of what philosophers say could be rephrased without calling on intuitions at all, and stand just the same. In some cases philosophers say things like “it is intuitive that” as a shorthand for something they won’t argue for on that occasion, but instead use as a starting point for whatever follows. The implicit statement being that one can always go back and argue for that premise, or even check the matter out empirically, if need be.

Given this discrepancy, according to Love, XPhi adopts a particular “image” of science in order to compare it to what philosophers do (and find the latter wanting), namely that of an activity based on hypothesis testing and theory confirmation. Interestingly, this image is widely emulated in the social sciences (from which XPhi takes its inspiration), but Love correctly points out that philosophers of science have uncovered more than one image for science (e.g., Godfrey-Smith 2006; Wimsatt 2007), an alternative being that of an activity that aims at exploratory inquiries in order to characterize natural phenomena. Alan then suggests that philosophy is better seen as a conceptual equivalent of this exploratory activity, rather than one engaging in hypothesis testing.

This observation, I believe, is a potential breakthrough in the debate, as it naturally leads to a pluralistic view of how philosophical inquiry proceeds: it deploys a number of tools (including XPhi) to explore whatever territory is of interest. It also means that it is fruitless to look for methods or questions that are “eminently philosophical in nature,” as philosophy is not a natural kind (any more than science is, really), and it is best thought of as contiguous to (but not subsumed into) science, with an emphasis on conceptual rather than empirical space — essentially what I’ve been arguing throughout this book.

Love also points out that old canards such as “philosophy always deals with the same questions” are really red herrings. For instance, biology has been dealing with the problem of how embryos develop from the time of Aristotle (the same old question: Lennox 2011), but of course a number of very different ways of framing and tackling that question have seen the light between the History of Animals and modern research in evolutionary developmental biology (Müller & Newman 2005; Love 2009). Analogously, says Love, “We might characterize philosophical problems as stable with respect to certain themes but changing with respect to their shape and structure.” He explicitly arches back to James’ conception of philosophy (Bordogna 2008) as captured in the following quote: “philosophers should live at the boundaries of disciplines, being perpetually nomadic and constantly inserting themselves into the methodological business of other disciplines through appropriation and criticism.”

In the end, I too favor an “image” of philosophy that is distinct from yet contiguous with that of science, and where philosophers are not so much into the business of producing testable theories but rather to articulate useful “accounts” or frameworks to move debate forward on this or that particular issue. XPhi certainly does have the potential to contribute to that conversation, and should most definitely not be dismissed out of hand. But talk of “movement” and publication of position papers should probably be superseded by run of the mill positive contributions to the philosophical literature, to be evaluated on their own merits by philosophers who are engaged with the specific questions, from free will to the nature of consciousness and so forth.

Yet another challenge: the rise of the Digital Humanities

A very different sort of challenge to the traditional conception of philosophical inquiry comes from the idea of the so-called “Digital Humanities” (DH). This is a complex issue, which includes both administrative pressures on academic departments to “perform” according to easily quantifiable measures and a broader cultural zeitgeist that tends to see value only in activities that are quantitative and look sciency (the broader issue of scientism [44]). I will not comment on either of these aspects here. Instead, I will focus on some basic features of the DH movement (yes, it is another “movement”) and briefly explore its consequences for academic philosophy.

One of the most vocal advocates of DH in philosophy is Peter Bradley, who has expressed his disappointment that too few philosophers attend THATCamp, The Humanities and Technology Camp, which, as its web site explains, “is an open, inexpensive meeting where humanists and technologists of all skill levels learn and build together in sessions proposed on the spot.” [45] This is odd because, as Bradley points out [46], philosophers have been developing digital tools for some time, including the highly successful PhilPapers [47], an increasingly popular database of published and about to be published technical papers and books in philosophy; the associated PhilJobs [48], which is rapidly becoming the main, if not the only, source one needs to find an academic job in philosophy; and a number of others.

Despite this, philosophers make surprisingly little use of computational tools, such as Google’s Ngram Viewer [49] (more on this below), which Bradley claims is a shame. As an example of its utility, he ran a quick search on the occurrence of the words “Hobbes,” “Locke,” and “Rousseau,” and obtained a diagram clearly showing their “relative importance” from 1900 onwards, as measured by the appearance of these philosophers’ names in books that have been digitized by Google. The result was that Locke and Rousseau have always battled it out while enjoying a significant advantage over Hobbes, and further that Rousseau was ahead of his English rival between the 1920s and ‘50s, but the opposite has been true since the late ‘70s. Now, I don’t know whether scholars of early modern philosophy would agree with such results, but I decided to play with Ngrams myself to get a taste of the approach.

I must say, it is rather addictive, and sometimes really satisfying. For instance, a (non- philosophical) comparison of Beethoven, Mozart, the Beatles and the Rolling Stones led to precisely the outcome I expected: Beethoven and Mozart are between two and ten times more “important” than the Beatles or the Rolling Stones, with Beethoven usually in the lead (except toward the very end of the 20th century), and the Beatles beating the Stones by a comfortable margin. (Incidentally, Britney Spears barely made an appearance in a 2000-2008 search, and was almost 20 times less popular than Beethoven in 2008 [50]). Of course, it is more than a little debatable whether a popularity context reflected in an indiscriminate collection of books is a better assessment of these philosophers or musicians than the one that comes out of the technical literature in either field. Indeed, I’m not even sure whether the comparison between Ms. Spears and Beethoven is meaningful at all, on musical grounds. Also, as far as the philosophical example produced by Bradley is concerned, shouldn’t we at the least distinguish between the recurrence of certain names in philosophy books, books about politics, and books for a lay audience? It’s hard to imagine that they should all be counted equally, or subsumed into a single broad category. [51]

Despite these reservations, this data ought to provide fun food for thought at the least for introductory courses in philosophy (or music), and it may — when done more systematically and in a sufficiently sophisticated manner — present something worth discussing even for professionals in the field. And the data certainly shouldn’t be dismissed just because it is — god forbid! — quantitative. As in the case of XPhi discussed above, the proof is in the pudding, and the burden of evidence at the moment is on the shoulders of supporters of the Digital Humanities. Bradley, for instance, does suggest a number of other applications, such as pulling journal abstracts from the now increasingly available RSS feeds and run searches to identify trends within a given discipline or subfield of study. This actually sounds interesting to me, and I’m looking forward to seeing the results, though one also needs to be mindful that these exercises can all too easily become much more akin to doing sociology of philosophy rather than philosophy itself (exactly the same point made earlier about XPhi).

Lisa Spiro built on Bradley’s points [52], noticing that by 2013 the National Endowment for the Humanities Office of Digital Humanities had awarded only five grants to philosophers at that point (four of them to the same person!), and that the American Philosophical Association meeting that year only featured two sessions on DH, compared to 43 at the American Historical Association and 66 at the Modern Language Association meetings (although, as the author notes, the latter two professional societies are much larger than the APA). Even so, as Spiro herself and several commenters to her article point out, this may be yet another case of philosophers engaging in hyper-criticism of their own discipline (see Chapter 1) while not recognizing their achievements. Besides the already noted PhilPapers, PhilJobs, etc., philosophy can boast one of the very first online open access journals (The Philosopher’s Imprint [53]), the first and only philosophy of biology online open access journal (Philosophy & Theory in Biology [54]), and what I think is by far the best online, freely available, scholarly encyclopedias of any field, the Stanford Encyclopedia of Philosophy and the Internet Encyclopedia of Philosophy [55], the quality of whose entries is so high that I regularly use them as either an entry point into a field or topic different from my own or as a quick reminder of where things stand on a given issue. The SEP, incidentally, actually predates Wikipedia!

While a case can be made that philosophers “went digital” before it was cool, and that there is not much reason to think they’ll retreat or disengage any time soon, it is worth broadening the discussion a bit, and ask ourselves what basic arguments in favor and against the whole DH approach have been advanced so far. As in the case of XPhi, the literature is already large, and getting larger by the month. Nonetheless, here is my preliminary attempt at summarizing what some of the defenders and critics of DH have to say at a very general level of discourse.

Just like in any discussion of “the old fashioned ways” vs the “new and exciting path to the future,” there is hype and there is curmudgeonly resistance. An example of the first one — in the allied field of literary criticism — is perhaps an article by Bill Benzon (2014), which begins by boldly stating that “digital criticism is the only game that’s producing anything really new in literary criticism.” It is obvious to retort that new may or may not have anything at all to do with good, however.

The standard example mentioned in this context is the work of Stanford University Franco Moretti, a champion of heavily data-based so-called “distant reading.” The idea, which can easily be transferred to philosophy (though, to my knowledge, has not been, yet) is that instead of focusing on individual books (classical, or “close” reading), one can analyze hundreds or thousands of books at the same time, searching for patterns by using the above mentioned Ngram Viewer or similar, more sophisticated, tools. It seems, however, that this cannot possibly be meant to replace, but rather to complement the classical approach, unless one seriously wants to suggest that we can understand Plato without reading a single one of his dialogues, for instance. Indeed, distant “reading” is really a misnomer, as no reading is actually involved, and the term may lead to unnecessarily confrontational attitudes. The sort of questions one can ask using massive databases is actually significantly different from the “classic” questions of concern to literary critics, philosophers, and other humanists. Some of the times these new questions will indeed nicely complement and integrate the classical approach and address the same concerns from a different standpoint, but in other cases they will simply constitute a change of the subject matter (which is not necessarily a bad thing, but does need to be acknowledged as such).

Data-based techniques can even be applied to single works of literature, as shown by Moretti’s “abstract” reconstruction of the relationships among the characters of Hamlet. The issue is whether a professional literary critic will learn something new from the exercise. Is it surprising, for instance, that Hamlet emerges as the central figure in the diagram (and the play)? Or that he is very closely connected to the Ghost, Horatio, and Claudius, while at the same time relating only indirectly to, say, Reynaldo? I’m no Shakespearean scholar, so I will lead that judgment to the pertinent epistemic community.

Regardless, Benzon makes important points when he places the rise of distant reading in the context of the recent history of literary criticism. To begin with, “reading” in this sense is actually a technical term, referring to explaining the text. And the field has seen a number of more or less radical moves in this respect throughout the second half of the 20th century and beyond. Just think of the so-called New Critics of the post-WWII period, defending the autonomy of the text and the lack of need to know anything about either the author or the cultural milieu in which she wrote the book. And then we have the infamous “French invasion” of American literary criticism, which took place at a crucial 1966 conference on structuralism in Baltimore. Similar considerations have been made concerning the split between analytic and continental philosophy throughout the 20th century, or the rise of postmodernism and the ensuing “science wars” of the 1990s (Chapter 2). Indeed, the parallels between the recent history of philosophy and literary criticism as academic fields are closer than one might expect. Just like philosophers have gone through a “naturalistic turn” (Chapter 3), to the point that many of us nowadays simply wouldn’t even think of ignoring much of what is done in the natural sciences, especially physics, biology and neuroscience, so too a number of literary critics have embraced notions from cognitive science and evolutionary psychology — as problematic as this move sometimes actually is [56].

An entirely different take on the Digital Humanities is the one adopted, for instance, by Adam Kirsch (2014) [57]: at least part of the problem with DH is that the concept seems rather vague. Kirsch points out that plenty of DH conferences, talks and papers are — symptomatically — devoted to that very question (just as, I cannot resist to note, in the parallel case of experimental philosophy). Is DH, then, just a general umbrella for talking about the impact of computer technologies on the practice of the humanities? That seems too vague, and at any rate, philosophy is doing rather well from that perspective, as we have already seen. Or is it more specifically the use of large amounts of data to tackle questions of concern to humanists? In that respect philosophy may indeed be behind, but it isn’t at all clear whether analyses of large data sets on, say, recurrence of words or names in philosophical works is going to be revolutionary (I doubt it), or just one more tool in the toolbox of philosophical inquiry (which seems more sensible).

Kirsch’s criticism is rooted in his reaction to claims by, for instance, the authors of the Digital_Humanities “manifesto” (Burdick et al. 2012): “We live in one of those rare moments of opportunity for the humanities, not unlike other great eras of cultural- historical transformation such as the shift from the scroll to the codex, the invention of movable type, the encounter with the New World, and the Industrial Revolution.” It is rather difficult to refrain from dismissing this sort of grandiosity as hype, which sometimes becomes worrisome, as in the following bit from the same book: “the 8-page essay and the 25-page research paper will have to make room for the game design, the multi-player narrative, the video mash-up, the online exhibit and other new forms and formats as pedagogical exercises.” If by “making room” the authors mean replace, then I’m not at all sure this is something desirable.

And just in case you think this is unrepresentative cherry picking, here is another indicative example uncovered by Kirsch, this time from Erez Aiden and Jean-Baptiste Michel (2013), the very creators of the Ngram Viewer: “Its consequences will transform how we look at ourselves. ... Big data is going to change the humanities [and] transform the social sciences.” And yet, the best example these authors were able to provide to back their claim was a demonstration that the names of certain painters (e.g., Marc Chagall) disappeared from German books during the Nazi period — a phenomenon well known to historians of art and referred to as the case of the “degenerate art” (Peters 2014). Indeed, it is the very fact that this was common knowledge that led Aiden and Michel to run their Ngram search in the first place.

Kirsch also takes on the above mentioned Moretti as a further case in point, and particularly his “Style, Inc.: Reflections on 7,000 Titles” (Moretti 2009). There the author practices data analysis on 7,000 novels published in the UK between 1740 and 1850, looking for patterns. One of the major findings is that during that period book titles evolved from mini-summaries of the subject matter to succinct, reader-enticing short phrases. Which any serious student of British literature would have been able to tell you on the basis of nothing more than her scholarly acquaintance (“close” reading) with that body of work. This does by no means show that DH approaches in general, or even distant reading in particular, are useless, only that the trumpet’s volume ought perhaps to be turned a few notches down, and that DH practitioners need to provide the rest of us with a few convincing examples of truly innovative work leading to new insights, rather than exercises in the elucidation of the obvious.

Here is another example of DH hype, this time specifically about philosophy: Ramsay and Geoffrey Rockwell (2013) write in their “Developing Things: Notes Toward an Epistemology of Building in the Humanities”: “Reading Foucault and applying his theoretical framework can take months or years of application. A web-based text analysis tool could apply its theoretical position in seconds.” As Kirsch drily notes, the issue is to understand what Foucault is saying, which is guaranteed to take far more than seconds, as anyone even superficially familiar with his writings will readily testify.

In general, I think Kirsch hits the nail on the head when he points out that there are limits to quantification, and in particular that a rush to quantify often means that one tends to tackle whatever it is easy to quantify and ignore the rest [58]. But much humanistic, and philosophical, work is inherently qualitative, and simply doesn’t lend itself to statistical summaries such as word counts and number of citations. The latter can be done, of course, but often misses the point. And remarking on this, as Kirsch rightly puts it, is “not Luddism; it is intellectual responsibility.”

Another notable critic of DH is Stephen Marche (2012) who, somewhat predictably at this point, again takes on Moretti’s distant reading approach. Marche does acknowledge that data mining in the context of distant reading is “potentially transformative,” but he suggests that so far at the least this potential has resulted into a shift in attitude more than the production of actually novel insights into literary criticism. He objects to the “distant” modifier in distant reading, claiming that: “Literature cannot meaningfully be treated as data. The problem is essential rather than superficial: literature is not data. Literature is the opposite of data.” Well, not so fast. I don’t see why it can’t be both (and the same goes for philosophy, of course), but I do agree that the burden of evidence rests on those claiming that the old ways of doing things have been shuttered. Then again, critics like Marche virtually shoot themselves in the foot when they go on with this sort of barely sensical statements: “Algorithms are inherently fascistic, because they give the comforting illusion of an alterity to human affairs.” No, algorithms are not inherently fascistic, whatever that means. They are simply procedures that may or may not be relevant to a given task. And that’s where the discussion should squarely be focused.

There are also, thankfully, moderate voices in this debate, for instance that of Ben Merriman (2015), who positively reviewed two of Moretti’s books (together with Joskers’ Macroanalysis: Digital Methods and Literary History and Text Analysis with R for Students of Literature). Merriman observes that, at the least at the moment, a lot of work in the Digital Humanities is driven by the availability of new tools, and that the questions themselves remain recognizably humanistic. I don’t think this is a bad idea, and it finds parallels in science: the invention of the electron microscope (or, more recently, of fMRI scanning of the brain), for instance, initially generated a cottage industry of clearly tool- oriented research. But there is no question that electron microscopy (and fMRI scanning) did contribute substantially to the advancement of structural biology (and brain science).

Merriman points out that Moretti and Joskers are more ambitious, explicitly aiming at setting a new agenda for their field, radically altering the kind of questions one asks in humanities scholarship. Some of the examples provided do sound genuinely interesting, if not necessarily earth-shattering: distant reading allow us to study long-term patterns of change and stability in literary genres, for instance, or to arrive at surprisingly simple taxonomies of, say, types of novels (apparently, they all pretty much fall into just six different structural kinds). Some of this work, again, will confirm and expand on what experts in the field already know, in other cases it may provide new insights that in turn will spur new classical scholarship. Merriman refers to the results achieved by DH so far as “mixed,” and that seems to me a fair assessment, but not one on the basis of which we are therefore in a position to dismiss the whole effort as mere scientistic hubris, at the least not yet.

One interesting example of a novel result is Moretti’s claim that he has an explanation for why Conan Doyle’s mystery novels have had such staying power, despite the author having plenty of vigorous competition at the time. The discovery is that mystery novels can be analyzed in terms of how the authors handle the clues to the mystery. Conan Doyle and other successful writers of the genre all have something in common: they make crucial clues consistently visible and available to their readers, thereby drawing them into the narrative as more than just passive recipients of plot twists and turns.

Merriman, however, laments that social scientists and statisticians don’t seem to have taken notice, thus far, of the onset of DH, which is problematic because its current practitioners sometimes mishandle their new tools — for instance giving undue weight to so-called significance values of statistical tests, rather then to the much more informative effect sizes (Henson and Smith 2000; Nakagawa and Cuthill 2007) — a mistake that a more seasoned analyst of quantitative data would not make. It is for this reason, in fact, that one of the books reviewed by Merman is a how-to manual for aspiring DH practitioners. Even so, more cross-disciplinary efforts would likely be beneficial to the whole endeavor, both in literary criticism and in other fields of the humanities, including philosophy.

Speaking of the latter, distant reading is not the only approach that legitimately qualifies as an exercise in the Digital Humanities, and an interesting paper by Goulet (2013) is a good example of the potential value of DH for scholarship in philosophy. The author presents some preliminary analyses of data from a database of ancient Western philosophers, spanning the range from the 6th Century BCE to the 6th Century CE. The survey concerns about 3,000 philosophers, confirming some well known facts, as well as providing us with novel insights into that crucial period of the history of philosophy. For instance, it turns out that about 3.5% of the listed philosophers were women — a small but not insignificant proportion of the total. Interestingly, most of these women were associated with Epicurus’ Garden or with the Stoics of Imperial Rome. Goulet was able to identify a whopping 33 philosophical schools in antiquity, but also to show quantitatively that just four played a dominant role: the Academics-Platonists (20% of total number of philosophers), the Stoics (12%), the Epicureans (8%), and the Aristotelian-Peripatetics (6%), although he notes an additional early peak for the Pythagoreans (13%), whose influence rapidly waned after the 4th Century BCE. Goulet is able to glean a wealth of additional information from the database, information that I would think from now on ought to be part of any serious scholarly discussion of ancient Greco-Roman philosophy.

So, will the DH revolutionize the way we do philosophy? I doubt it. Will they provide additional tools to pursue philosophical scholarship, perhaps together with some versions of XPhi? Very likely. And it is this idea of a set of disciplinary tools and what they can and cannot do that leads us into the next section, where I briefly survey some other instruments in the ever expanding toolbox of philosophical inquiry. The one provided here is not an exhaustive list, and it does not include a treatment of more general approaches that philosophers share with scholars from other fields. But I think it may be useful nonetheless to remind ourselves of and reflect on what the tools of the trade are, in order to complete our analysis of what philosophy is and how it works.

The tools of the trade

We have already discussed at some length one important — if controversial — philosophical tool: the deployment of intuitions. I find it interesting that rarely critics and defenders of the use of intuition in philosophy bother to look at the broader literature on intuitions in cognitive science, which is actually significant and covers fields as diverse as chess playing, nursing and the teaching of math. I have discussed some of this literature elsewhere (Pigliucci 2012), but a quick recap may be useful in this specific context.

The very word comes from the Latin intuir, which aptly means “knowledge from within.” It is no longer considered a mysterious faculty of the human mind, as it has been the proper object of study in the cognitive sciences for a while (Hodgkinson et al. 2008). The first thing to realize is that there doesn’t seem to be any such thing as a generic ability of intuition. That is, when people say that they are “intuitive” they are likely fooling themselves, or they are mislabeling a more specific aptitude they have developed. Intuition, as it turns out, is domain specific: the more we acquire expertise and familiarity with a subject matter, the more we develop correct intuitions about that subject matter. Intuition — as generally understood — is simply a form of rapid (Kahneman 2011, following up on an initial suggestion by William James) subconscious processing of information, which is offered to our slow, conscious mental processing for further checking and refinement.

This is why the literature on expertise — and in particular philosophical expertise — becomes relevant (Ross 2006; for a philosophical take on it, see Selinger and Crease 2006). Expertise develops in distinct phases, almost regardless of the specific field, moving from novitiate to proficiency to actual mastery (in an academic context, think of the roughly analogous progression from undergraduate to graduate studies and then to the professional level). The latter may require about a decade to achieve, and results in complex webs of structured knowledge in one’s mind, a phenomenon that makes it possible for experts to quickly assess a situation (or an argument), see the pitfalls, and develop a solution (or a counter-argument).

Perhaps the best studies on expertise have been conducted on chess masters (e.g., Charness 1991; Gobet and Simon 1996), in part because the task is clearly delineated and in part because it is straightforward to measure one’s proficiency in that field. When a chess master is faced with a set situation (i.e., a chess problem) that developed organically via an actual game she will have little difficulty quickly arriving at the best moves. Interestingly, when asked why she deployed certain moves rather than others, the master will often reflect on the question and slowly reconstruct a logical answer: she did not consciously, explicitly, go through those steps, because she reacted intuitively. But she is nonetheless capable of providing a reasonable justification of what she did. Even more interestingly, it has been demonstrated that chess masters’ intuitions often fail whenever they are presented with a set situation that did not develop from an actual game, i.e., with an artificial scenario that could not possibly have contributed to their store of subconscious knowledge. Of course, I am not saying that there is a direct equivalency between these studies on intuition and what philosophers call by that name. But if philosophical intuition is — at the least in some sense — something akin to the more general phenomenon that goes by the same name (as, for instance, XPhi supporters often claim), then this sort of literature ought to be taken into account.

Perhaps it is instructive at this point to briefly go back to XPhi and the issue it raises about the use of intuitions in philosophy. After having drawn a parallel with the deployment of intuitions in other fields, such as arithmetic and geometry, Sosa (2009, 101) provides a working definition of intuition for the purposes of philosophical inquiry: “to intuit that p is to be attracted to assent simply through entertaining that representational content. The intuition is rational if and only if it derives from competence, and the content is explicitly or implicitly modal (i.e., attributes necessity or possibility).” Please notice the emphasis on competence, that is, on expertise.

In response to XPhi papers showing the effect of cultural differences and/or “framing” on people’s intuitions about philosophical concepts such as moral desert, free will (but, apparently, not knowledge! See Machery et al. 2015), etc., a few observations may now be made in addition to our previous discussion. First, such differences may result from the lay subjects not having thought about those topics much (unlike, presumably, professional philosophers) — i.e., they are not experts on the subject matter at hand. Second, it is not really surprising that different background conditions, including individuals’ assumptions about the cases being presented to them, will cause variation in the responses (a point also made by Sosa); research on intuition has shown, as we have seen in the case of chess masters, that different conditions legitimately elicit different intuitions, and that even experts can be laid astray when faced with highly artificial scenarios. But of course that is precisely what careful philosophical unpacking of concepts is supposed to explore and deal with.

Moreover, according to Goldman (2007) the use of “intuition” as a term to describe how philosophers use hypothetical examples in their reasonings is actually of fairly recent vintage, tracing to Chomsky’s methodological discussions in linguistics. Goldman has also spent a significant amount of effort thinking about intuitions in philosophy. He examines a number of possible “targets” of philosophical intuitions: Platonic forms, natural kinds, Fregean concepts, concepts in the psychological sense, and “shared” concepts. I find his discussion of Fregean concepts particularly illuminating. He defines these as “abstract entities of some sort, graspable by multiple individuals. These entities are thought of as capable of becoming objects of a faculty of intuition, rational intuition.” He cites Bealer (1998) as explicating what it means to grasp a concept by rational intuition: “[W]hen we have a rational intuition — say, that if P then not not P — it presents itself as necessary; it does not seem to us that things could be otherwise; it must be that if P then not not P.”

Goldman himself, however, prefers to talk about the last two types of targets, psychological and shared concepts, as particularly relevant to philosophical discourse. A psychological concept is a mental representation by a particular individual, and that individual will possess certain intuitions about the correct and incorrect usage of that concept relatively to how she understands the concept itself. This becomes useful once Goldman generalizes from psychological to shared concepts, which originate when there is substantial agreement within a community of individuals on the (correct and incorrect) usage of a given psychological concept. Within that community, people may then decide that some individuals — by virtue of their specific training — are better, more reliable, at deploying a certain concept. These individuals are acknowledged as experts in the usage of that concept, and their intuitions about the concept become more valuable than other people’s intuitions. You see where this is going: if the concept is, say, free will, then the community of experts is made of philosophers who have thought hard and long about free will (which excludes not just laypeople, but also philosophers who do not have expertise in philosophy of mind and metaphysics). [59]

What I have proposed so far, then, is to recast the debate about philosophical intuitions within the more general assessment of expert intuitions, about which there is a significant cognitive science literature. It also makes sense to survey philosophers’ take on what intuitions are and how they are deployed within their profession, which is precisely what Kuntz & Kuntz (2011) have done. They point out a crucial distinction that is often lost in discussions about intuition: that philosophers actually use their intuitions for two different purposes, in a “discovery” and in a “justification” mode — only the latter being typically addressed by critics of philosophical intuitions (but see my earlier discussion of Love 2013, and his framing in terms of complementary “images” of science).

Kuntz & Kuntz conducted an online survey of 282 philosophers, focusing on what they think about intuitions in their profession. To begin with, about 51% of participants said that intuitions are useful for justificatory purposes in philosophical analysis, while a whopping 83% said that are useful for exploratory analysis. Moreover, about 70% of respondents said intuitions are not necessary for justification. These statistics paint a picture that is somewhat at odds with the common criticism of the “ubiquitousness” of intuitions as “data” in philosophical discourse. The same authors provided their subjects with seven different accounts of intuitions, and it is instructive to see that two of these were given the highest rank by a majority of respondents: “Judgment that is not made on the basis of some kind of observable and explicit reasoning process” and “An intellectual happening whereby it seems that something is the case without arising from reasoning, or sensorial perceiving, or remembering.” Another of the accounts on offer received by far the lowest ranking: “The formation of a belief by unclouded mental attention to its contents, in a way that is so easy and yielding a belief that is so definite as to leave no room for doubt regarding its veracity.” [60] The first two accounts (but not really the latter) are compatible with cognitive scientists’ definition of intuition and the target of their empirical research. So, intuitions — re-conceptualized as they normally are in the cognitive science literature — remain an important tool for the philosopher, a tool that is characterized by the same pros and cons as intuitions in any other field of inquiry or, indeed, in everyday life. Crucially, it seems that a majority of philosophers uses intuitions just the way they are supposed: in an exploratory rather than justificatory fashion. While in science the justification is anchored by empirical evidence, in philosophy it is the result of “unpacking,” i.e., carefully and explicitly analyzing the initial intuition (moving from Kahneman’s system I to his system II, if you will).

Intuition, of course, is not the only tool available to the professional philosopher. Others include the method of analysis, counterfactual thinking, reflective equilibrium, and thought experiments. These are all actually related to each other (and to intuitions!), so a linear discussion of each in turn is by necessity a bit artificial. Nonetheless, I think it will be useful to complete my analysis of what philosophical inquiry consists of and how it is conducted.

Beany (2009) provides a convenient overview of the so-called method of analysis, defining it as “a process of isolating or working back to what is more fundamental by means of which something, initially taken as given, can be explained or reconstructed,” and in that sense its applicability clearly goes well beyond what nowadays is referred to as “analytic” philosophy (Chapter 2). Socrates, for one, was certainly doing analysis in Beaney’s sense. As the author correctly points out, it is misconceived to think of, say, Wittgenstein’s criticism of logical atomism, or of Quine’s rejection of the analytic-synthetic distinction as blows to the method of analysis in philosophy, since such criticisms were aimed at very narrow conceptions of that method. Indeed, Beaney identifies three different components of philosophical analysis, all of which are likely applied in combination in the course of actual philosophical practice: decompositional (aiming at unpacking the components of a concept and analyzing them individually), regressive (working back to first principles), and interpretive (translating a concept into a logically more rigorous form). Much of this goes back to the Greeks, and in fact Beaney traces it to the early influence of geometry, which made a crucial impression on thinkers from Plato on, though the development of what we call Euclidean geometry is actually a result of this, not a cause (Euclid’s Elements date from circa 300 BCE, after Plato and Aristotle).

Beaney remarks that regressive analysis was the dominant form of the method in ancient Greece, and that we had to wait until the medieval period to see the development of interpretive analysis. We then see all three approaches deployed in Buridan’s Summulae de Dialectica (1330-40; see Zupko 2003, 2014). Even so, the decompositional approach to analysis obtained its most famous formulation with Descartes, in Rules for the Direction of the Mind (1684), where he says: “If we perfectly understand a problem we must abstract it from every superfluous conception, reduce it to its simplest terms and, by means of an enumeration, divide it up into the smallest possible parts” (Rule 13). As Beaney points out, it is not by chance that Descartes admitted to be influenced by geometry, to which he of course made the novel contributions that made him justly famous: “Those long chains composed of very simple and easy reasonings, which geometers customarily use to arrive at their most difficult demonstrations, had given me occasion to suppose that all the things which can fall under human knowledge are interconnected in the same way” (Discourse on Method, 1637 /2000). From there, decompositional analysis continued its good run well into early modern philosophy with Kant.

By the 20th century, according to Beaney, both so-called analytical and continental philosophy (Chapter 2) had gone beyond decompositional analysis, with the continentals’ phenomenological approach being analogous to conceptual clarification, while Hegel can be thought of as employing regression. We have to remember that analytic philosophy in the strict sense is a new beast that originated with Frege, Russell and others, and which depends on logical analysis as made possible by contemporary logic (especially predicate logic), with the term “analytic” once again reminding us closely of geometry, more so than previous uses of the decompositional approach.

Let me now turn briefly to the use of counterfactual thinking. In his Presidential address to the Aristotelian Society in 2004, Timothy Williamson (2005) pointed out that so-called “armchair philosophizing” is chronically seen as a virtue by what he labeled “crude rationalists” and, symmetrically, a vice by what he referred to as “crude empiricists.”As Aristotle himself would have readily agreed, wisdom must lie somewhere in between. Williamson makes exceedingly clear what the problem is when he says, citing the example of analytic metaphysicians (but, really, it could be any branch of philosophy): “[they] want to understand the nature of time itself, not just our concept of time, or what we mean by the word ‘time’” (p. 2), which means that we must pay attention to the empirical, although the idea of philosophizing about it is precisely that the empirical by itself isn’t going to provide us with a satisfactory answer either.

Williamson presents a detailed discussion of Gettier-type cases in the epistemology of truth (see Chapter 6) as instances of the usefulness of counterfactual thinking, which eventually brings him to the observation that “examples [used to explore our intuitions] are almost never described in complete detail; a mass of background must be taken for granted; it cannot all be explicitly stipulated” (p. 6). He then suggests — rightly, I think — that the deployment of counterfactuals is not distinctive of philosophy: both everyday and scientific reasoning make use of them all the time. For instance, if we say “there are eight planets in the solar system” we are implicitly assuming the counterfactual that if there were more planets in our neighborhood we would have discovered them by now. The fact that we do not have discovered additional planets does not logically imply that there are none, so the counterfactual conditional plays the role of allowing us what we understand to be a provisional conclusion, revisable at any time in light of new evidence. The very same role is played by counterfactuals in philosophical reasoning: they imply a “as far as we can tell given what we know” condition. Which leads Williamson to argue that intuitions and counterfactuals in philosophy, along the lines of those famously deployed in discussions of Gettier cases, are examples of human judgment no different from the judgment we reach in other applications, it is the specific subject matter, not the method, that is philosophic: “we have no good reason to expect that the evaluation of ‘philosophical’ counterfactuals ... uses radically different cognitive capacities from the evaluation of ordinary ‘unphilosophical’ counterfactuals. We can evaluate [these counterfactuals] without leaving the armchair; we can also evaluate many ‘unphilosophical’ counterfactuals without leaving the armchair” (p. 13), which ought to take at the least some of the bite out of the standard criticisms of armchair philosophizing. To reiterate: philosophical intuition is not a special cognitive ability, and does not, therefore, demand special defense or scrutiny.

Indeed, Williamson’s conclusion so nicely dovetails with my main thesis in this book that it is worth (to me) to quote him again in some detail (p. 21): “Both crude rationalism and crude empiricism distort the epistemology of philosophy by treating it as far more distinctive than it really is. They forget how many things can be done in an armchair, including significant parts of natural science ... That is not to say that philosophy is a natural science, for it also has much in common with mathematics.” Exactly.

I turn next to another staple of the philosopher’s toolbox: reflective equilibrium. Although the term has reached wide popularity in philosophy as deployed by John Rawls (1971) in his A Theory of Justice, reflective equilibrium is a general feature or method of philosophical reasoning, formalized in recent times by Nelson Goodman in his Fact, Fiction and Forecast (1955) in the context of inductive logic (though Nelson didn’t use the specific phrase “reflective equilibrium”). Daniels (2003) defines it fairly clearly in this fashion: “The method of reflective equilibrium consists in working back and forth among our considered judgments (some say our ‘intuitions’ [61]) about particular instances or cases, the principles or rules that we believe govern them, and the theoretical considerations that we believe bear on accepting these considered judgments, principles, or rules, revising any of these elements wherever necessary in order to achieve an acceptable coherence among them.” Notice Daniels’ emphasis on a coherentist approach to epistemology, as opposed to a foundationalist one. As we discussed especially in Chapter 3, in the context of Quine’s “web of belief,” coherentism seems a much more sensible way of approaching knowledge and judgment, provided that at the least some of the elements of our epistemological web are empirical facts, for the very compelling reason that it is empirical facts that allow us to move from conceptual space (where often there are a number of equally logically coherent scenarios or approaches to a problem) to the world as it actually is (where I still presume most of us will agree that things are either one way or another, but not both).

I see reflective equilibrium in conceptual space as in a way analogous to inference to the best explanation in empirical space. Neither is a perfect approach, nor does it provide any guarantee of success, but they are very sensible tools for navigating both spaces. Inference to the best explanation, for instance, suffers whenever one has not conceived of better alternative scenarios, in which case one is stuck with a “best of a bad lot” situation; it also suffers whenever insufficient or low quality data is all that is available. Analogously, reflective equilibrium doesn’t work very well if one fails to consider better (i.e., more coherent with the available facts and assumed notions) scenarios, or if one’s knowledge of the relevant elements is insufficient or faulty. Nevertheless, these are the sort of problems that negatively affect (and impose limits upon) any kind of human reasoning, about either matters of fact or relations of ideas (or anything else), as Hume would put it.

Daniels (2003) helpfully distinguishes between a narrow and a wide form of reflective equilibrium, though I think it is better to treat these as two points of reference along what is essentially an epistemic continuum (analogous, I suspect, to the difference between Duhem’s and Quine’s theses — respectively narrow and wide — as discussed in Chapter 2). Daniels’ example of narrow reflective equilibrium is the case of rationing of medical care according to the age of the patient. At first glance, one might think that this is similar to rationing by, say, sex, or ethnic background, which would, presumably, be unethical. However, further reflection shows that age is a different biological phenomenon from the other two (for instance, because we all age, but people can’t change sex without medical assistance, and simply don’t change ethnic background). Rationing care by age, therefore, does not have to be discriminatory (and it may thus be morally acceptable), and it could very well turn out to be a highly sensible practice in terms of both efficacy and cost. This qualifies as a narrow type of reflective equilibrium because a large number of background assumptions and a lot of factual knowledge have been left unchallenged in order to focus on a fairly specific debate.

To move from a narrow to a wide exercise in reflective equilibrium one can contemplate the famous example of Rawls’ questioning of the very tenets of utilitarian ethics, which may have been treated instead as a background assumption in the previous instance. Wide reflective equilibrium, in other words, brings under scrutiny some of the broader axioms of our thinking. Just as in the case of the difference between (narrow) Duhem’s and (broad) Quine’s approaches in philosophy of science and epistemology, one needs to keep in mind that most actual applications will be on the narrow side of things, as only occasionally it pays off to broaden the circle of questioning that far.

Naturally, there are a number of standard criticisms to the practice of reflective equilibrium, most of which, I think, seem to miss the point. For instance, it is argued that reflective equilibrium depends on judgments (say, in ethics) that are founded on certain “intuitions” which are in themselves questionable or can be challenged. This is certainly true — with the caveats about philosophical “intuition” mentioned above — but that very same criticism applies to pretty much any human judgment, in both conceptual and empirical matters. Yes, any given judgment can be challenged, and if so then it needs to be defended, unpacked, argued for, etc.. In other words: welcome to philosophy!

A second common criticism of the method of reflective equilibrium is a special instance of the general problem with coherentist views of truth: as Hare (1973) wrote in response to Rawls, fictional scenarios (say, in a novel) can also be made coherent, but one is hardly thereby justified in accepting them as truthful. But presumably philosophers will always be concerned with how things stand in the real world, i.e. their judgments will be, as much as possible, informed by — and anchored to — our best understanding of empirical facts. Although such facts themselves are revisable, theory-dependent, etc., it is the full web of beliefs that makes reflective equilibrium a dynamic practice, whose particular status at any given moment can always be reassessed if new facts and/or arguments come to light. Compare that with the static description of a fictional scenario in a novel and the difference ought to be obvious.

A theoretically more serious, but also much less impactful in practical terms, concern is that it is actually surprisingly difficult to provide a philosophically satisfying account of the very concept of coherence. What is required for reflective equilibrium is stronger than the simple lack of straightforward logical contradictions, and is more akin to a Bayesian-type judgment as deployed in scientific inferences to the best explanation. I think, however, that the project of providing a good account of coherence can proceed of its own accord without philosophers having to await for a final outcome in order to practice reflective equilibrium, as long as they are very clear about why they think a certain set of beliefs and empirical facts is more “coherent” than another, and are willing to defend such judgment when challenged.

Another classic tool available to philosophers (and to scientists) is the thought experiment. Examples in the sciences abound, as is well known, from Newton’s bucket to Schrödinger’s cat. In fact, the very term (“Gedankenexperiment” in German) appeared to have been introduced by 19th century physicist Ernst Mach, though the approach is much older than that. As J.R. Brown (2002) points out, one of the most appealing (and, as it turns out, wrong) thought experiments was advanced by Lucretius in De Rerum Natura, where he attempted to show that space is infinite by conjuring a hypothetical scenario in which we are able to shoot a spear through the universe’s boundary. The logic is solid: if the spear goes through the boundary, then it is not really a boundary; if it bounces back then there is an obstacle that must itself be located in a portion of space beyond the alleged boundary. But Lucretius didn’t know about the possibility of spaces that are both unbounded and yet finite (Einstein 1920). The fact that the experiment eventually failed is no argument against the use of thought experiments in general: first, because other such experiments succeeded; second, because plenty of empirical experimental results are also eventually overturned by further discoveries; and third, because we still learn something about how to think about the specific matter in question (in this case, space and infinity) by contemplating why exactly the outcome of the experiment (thought or empirical) had ultimately to be rejected.

Just like the case of intuitions, however, one may reasonably ask on what grounds we rely on thought experiments, i.e., what, exactly, are the epistemological foundations of this approach to theorizing? There is a large literature on this topic, and a good recent summary of the major positions has helpfully been provided by Clatterbuck (2013). There are at least three accounts that try to make sense of how thought experiments work: they may represent an example of Platonic knowledge; they may be a pictorial form of standard inductive arguments; or they may represent a special type of induction.

Starting with the suggestion that thought experiments give us access to a Platonic realm of ideas, so that we can somehow gain a priori knowledge about the physical world in just the way we gain mathematical knowledge, the argument in defense of this position is put forward by J.R. Brown (1991), and Clatterbuck reconstructs it this way:

Premise 1. Mathematical Platonism is true.

Premise 2. Mathematical Platonism entails that numbers are outside of space or time.

Premise 3. Mathematical Platonism entails that we can have intuitive knowledge of numbers.

Premise 4. Realism about laws is true.

Premise 5. Realism about laws entails that laws of nature are outside of space and time.

Premise 6. If we can have intuitive knowledge of numbers which are outside of space and time, then we can also have intuitive knowledge of laws which are outside of space and time.

Conclusion: We can have intuitive knowledge of the laws of nature.

To unpack: Brown assumes two controversial positions in metaphysics, namely mathematical Platonism (see my skepticism about it in the Introduction) and realism about laws of nature (see Cartwright’s and others’ skepticism about that, in Chapter 4). From these two premises, and from what they logically entail, he arrives at the conclusion that we can obtain intuitive knowledge of the laws of nature, and suggests that thought experiments are one way to obtain such intuitive knowledge (there goes “intuition,” again!). The argument is valid, but it is an altogether different issue to establish the soundness of its premises.

Most scientists, I wager, would have no problem with P4, and therefore must accept also P5. P2 and P3 are tightly connected with P1, so the latter may be the obvious target of criticism. But, as we have already seen, a good number of mathematicians and philosophers of mathematics do not find mathematical Platonism to be a bizarre idea at all. Still, even if we provisionally accept mathematical Platonism, for the sake of argument, Clatterbuck suggests that the real stumbling block is actually P6: it embodies an argument from analogy, whereby mathematical truths are taken to be of the same kind as physical laws. This is metaphysically questionable, since mathematical truths are necessarily such, while physical laws appear to be only contingently true (i.e., in no possible world a given mathematical truth becomes untrue, while there are many possible worlds where our natural laws do not hold). Another way to put the point is that we routinely arrive at mathematical (and logical) truth simply by thinking about a mathematical (or logical) problem, but we usually need observations and/or experiments to gain any knowledge of the physical world — and this is because the latter is a contingent subset of a number of logically possible worlds, a subset that can only be pinpointed empirically.

A second possibility is that thought experiments are nothing but standard arguments accompanied by pictures, a position that has been defended, for instance, by Norton (2004). According to him, what Galileo, Einstein and others have been doing in this respect is simply to present an inductive or deductive argument, peppered with pictures to make it more vivid to the intended audience. The point being that the mental “pictures” (e.g., Galileo’s two bodies of different weight falling separately or linked to each other; Einstein’s beams of light) are not necessary for the argument to go through, they are just embellishments with rhetorical but no epistemic force. Essentially, Norton is being parsimonious here: if we assume that thought experiments are just standard arguments plus pictures (where the latter play no additional epistemic role), then we don’t need to invoke Platonism.

Clatterbuck, however, thinks that Norton is being too parsimonious, missing an important part of the action. Imagine a concrete problem in physics, say, the dynamics of the fall of two bodies of different weight, either linked to each other or not; we can begin by abstracting away all irrelevant or distracting factors, such as air friction that interferes with the fall of the bodies; we arrive at certain conclusions concerning the problem, in this case that Aristotelian physics applied to the hypothetical experiment leads to a logical contradiction, as Galileo did; finally, we generalize our findings to the real (i.e., not idealized) world. What we have as a result of this procedure, of course, is a thought experiment. But notice that the idealization of the circumstances played a crucial role in the construction of the experiment. That is, according to Clatterbuck, the “picture” part of the inductive reasoning we just deployed is not simply a pretty but ultimately dispensable accessory, it is a crucial aspect of what’s going on. The result is something different from, say, enumerative induction, since we don’t have to “observe” more than one case to infer our conclusions: the (idealized) case is sufficient by itself to yield a logically valid inference. The upshot is that thought experiments embody a type of inductive reasoning, but that such reasoning requires idealization or abstraction to yield the conclusion from a single instance to a generally valid class of cases. In a sense — when done well — thought experiments are more powerful than standard enumerative induction, which after all is based on always fallible collections of observations. There is much more to be said about thought experiments, including interesting discussions about what, exactly (if any!), is the difference between a thought experiment in science and in philosophy. Nonetheless, thought experiments have clearly yielded many fecund lines of inquiry, and will certainly remain an essential part of the philosopher’s toolbox.

What do philosophers think of philosophy?

I am about to wrap up my tour of what philosophy is and how it works, which has taken us throughout these seven chapters to examine subjects as disparate as the Kyoto School and Quineian webs of beliefs, the history of progress in mathematics and the various theories of truth as they apply to the explanation of scientific progress. Before some concluding remarks on the current status and foreseeable future of the discipline, however, it seems advisable to pause and reflect on what philosophers themselves think of a number of issues characterizing their own profession. As we have seen, we are often accused of endlessly posing the same questions, and of having more opinions floating around than the number of available philosophers. I have dealt somewhat with the first accusation above; as far as the second one goes, we actually have empirical data to falsify it, or at the least to question its alleged sweeping reach. Such data come from a rare survey of professional philosophers’ take on a number of philosophical questions, conducted by David Bourget and David Chalmers (2013). I think it is important for every profession to have a pulse of itself, so to speak, i.e., for its practitioners — at the least from time to time — to get a sense of where their field is and where it may be going, and in that respect, this whole book is one author’s contribution to precisely that sort of exercise. The Bourget and Chalmers’ paper, however, is quantitative in nature, and despite a number of possible reservations about its methodology (e.g., concerning the sampling protocol, or the fact that the multivariate analyses presented in it are rather preliminary and should really have been much more the focus of attention) it presents an uncommon chance to systematically assess the views of an entire profession. This is the sort of thing that would probably be useful also in other disciplines, from the humanities to the natural sciences, but is all too seldom actually done.

I will focus here on a number of interesting findings that bear directly or indirectly on my overall project of exploring whether and how philosophy makes progress in the conceptual space defined by its own questions and methods. To begin with, is there something to the above mentioned quip, that if there are x philosophers in a room, they are bound to have x+1 opinions (or thereabout) concerning whatever subject matter happens to be under discussion? The data definitely disprove anything like that popular caricature. Consider some of the main findings of the Bourget-Chalmers survey:

71% of respondents thought that a priori knowledge is possible, while only 18% didn’t think so (the remainder, here and in the other cases, falls under the usual heterogeneous category of “other”). There is a clear majority here, despite ongoing discussions on the subject.
However, things are more equally divided when it comes to views on the nature of abstract objects: Platonism gets 39% while nominalism is barely behind, at 38%. Superficially, this may seem an instance of precisely what’s wrong with philosophy, but is in fact perfectly congruent with my model of multiple peaks in conceptual space. Notice that philosophers seem to have settled on two “aporetic clusters,” to use Rescher’s terminology from the Introduction, and have eliminated a number of unacceptable alternatives. There may very well not be an ascertainable fact of the matter about whether Platonism or nominalism is “true.” They are both reasonable ways of thinking about the ontology of abstract objects, with each position subject to further refinement and criticism.
The reader will remember that Quine thought he had demolished once and for all the distinction between analytic and synthetic propositions (one of the famous “two dogmas” of empiricism, see Chapter 3). Well, the bad news for Quine is that about 65% of philosophers disagree, and only 27% agree that such demise has in fact taken place.
One of the most lopsided outcomes of the survey concerns what epistemic attitude is more reasonable to hold about the existence and characteristics of the external world: 82% of respondents qualified themselves as realists, followed by only 5% skeptics and 4% idealists.
Most philosophers are atheists (73%), which, by the way, is a significantly higher percentage than most categories of scientists (Larson and Whitam 1997).
Classical logic, for all the newer developments in that field, still holds sway at 52%, followed by non-classical logic at 15% (though there is a good number of “other” positions being debated, in this case).
Physicalism is dominant in philosophy of mind (57%), while cognitivism seems the way to go concerning moral judgment (66%).
In terms of ethical frameworks, things are much more evenly split, with deontology barely leading at 26%, followed by consequentialism at 24% and virtue ethics at 18%. Here too, as in the case of Platonism vs nominalism, the result makes perfect sense to me, as it is hard to imagine what it would mean to say that deontology, for instance, is the “true” approach to ethics. These three (and a number of others) are reasonable, alternative ways of approaching ethics — and there are a number of unreasonable ones that have been considered and discarded over time.
In philosophy of science, realism beats anti-realism by a large margin, 75% to 12%, which is consistent with my own view that, although anti-realists do have good arguments, the preponderance of considerations clearly favors realism.
And finally (although there are several other entries in the survey worth paying attention to), it turns out that correspondence theories of truth (Chapter 4) win out (51%) over deflationary (25%) and epistemic (7%) accounts.

Bourget and Chalmers then move on to consider the correlations between the answers their colleagues provided to the questions exemplified above and other, possibly influential, factors. Here too, the results are illuminating, and comforting for the profession, I would say. For instance, there was practically no correlation at all between philosophical views and gender, with the glaring (and predictable, and still relatively small) exception of a 0.22 correlation (which corresponds to barely 5% of the variance explained) between gender and one’s views on Philosophy of Gender, Race, and Sexuality. Although the authors report statistically significant correlations between philosophical views and “UK affiliation, continental European nationality, USA PhD, identification with Lewis, and analytic tradition ... [and] ... USA affiliation and nationality, identification with Aristotle and Wittgenstein, and a specialization in Continental Philosophy,” these are all below 0.15 in absolute value, which means we are talking about 2% or less of the variance in the sample. There just doesn’t seem to be much reason to worry that philosophers are characterized by wildly different views depending on their gender, age, or country of origin — as it should be if philosophy is a type of rational inquiry, rather than just a reflection of the cultural idiosyncrasies of its practitioners. The opposite finding would have been somewhat worrisome, though not unknown even in the natural sciences: for instance in the case of Russian vs Western geneticists for most of the 20th century, even independently of the infamous Lisenko affair (Graham 1993).

More interesting are what Bourget and Chalmers call “specialization correlations.” Again, the full article is well worth reading and pondering, but here are some highlights that picked my interest:

Philosophy of religion (a somewhat embattled subfield) is more likely to include people who accept theism and who are libertarian (i.e., reject determinism) in matters of free will. The same people are also (slightly) less likely to embrace physicalism in philosophy of mind, or to accept naturalism as a metaphilosophy. None of this, it should be clear, is at all surprising.
Indeed, most of the strongest correlations between philosophical views and subfields are due to philosophers of religion, with a few others attributable to philosophers of science (who tend to be empiricist rather than rationalists) and scholars interested in ancient philosophy (who tend to adopt virtue ethics rather than deontology or utilitarianism).

Even more fascinating — and congruent with my general thesis in this book — are the pairwise correlations between philosophical views, which hint at the conclusion that philosophers tend to develop fairly internally coherent positions across fields. For instance:

If one thinks that the distinction between analytic and synthetic truths is solid, then one also tends to accept the idea of a priori knowledge — naturally enough.
If a philosopher is a moral realist, she is also likely to be an objectivist about aesthetic value. Interestingly, moral realists also tend to be realists in philosophy of science, and Platonists about abstract objects. It is perfectly sensible to reject moral realism in meta- ethics (44% of philosophers do), but — if one is a moral realist — then one’s reflective equilibrium should consistently lead her to also embrace realism in other areas of philosophy as well, which is exactly what happens according to the data.
If one thinks that Star Trek’s Kirk survives teleportation (rather than being killed and replaced by a copy), one also — coherently — often adopts a psychological view of personal identity.

As one would find in the natural sciences, there are also interesting differences on a given question in the opinions of philosophers who do vs those who do not specialize in the subfield that usually deals with that question. As a scientist, I can certainly have opinions about evolution, climate change and quantum mechanics, but only the first one will be truly informed, since I’m an evolutionary biologist, not an atmospheric or fundamental physicist. So too in philosophy. For instance:

Many more philosophers of science adopt a Humean view of natural laws when compared to average philosophers from other disciplines.
More metaphysicians are Platonists, though that particular differential is not very high (15%).
More epistemologists accept a correspondence theory of truth (again, however, the differential is not high: 12%).

Bourget and Chalmers even explored the relationship between one’s identification with a major philosophical figure and one’s views about certain topics. The results are consistent and not surprising, again demonstrating that philosophy is not the Wild West of intellectual inquiries:

If a philosopher admires Quine, he is less likely to accept the analytic-synthetic distinction (and more likely to reject the possibility of a priori knowledge).
Someone who finds kinship with Aristotle is also probably a virtue ethicist.
In political philosophy, if John Rawls is your guy, you are less likely to be a communitarian.
And it really ought not to be surprising at all that philosophers who like Plato are, well, Platonists about abstract objects.

Once more: looking at this data and asking “yes, yes, but which one is the true view of things?” is missing the point entirely.

Perhaps the most interesting and nuanced approach that Bourget and Chalmers take to their data unfolds when they move from uni- and bi-variate to multi-variate statistics, in this case factor and principal components analyses. This allows them to examine the many-to-many relationships among variables in their data set. The first principal component they identify, i.e., the one that explains most of the variance in the sample, they label “Anti-naturalism,” as it groups a number of responses that coherently fall under that position: libertarianism concerning free will, non-physicalism about the mind, theism, non-naturalism as a metaphilosophy, metaphysical possibility of p-zombies, and so-called “further fact” view of personal identity. If one were to plot individual responses along this dimension (which Bourget and Chalmers don’t do, unfortunately), one would see anti- naturalist philosophers clustering at the positive end of it, and naturalist philosophers clustering at the negative end. It would be interesting to see the actual scatter of data points, to get a better sense of the variation in the sample.

The second-ranked principal component is labeled “Objectivism / Platonism” by the authors, and features positive loadings (i.e., multivariate correlations) of cognitivism in moral judgment, realism in meta-ethics, objectivism about aesthetic value, and of course Platonism about abstract objects. The third component is about Rationalism, with positive loadings for the possibility of a priori knowledge, the analytic-synthetic distinction, and rationalism about knowledge. Two more interesting components (ranked fourth and fifth respectively) concern “Anti-realism” (epistemic conception of truth, anti-realism about scientific theories, idealism or skepticism about the external world, Humean conception of laws of nature, and a Fregean take on proper names) and “Externalism” (externalism about mental content, epistemic justification, and moral motivation, as well as disjunctivism concerning perceptual experience). Finally we get two additional components that summarize a scatter of other positions.

The overall picture that emerges, again, is very much that of a conceptual landscape with a number of alternative peaks, which are internally coherent and well refined by centuries of philosophical inquiry. I suspect that historically many more “peaks” have been explored and eventually discarded, and that the height of the current peaks (as reflected by the consensus gathered within the relevant epistemic communities) is itself heterogeneous and dynamic, with some in the process of becoming more prominent in the landscape and others on their way to secondary status or destined to disappear altogether.

The evolution of philosophy

It has been a long excursion across the intellectual landscapes that characterize the general practice that goes under the name of “philosophy,” a practice that has been carried out in many forms throughout the world across millennia. I have put forth the proposition that, broadly speaking and with a number of caveats and exceptions, what we call “philosophy” hangs in a series of empirically informed conceptual spaces. At times, it has a tendency to veer too far from empirical background (both folk and science-based), in which case it begins to lose relevance, and sometimes it even manages to look somewhat silly. The chief reason, I maintain, is that logical constraints are simply too broad, not “constraining” enough: logic is compatible with too many possibilities, and logical coherence is necessary but not sufficient for good philosophy. One needs a science-informed and science-compatible (though certainly not science-deferring) philosophy.

So, does philosophy, construed in the way suggested above, make progress? I think it does, in the sense of exploring and refining the sort of conceptual spaces that I have tried to describe especially in Chapter 6, and in a way that lies somewhere between science (Chapter 4) and mathematics and logic (Chapter 5), but closer to the latter two. As for the future of the discipline — qua form of intellectual inquiry, and quite aside from the politics of academia — I am optimistic, as I see it rather bright. So long as there will be people interested in thoughtful, critical assessments of broad swaths of what counts as human understanding, there will be philosophy, its current loud scientistic detractors (Chapter 1) notwithstanding.

Often philosophers themselves have advanced a model of their discipline as a “placeholder” for the development of eventually independent fields of inquiry, presenting philosophy as the business of conducting the initial conceptual exploration (and, hopefully, clarification) of a given problem or set of problems, handing it then to a special science as soon as that problem becomes empirically tractable. There are quite a few historical examples to back up this view, from the emergence of the natural sciences to that of psychology and linguistics, to mention a few. Philosophy of mind is arguably currently in the midst of this very process, interfacing with the nascent cognitive sciences.

Predictably, this very same model is often twisted by detractors of philosophy to show that the field has been in a slow process of disintegrating itself, with a hard core (represented by metaphysics, ethics, epistemology, logic, aesthetics, and the like) that is the last holdout, and which has shown increasing signs of itself yielding to the triumphal march of Science (with a capital “S”). If that is the case, of course, so be it. But I seriously doubt it. What we have seen over the last few centuries, and especially the last one or so, is simply a transformation of what it means to do philosophy, a transformation that I think is part of the continuous rejuvenation of the field. This should be neither surprising nor assumed to be unique to philosophy. Although we use the general word “science” to indicate — depending on whom one asks — everything from Aristotle’s forays into biology to what modern physicists are doing with the Large Hadron Collider, the very nature of science has evolved throughout the centuries, and keeps evolving still. What counts as good scientific methodology, sound scientific theorizing, or interesting scientific problems has changed dramatically from Aristotle to Bacon to Darwin to Stephen Hawking. Why should it be any different for philosophy?

One of the most obvious indications that philosophy has been reinventing itself over the past century or so is the dramatic onset of a panoply of “philosophies of.” While — bizarrely — I know a number of colleagues who think that philosophy of science, or philosophy of language, or any other philosophy of X barely qualify as philosophy, one can argue that the majority of the modern philosophical literature falls into those areas, rather than the core ones enumerated above. “Philosophies of” are the way the field has been responding to the progressive emancipation of some of its former branches: science is no longer natural philosophy, but that simply means that now philosophers are free to philosophize about science (and, more specifically, about biology, quantum mechanics, etc.) without having to actually do science. The same idea applies to linguistics (and philosophy of language), psychology (and philosophy of the social sciences), economics (and philosophy of economics), and so on and so forth.

Is this sort of transformation also about to affect philosophy’s core areas of metaphysics, ethics, epistemology, logic and aesthetics? It depends on how one looks at things. On the one hand, to a larger or lesser extent it certainly has become increasingly difficult to engage in any of the above without also taking on board results from the natural and social sciences. While logic is perhaps the most shielded of all core philosophical areas in this respect (indeed, it has contributed to the sciences broadly construed significantly more than it has received), it is certainly a good idea to do metaphysics while knowing something about physics (and biology); ethics while interfacing with political and social sciences, and even biology and neuroscience; epistemology while being aware of the findings of the cognitive sciences; and aesthetics with an eye toward biology and social science. Nonetheless, all the core areas of philosophy are still very much recognizable as philosophy, and will likely remain so for quite some time. But should they finally spawn their own independent disciplines, then there will immediately arise in turn a need for more “philosophies of,” and the process will keep continuing, the field adapting and regenerating.

Ultimately, philosophy is here to stay for the same reason that other humanities (and the arts) will stay, regardless of how much science improves and expands, or how much narrow minded politicians and administrators will keep cutting their funding in universities: human beings need more than facts and formulas, more than experiment and observation. They need to experience in the first person, and they need to critically reflect on all aspects of their existence. They need to understand, in the broadest possible terms, which means they need to philosophize.

Literature Cited

Adams, M.B. (ed.) (1990) The Wellborn Science: Eugenics in Germany, France, Brazil, and Russia. Oxford University Press.

Aiden, E. and Michel, J-P. (2013) Uncharted: Big Data as a Lens on Human Culture. Riverhead Hardcover.

Albert, D. (2012) On the origin of everything. The New York Times, 23 March.

Alexander, J. (2012) Experimental Philosophy: An Introduction. Polity Press.

Andersen, R. (2013) Has physics made philosophy and religion obsolete? The Atlantic, 23 April.

Anderson, P.W. (1972) More is different. Science, 177:393-396.

Antony, L.M. (2001) Quine as feminist: the radical import of naturalized epistemology. In: L.M. Antony and C.E. Witt (eds.) A Mind of One's Own: Feminist Essays on Reason and Objectivity. Westview Press, pp. 110-153.

Ariew, R. (1984) The Duhem thesis. British Journal for the Philosophy of Science 35:313-325.

Aristotle (350 BCE) Metaphysics (translated by W.D. Ross) (accessed on 31 May 2013).

Asenjo, F.G. (1966) A Calculus of Antinomies. Notre Dame Journal of Formal Logic 7:103-105.

Baggini, J. and Krauss, L. (2012) Philosophy vs science: which can answer the big question of life? The Guardian, 9 September.

Baggott, J. (2013) Farewell to Reality: How Modern Physics Has Betrayed the Search for Scientific Truth. Pegasus.

Bailin, D. and Love, A. (2010) Supersymmetric Gauge Field Theory and String Theory. CRC Press.

Balaguer, M. (1998) Platonism and Anti-Platonism in Mathematics. Oxford University Press.

Bartels, D.M. and Pizarro, D.A. (2011) The mismeasure of morals: antisocial personality traits predict utilitarian responses to moral dilemmas. Cognition 121:154-161.

Bashmakova, I.G. (1956) Differential methods in Archimedes’ works. In: Actes du VIII Congres Internationale d’Histoire des Sciences. Vinci: Gruppo Italiano di Storia delle Scienze, pp. 120-122.

Bealer, G. (1998) Intuition and the Autonomy of Philosophy. In: M. DePaul and W. Ramsey (eds.), Rethinking Intuition: The Psychology of Intuition and Its Role in Philosophical Inquiry. Rowman & Littlefield, Lanham, pp. 201–240.

Beall, J.C. (ed.) (2003) Liars and Heaps. Clarendon Press.

Beany, M. (2009) Analysis. Stanford Encyclopedia of Philosophy (accessed on 28 August 2014).

Bell, E.T. (1945) The Development of Mathematics. McGraw-Hill.

Benacerraf, P. (1973) Mathematical truth. The Journal of Philosophy 70:661-679.

Bentham, J. (1978). Offences Against Oneself. L. Compton (ed.), The Journal of Homosexuality 3:389-406 and 4:91-107.

Benthem, J.F. van (1983) Modal Logic and Classical Logic Bibliopolis.

Benzon, B. (2014) The only game in town: digital criticism comes of age. 3quarksdaily, 5 May 2014 (accessed on 27 August 2014).

Bergrren, J.L. (1984) History of Greek mathematics: a survey of recent research. Historia Mathematica 11:394-410.

Berman, B. (2015) A science of literature. Boston Review, 3 August 2015.

Berry, S. (2010) Is math logic? (accessed on 16 April 2016).

Bigelow, J. (1988) The Reality of Numbers: A Physicalist's Philosophy of Mathematics. Clarendon.

Bird, A. (2007) What is scientific progress? Nous 41:64-89.

Bird, A. (2010) The epistemology of science — a bird’s eye view. Synthese DOI 10.1007/s11229-010-9740-4.

Bird, O. (1963) The history of logic. The Review of Metaphysics 16:491-502.

Blackburn, S. and Simmons, K. (eds.) (1999) Truth. Oxford University Press.

Block, N. and Kitcher, P. (2010) Misunderstanding Darwin. Boston Review, March/April.

Bobzien, S. (2006) Ancient logic. Stanford Encyclopedia of Philosophy (accessed on 2 August 2013).

Bogaard, P.A. (1978) The limitations of physics as a chemical reducing agent. Proceedings of the Philosophy of Science Association 2:345–356.

BonJour, L. (1999) The Dialectic of Foundationalism and Coherentism. In J. Greco and E. Sosa (eds.), The Blackwell Guide to Epistemology. Blackwell, pp. 117–142.

Bordogna, F. (2008) William James at the Boundaries: Philosophy, Science, and the Geography of Knowledge. University of Chicago Press.

Boudry, M. (2013) Loki’s Wager and Laudan’s Error. On Genuine and Territorial Demarcation. In: M. Pigliucci and M. Boudry, The Philosophy of Pseudoscience: Reconsidering the Demarcation Problem. University of Chicago Press, 79-98.

Bourget, D. and Chalmers, D.J. (2013) What do philosophers believe? Philosophical Studies 3:1-36.

Bowler, P.J. and Morus, I.R. (2005) Making Modern Science: A Historical Survey. University Of Chicago Press.

Boyd, R. (1973) Realism, underdetermination, and a causal theory of evidence. Nois 7:1-12.

Boyd, R. (2007) What Realism implies and what it does not. Dialectica 43:5-29.

Brigandt, I. (2003) Species Pluralism Does Not Imply Species Eliminativism. Philosophy of Science 70:1305–1316.

Brown, B. (2002) On Paraconsistency. In: D. Jacquette (ed.), A Companion to Philosophical Logic, Blackwell, pp. 628-650.

Brown, J.R. (1991). The laboratory of the mind: Thought experiments in the natural sciences. Routledge.

Brown, J.R. (2002) Thought experiments. Stanford Encyclopedia of Philosophy (accessed on 11 September 2014).

Brown, J.R. (2008) Philosophy of Mathematics: A Contemporary Introduction to the World of Proofs and Pictures. Routledge.

Brown, J.R. (ed.) (2012) Philosophy of Science: The Key Thinkers. Continuum.

Bueno, O. (2013) Nominalism in the philosophy of mathematics. Stanford Encyclopedia of Philosophy (accessed on 11 June 2015).

Burdick, A., Drucker, J., Lunenfeld, P., Presner, T., and Schnapp, A (2012) Digital_Humanities. MIT Press.

Cameron, P. (2010) Mathematics and logic (accessed on 10 August 2015).

Campbell, R. (2011) Moral epistemology. Stanford Encyclopedia of Philosophy (accessed on 11 October 2012).

Cappelen, H. (2012) Philosophy Without Intuitions. Oxford University Press.

Carroll, S. (2013) Mind and Cosmos. Preposterous Universe, 22 August.

Carnap, R. (1937) The Logical Syntax of Language. Kegan Paul, Trench, Trubner & Co.

Cartwright, N. (1983) How the Laws of Physics Lie. Oxford University Press.

Casadevall, A. (2015) Put the “Ph” Back in PhD. Johns Hopkins Public Health, Summer 2015.

Caverni, J.-P., Fabre, J.-M., and Gonzalez, M. (1990) Cognitive Biases. Elsevier Science.

Chakravartty, A. (2003) The Structuralist Conception of Objects. Philosophy of Science 70:867–878.

Chakravartty, A. (2004) Structuralism as a Form of Scientific Realism. International Studies in Philosophy of Science 18:151–171.

Chakravartty, A. (2011) Scientific Realism. Stanford Encyclopedia of Philosophy (accessed on 26 June 2012).

Chalmers, A.F. (2013) What Is This Thing Called Science? Hackett Publishing.

Chalmers, D. (2015) Why Isn’t There More Progress in Philosophy? Philosophy 90:3-31.

Chalmers, D., Manley, D. and Wassermann, R. (eds.) (2009) Metametaphysics: New Essays on the Foundations of Ontology. Oxford University Press.

Chang, R. (1997) Incommensurability, Incomparability, and Practical Reason. Harvard University Press.

Chappell, S.G. (2013) Plato on Knowledge in the Theaetetus. Stanford Encyclopedia of Philosophy (accessed on 18 June 2015).

Charness, N. (1991) Expertise in chess: the balance between knowledge and search. In: K. Anders Ericsson and J. Smith (eds.) Toward a General Theory of Expertise: Prospects and Limits. Cambridge University Press.

Chase, J.M. (2011) Ecological niche theory. In: S.M. Scheiner and M.R. Willig (eds.) The Theory of Ecology, University of Chicago Press.

Churchland, P. (1985) The ontological status of observables: in praise of the superempirical virtues.” In: P. Churchland and C. Hooker (eds.), Images of Science: Essays on Realism and Empiricism, University of Chicago Press, pp. 35–47.

Clatterbuck, H. (2013) The epistemology of thought experiments: A non-eliminativist, non-Platonic account. European Journal for Philosophy of Science 3:309-329.

Collins, H. (1981) Stages in the Empirical Programme of Relativism. Social Studies of Science 11:3-10.

Colyvan, M. (2012) An Introduction to the Philosophy of Mathematics. Cambridge University Press.

Conee, E. and Feldman, R. (1985) Evidentialism. Philosophical Studies 48:15–35.

Cooke, R.L. (2011) The History of Mathematics: A Brief Course. John Wiley & Sons.

Cooper, D.E. (1994) Analytical and continental philosophy. Proceedings of the Aristotelian Society 94:1-18.

Copeland, B.J. (2002) The genesis of possible worlds semantics. Journal of Philosophical Logic 31:99-137.

Coyne, J. (2010) The improbability pump. The Nation, 22 April.

Crowe, M.J. (1975) Ten ‘laws’ concerning patterns of change in the history of mathematics. Historia Mathematica 2:161-166.

Crowe, M.J. (1988) Ten misconceptions about mathematics and its history. In: W. Asprey and P. Kiteher (eds.), History and Philosophy of Modern Mathematics, Minnesota Studies in the Philosophy of Science, Vol. XI, University of Minnesota Press, pp. 260-277.

Daniels, N. (2003) Reflective equilibrium. Stanford Encyclopedia of Philosophy (accessed on 11 September 2014).

David, M. (2009) The Correspondence Theory of Truth. Stanford Encyclopedia of Philosophy (accessed on 8 May 2013).

Davis, B.W. (2010) The Kyoto School. Stanford Encyclopedia of Philosophy (accessed on 19 July 2012).

Dennett, D. (1996) Darwin’s Dangerous Idea: Evolution and the Meanings of Life. Simon & Schuster.

Dennett, D. (2014) Intuition Pumps And Other Tools for Thinking. W. W. Norton.

DePaul, M. (ed.) (2001) Resurrecting Old-Fashioned Foundationalism. Rowman and Littlefield.

DeRose, K., and Warfield, T. (1999) Skepticism. A Contemporary Reader. Oxford University Press.

Descartes, R. (1637 / 2000) Discourse on Method and Related Writings. Penguin Classics.

Descartes, R. (1639 / 1991) Letter to Mersenne: 16 October 1639. In: The Philosophical Writings of Descartes, Vol. 3. Cambridge University Press.

Descartes, R. (1684) Rules for the Direction of the Mind (accessed on 28 August 2014).

Devitt, M. (2011) Are unconceived alternatives a problem for scientific realism? Journal for General Philosophy of Science 42:285-293.

Dietrich, E. (2011) There is no progress in philosophy. Essays in Philosophy 12:329-344.

Dretske, Fred. 1970. Epistemic Operators. The Journal of Philosophy 67:1007– 1023.

Driver, J. (2009) The history of utilitarianism. Stanford Encyclopedia of Philosophy (accessed on 26 June 2012).

Dummett, M. (1978) Can analytical philosophy be systematic, and ought it to be? In: Truth and Other Enigmas. Duckworth.

Dupré, J. (1993) The Disorder of Things: Metaphysical Foundations of the Disunity of Science. Harvard University Press.

Dupré, J. (2012) Mind and Cosmos. Notre Dame Philosophical Reviews, 29 October.

Dutilh-Novaes, C. (2008) Logic in the 14th Century after Ockham. In: D. Gabbay and J. Woods (eds.), Handbook of the History of Logic, vol. 2, Medieval and Renaissance Logic, North Holland.

Edmonds, D. and Eidinow, J. (2001) Wittgenstein's Poker: The Story of a Ten-Minute Argument Between Two Great Philosophers. Ecco.

Einstein, A. (1920) Relativity: The Special and General Theory. Chapter XXXI (accessed on 22 November 2015).

Ereshefsky, M. (1998) Species Pluralism and Anti-Realism. Philosophy of Science 65:103–120.

Feyerabend, P. (1974) How to defend society against science (accessed on 7 August 2012).

Feyerabend, P. (1975) Against Method. Verso.

Field, H. (1972) Tarski’s theory of truth. The Journal of Philosophy 69:347-375.

Fisher, A. (2011) Metaethics: An Introduction. Acumen Publishing.

Fodor, J. (1974) Special sciences (Or: the disunity of science as a working hypothesis). Synthese 28:97-115.

Fodor, J. (2000) The Mind Doesn't Work That Way. MIT Press.

Fodor, J. and Piattelli-Palmarini, M. (2010) What Darwin Got Wrong. Farrar, Strauss & Giroux.

Fogelin, R.J. (1997) Quine’s limited naturalism. The Journal of Philosophy 94:543-563. Foucault, M. (1961 / 2006) History of Madness. Routledge.

Frigg, R. and Votsis, I. (2011) Everything you always wanted to know about structural realism but were afraid to ask. European Journal for Philosophy of Science 1:227-276.

Fumerton, R. (2010) Foundationalist theories of epistemic justification. Stanford Encyclopedia of Philosophy (accessed on 7 August 2012).

Ganeri, J. (ed.) (2001) Indian Logic: A Reader. Curzon.

Garson, J. (2009) Modal Logic. Stanford Encyclopedia of Philosophy (accessed on 31 May 2013).

Gettier, E.L. (1963) Is justified true belief knowledge? Analysis 23:121-123.

Giere, R. (1988) Explaining Science: A Cognitive Approach. University of Chicago Press. Giere, R. (2010) Scientific Perspectivism. University of Chicago Press.

Giles, J. (2005) Internet encyclopaedias go head to head. Nature 438:900-901.

Gill, M. (2000) Hume’s Progressive View of Human Nature. Hume Studies 26:87-108.

Gillon, Brendan S. (ed.) (2010) Logic in earliest classical India. Motilal Banarsidass Publishers, pp. 167-182.

Gillon, B. (2011) Logic in classical Indian philosophy. Stanford Encyclopedia of Philosophy (accessed on 20 July 2012).

Gobet, F. and Simon, H.A. (1996) The role of recognition processes and look-ahead search in time-constrained expert problem solving: evidence from Grand-Master-level chess. Psychological Science 7:52-55.

Godfrey-Smith, P. (2006) The strategy of model-based science. Biology & Philosophy 21:725–40.

Godfrey-Smith, P. (2010) It got eaten. London Review of Books, 8 July.

Godfrey-Smith, P. (2013) Not sufficiently reassuring. London Review of Books, 24 January.

Goldman, A. (2007) Philosophical intuitions: their target, their source, and their epistemic status. Grazer Philosophische Studien 74:1-26.

Goldman, R. (2011) Understanding quaternions. Graphical Models 73:21-49.

Goodman, N. (1955) Fact, Fiction, and Forecast. Harvard University Press.

Gottwald, S. (2009) Many-valued logic. Stanford Encyclopedia of Philosophy (accessed on 22 August 2013).

Gould, S.J. and Lewontin, R.C. (1979) The spandrels of San Marco and the Panglossian paradigm: a critique of the adaptationist program. Proceedings of the Royal Society of London, B205:581-598.

Goulet, R. (2013) Ancient philosophers: a first statistical survey. In: M. Chase, S.R.L. Clarke, and M. McGhee (eds.) Philosophy as a Way of Life: Ancients and Moderns — Essays in Honor of Pierre Hadot. John Wiley & Sons.

Graham, L.R. (1993) Science in Russia and the Soviet Union: A Short History. Cambridge University Press.

Graham, M.H. and Dayton, P.K. (2002) On the evolution of ecological ideas: paradigms and scientific progress. Ecology 83:1481-1489.

Grattan-Guiness, I. (2004) The mathematics of the past: distinguishing its history from our heritage. Historia Mathematica 31:163-185.

Greco, J. (1999) Agent Reliabilism. Philosophical Perspectives 19:273–96.

Griffith, M. (2013) Free Will: The Basics. Routledge.

Hacking, I. (1983) Representing and Intervening: Introductory Topics in the Philosophy of Natural Science. Cambridge University Press.

Haidt, J. (2012) The Righteous Mind: Why Good People Are Divided by Politics and Religion. Pantheon.

Hajek, P. (2010) Fuzzy logic. Stanford Encyclopedia of Philosophy (accessed on 30 March 2011).

Hansson, S.O. (2012) Editorial: Progress in Philosophy? A Dialogue. Theoria 78:181-185.

Harding, S. (1989) Value-free research is a delusion. New York Times, 22 October.

Harding, S. (ed.) (2004) The Feminist Standpoint Reader. Routledge.

Hare, R.M. (1973) Rawls’ Theory of Justice. Philosophical Quarterly 23:144-155; 241-251.

Harris, S. (2011) The Moral Landscape: How Science Can Determine Human Values. Free Press.

Heisig, J.W. (2001) Philosophers of Nothingness: An Essay on the Kyoto School. University of Hawaii Press.

Hempel, C.G. (1945/1953) Geometry and Empirical Science. In: P.P. Weiner (ed.), Readings in the Philosophy of Science, Appleton-Century-Crofts.

Hempel, C.G. (1966) Philosophy of Natural Science. Prentice-Hall.

Henson, R.K. and Smith, A.D. (2000) State of the art in statistical significance and effect size reporting: A review of the APA Task Force report and current trends. Journal of Research & Development in Education 33:285-296.

Hesse, M. (1974) The Structure of Scientific Inference. University of California Press.

Hesse, M. (1980) Revolutions and Reconstructions in the Philosophy of Science. Indiana University Press.

Hilpinen, R. (1971) Deontic Logic: Introductory and Systematic Readings D. Reidel.

Hodgkinson, G.P., Langan-Fox, J. and Sadler-Smith, E. (2008) Intuition: a fundamental bridging construct in the behavioural sciences. British Journal of Psychology 99:1-27.

Hookway, C. (2008) Pragmatism. Stanford Encyclopedia of Philosophy (accessed on 4 June 2013).

Horgan, J. (1996) The End Of Science: Facing The Limits Of Knowledge In The Twilight Of The Scientific Age. Basic Books.

Horwich, P. (1990) Truth. Blackwell.

Hutcheson, F. (1738) An Inquiry Concerning Moral Good and Evil. Full text at the University of Toronto Robarts Library (accessed on 7 May 2014).

Hylton, P. (2010) Willard van Orman Quine. Stanford Encyclopedia of Philosophy (accessed on 19 December 2012).

Hume, D. (1739-40) A Treaty of Human Nature (accessed on 24 August 2012).

Hume, D. (1748) An Enquiry Concerning Human Understanding (accessed on 8 February 2013).

Inwood, B. (editor) (2003) The Cambridge Companion to the Stoics. Cambridge University Press.

Irvine, A.D. (2009) Philosophy of Mathematics. North Holland.

James, W. (1907 / 1975) Pragmatism: A New Name for some Old Ways of Thinking. Harvard University Press.

Joll, N. (2010) Contemporary metaphilosophy. Internet Encyclopedia of Philosophy (accessed on 26 June 2012).

Joravsky, D. (1970) The Lysenko Affair. University of Chicago Press.

Kadane, J.B. (2011) Bayesian Methods and Ethics in a Clinical Trial Design. John Wiley & Sons.

Kahane, G., Everett, J.A.C., Earp, B.D., Farias, M. and Savulescu, J. (2015) ‘Utilitarian’ judgments in sacrificial moral dilemmas do not reflect impartial concern for the greater good. Cognition 134:193–209.

Kahneman, D. (2011) Thinking, Fast and Slow. Farrar, Straus and Giroux.

Kaiser, M.I. and Seide, A. (2013) Philip Kitcher: Pragmatic Naturalism. Walter de Gruyter.

Kaplan, J.M. (2000) The Limits and Lies of Human Genetic Research: Dangers For Social Policy. Routledge.

Kapp, E., (1942) Greek Foundations of Traditional Logic. Columbia University Press. Keller, E.F. (1983) A Feeling for the Organism: The Life and Work of Barbara McClintock. W.H. Freeman.

Kekes, J. (1980) The Nature of Philosophy. Rowman and Littlefield.

Kinchin, I.M. (2014) Concept Mapping as a Learning Tool in Higher Education: A Critical Analysis of Recent Reviews. The Journal of Continuing Higher Education 62:39-49.

King, P. and Shapiro, S. (1995) The history of logic. In: T. Honderich (ed.), The Oxford Companion of Philosophy, Oxford University Press, pp. 496-500.

Kirsch, A (2014) Technology is taking over English departments. New Republic (access on 27 August 2014).

Kitcher, P. (1980) Mathematical Rigor—Who Needs It? Nous 15: 490.

Kitcher, P. (1985) The Nature of Mathematical Knowledge. Oxford University Press. Kitcher, P. (1993) The Advancement of Science: Science Without Legend, Objectivity Without Illusions. Oxford University Press.

Kitcher, P. (2012) Preludes to Pragmatism: Toward a Reconstruction of Philosophy. Oxford University Press.

Kline, R.B. (2011) Principles and Practice of Structural Equation Modeling. Guilford Press.

Kneale, M. and Kneale, W. (1962) The Development of Logic. Clarendon Press.

Knobe, J., Buckwalter, W., Nichols, S., Robbins, P., Sarkissian, H. and Sommers, T. (2012) Experimental Philosophy. Annual Review of Psychology 63:81-99.

Kornblith, H. (2001) Epistemology: Internalism and Externalism. Blackwell.

Kuntz, J.R. and Kuntz, J.R.C. (2011) Surveying Philosophers About Philosophical Intuition. Review of Philosophy and Psychology 2:643-665.

Krantz, S.G. (2010) An Episodic History of Mathematics: Mathematical Culture Through Problem Solving. MAA.

Krauss, L.M. (2012) The consolation of philosophy. Scientific American, 27 April.

Kretzmann, N. et al. (eds.) (1982) The Cambridge History of Later Medieval Philosophy: From the Rediscovery of Aristotle to the Disintegration of Scholasticism, 1100–1600. Cambridge University Press.

Kripke, S.A. (1980) Naming and Necessity. Blackwell.

Krips, H. (1990) The Metaphysics of Quantum Theory. Clarendon.

Kuhn, T. (1963) The Structure of Scientific Revolutions. University of Chicago Press.

Kuhn, T. (1982) Commensurability, comparability, communicability. Philosophy of Science 2:669-688.

Kuhn, T. (2012) The Structure of Scientific Revolutions: 50th Anniversary Edition. University of Chicago Press.

Labinger, J.A. and Collins, H. (eds.) (2001) The One Culture?: A Conversation about Science. University Of Chicago Press.

Ladyman, J. (1998) What is structural realism? Studies in History and Philosophy of Science 29:409–424.

Ladyman, J. (2009) Structural Realism. Stanford Encyclopedia of Philosophy (accessed on 16 August 2012).

Ladyman, J. (2012) Understanding Philosophy of Science. Routledge.

Ladyman, J. and Ross, D. (2009) Every Thing Must Go: Metaphysics Naturalized. Oxford University Press.

Lagerlund, H. (2000). Modal Syllogistics in the Middle Ages. Brill.

Lagerlund, H. (2010) Medieval theories of the syllogism. Stanford Encyclopedia of Philosophy (accessed on 2 August 2013).

Lakatos, I. (1963/64) Proofs and refutations. British Journal for the Philosophy of Science 14:1-25, 120-139, 221-243, 296-342.

Lakatos, I. (1970) Falsification and the methodology of scientific research programs. In: Criticism and the Growth of Knowledge, I. Lakatos and A. Musgrave (eds.), Cambridge University Press, pp. 170-196.

Lakatos, I. (1978) Infinite Regress and the Foundations of Mathematics, A Renaissance of Empiricism in Recent Philosophy of Mathematics, and Cauchy and the Continuum: The Significance of the Non-Standard Analysis for the History and Philosophy of Mathematics. In: J. Worrall and G. Currie (eds.) Lakatos’s Mathematics, Science and Epistemology. Philosophical Papers, Cambridge University Press.

Larson, E.J. and Whitam, L. (1997) Scientists are still keeping the faith. Nature 386:435-436.

Latour, B. (1988) A relativistic account of Einstein’s relativity. Social Studies of Science 18:3-44.

Latour, B. and Woolgar, S. (1986) Laboratory Life: The Construction of Scientific Facts. Princeton University Press.

Laudan, L. (1981a) A problem-solving approach to scientific progress. In: Ian Hacking (ed.), Scientific Revolutions. Oxford University Press.

Laudan, L. (1981b) A Confutation of Convergent Realism. Philosophy of Science 48:19– 48.

Laudan, L. (1983). The demise of the demarcation problem. In: R.S. Cohan and L. Laudan (eds.) Physics, Philosophy, and Psychoanalysis. Reidel.

Laudan, L. (1990) Normative naturalism. Philosophy of Science 57:44-59.

Lawton, J.H. (1999) Are There General Laws in Ecology? Oikos 84:177-192.

Lear, J. (1980) Aristotle and Logical Theory. Cambridge University Press.

Leiter, B. and Weisberg, M. (2012) Do You Only Have a Brain? On Thomas Nagel. The Nation, 3 October.

Lemmon, E. and Scott, D. (1977) An Introduction to Modal Logic. Blackwell.

Lennox, J. (2011) Aristotle’s biology. Stanford Encyclopedia of Philosophy (accessed on 27 August 2014).

Levy, N. (2003) Analytic and continental philosophy: explaining the differences. Metaphilosophy 34:284-304.

Lewontin, R.C. (2010) Not so natural selection. The New York Review of Books, 27 May.

Lindberg, D.C. (2008) The Beginnings of Western Science: The European Scientific Tradition in Philosophical, Religious, and Institutional Context, Prehistory to A.D. 1450. University Of Chicago Press.

Linnebo, Ø. (2011) Platonism in the philosophy of mathematics. Stanford Encyclopedia of Philosophy (accessed on 11 October 2012).

Lipton, P. (2004) Inference to the Best Explanation. Psychology Press.

Littlejohn, R. (2005) Comparative philosophy. Internet Encyclopedia of Philosophy (accessed on 19 July 2012).

Longino, H. (1990) Science as Social Knowledge: Values and Objectivity in Scientific Inquiry. Princeton University Press.

Longino, H. (2006) The social dimensions of scientific knowledge. Stanford Encyclopedia of Philosophy (accessed on 25 July 2012).

Love, A. (2009) Marine invertebrates, model organisms, and the modern synthesis: epistemic values, evo-devo, and exclusion. Theory in Bioscience 128:19–42.

Love, A. (2013) Experiments, Intuitions and Images of Philosophy and Science. Analysis Reviews 73:785-797.

Lynch, M. (2007) The frailty of adaptive hypotheses for the origins of organismal complexity. Proceedings of the National Academy of Sciences, USA. 104:8597-8604.

Machery, E., S. Stich, D. Rose, et al. (2015) Gettier across cultures. Noûs, online 13 August 2015, DOI: 10.1111/nous.12110.

Maddy, P. (1990) Realism in Mathematics. Clarendon.

Maffie, J. (1995) Scientism and the independence of epistemology. Erkenntnis 43:1-27.

Mahoney, M.S. (1968) Another look at Greek geometric analysis. Archive for History of Exact Sciences 5:318-348.

Marche, S. (2012) Literature is not Data: Against Digital Humanities. LA Review of Books (accessed on 27 August 2014).

Mares, E.D. (1997) Relevant Logic and the Theory of Information. Synthese 109:345–360.

Mares, E. (2012) Relevance logic. Stanford Encyclopedia of Philosophy (accessed on 28 August 2013).

Matilal, B.K. (1998) The Character of Indian Logic. State University of New York Press.

Maxwell, G. (1972) Scientific methodology and the causal theory of perception. In: H. Feigl, H. Sellars and K. Lehrer (eds.), New Readings in Philosophical Analysis. Appleton-Century Crofts, pp. 148–177.

McGinn, C. (1993) Problems in Philosophy: The Limits of Inquiry. Blackwell.

McNamara, P. (2010) Deontic logic. Stanford Encyclopedia of Philosophy (accessed on 22 August 2013).

Mehrtens, H. (1976) T.S. Kuhn’s theories and mathematics: a discussion paper on the ‘new historiography’ of mathematics. Historia Mathematica 3:297-320.

Merriman, B. (2015) A Science of Literature, Boston Review, 3 August (accessed on 9 May 2016).

Meyer, A. (2011) On the Nature of Scientific Progress: Anarchistic Theory Says ‘Anything Goes’ — But I Don't Think So. PLoS Biology 9:e1001165.

Mill, J.S. (1861) Utilitarianism. R. Crisp (ed.), Oxford University Press, 1998.

Mill, J.S. (1874) A System of Logic, Ratiocinative and Inductive: Being a Connected View of the Principles of Evidence and the Methods of Scientific Investigation. Harper & Row.

Mishler, B.D. and Donoghue, M.J. (1982) Species concepts: a case for pluralism. Systematic Zoology 31:491-503.

Monton, B. and Mohler, C. (2008) Constructive Empiricism. Stanford Encyclopedia of Philosophy (accessed on 26 June 2012).

Moody, T.C. (2006) Progress in philosophy. American Philosophical Quarterly 23:35-46.

Moon, B.M., Hoffman, R.R., Novak, J.D. and Cañas, A.J. (2011) Applied Concept Mapping: Capturing, Analyzing, and Organizing Knowledge. CRC Press.

Moore, G.E. (1959) Philosophical Papers. Allen and Unwin.

Moretti, F. (2009) Style, Inc. Reflections on Seven Thousand Titles (British Novels, 1740–1850), Critical Inquiry 36:134-158.

Moschovakis, J. (2010) Intuitionistic logic. Stanford Encyclopedia of Philosophy (accessed on 22 August 2013).

Müller, G.B. and Newman, S.A. (2005) The innovation triad an EvoDevo agenda. Journal of Experimental Zoology 304B:487–503.

Mulligan, K., Simons, P. and Smith, B. (2006) What’s wrong with contemporary philosophy? Topoi 25:63-67.

Naes, A. and Hanay, A. (1972) Invitation to Chinese Philosophy: Eight Studies. Universitetsforlaget.

Nagel, E. (1955) Naturalism reconsidered. Proceedings of the American Philosophical Association 28:5-17.

Nagel, T. (1974) What is it like to be a bat? The Philosophical Review 83:435-450.

Nagel, T. (1986) The View From Nowhere. Oxford University Press.

Nagel, T. (2012) Mind and Cosmos. Oxford University Press.

Nakagawa, S. and Cuthill, I.C. (2007) Effect size, confidence interval and statistical significance: a practical guide for biologists. Biological Reviews 82:591–605.

Neurath, O., Carnap, R., Hahn, H. (1973 / 1996) The Scientific Conception of the World: the Vienna Circle, in S. Sarkar (ed.) The Emergence of Logical Empiricism: from 1900 to the Vienna Circle. Garland Publishing, pp. 321–340.

Niiniluoto, I. (1980) Scientific progress. Synthese 45:427-462.

Niiniluoto, I. (1987) 1987, Truthlikeness. D. Reidel.

Niiniluoto, I. (2011) Scientific progress. Stanford Encyclopedia of Philosophy (accessed on 26 June 2012).

Nishitani, K. (1990) The Self-Overcoming of Nihilism. SUNY.

Nolt, J. (1996) Logics. Cengage Learning.

Norton, J.D. (2004) On thought experiments: Is there more to the argument? Philosophy of Science 71:1139–1151.

Nozick, R. (1974) Anarchy, State, and Utopia. Basic Books.

Nozick, R. (1981) Philosophical Explanations. Harvard University Press.

Nussbaum, M. (1997) Cultivating Humanity: A Classical Defense of Reform in Liberal Education. Harvard University Press.

O’Connor, T. (2010) Free will. Stanford Encyclopedia of Philosophy (accessed on 25 August 2015).

Ogle, K. (2009) Hierarchical Bayesian statistics: merging experimental and modeling approaches in ecology. Ecological Applications 19:577-581.

Orr, H.A. (2013) Awaiting a new Darwin. The New York Review of Books, 7 February.

Papineau, D. (2007) Naturalism. Stanford Encyclopedia of Philosophy (accessed on 26 June 2012).

Papineau, D. (2010) Realism, Ramsey sentences and the pessimistic meta-induction. Studies in History and Philosophy of Science, Part A 41:375-385.

Peirce, C.S. (1931–58) The Collected Papers of Charles Sanders Peirce. C. Hartshorne, P. Weiss and A. Burks (eds). Harvard University Press.

Peirce, C.S. 1992 and 1999. The Essential Peirce. Indiana University Press.

Pennock, R.T. (1998) Tower of Babel: Scientific Evidence and the New Creationism. M.I.T. Press.

Pennock, R.T. (2011) Can’t Philosophers Tell the Difference between Science and Religion? Demarcation Revisited. Synthese 178:177–206.

Peters, O. (2014) Degenerate Art: The Attack on Modern Art in Nazi Germany 1937. Prestel.

Phillips, S. (2011) Epistemology in classical Indian philosophy. Stanford Encyclopedia of Philosophy (accessed on 20 July 2012).

Pigliucci, M. (2001) Phenotypic Plasticity: Beyond Nature and Nurture. Johns Hopkins University Press.

Pigliucci, M. (2003) Species as family resemblance concepts the (dis-)solution of the species problem? BioEssays 25:596–602.

Pigliucci, M. (2008) The borderlands between science and philosophy an introduction. Quarterly Review of Biology 83:7-15.

Pigliucci, M. (2010) A misguided attack on evolution. Nature 464:353-354.

Pigliucci, M. (2012) Answers for Aristotle: How Science and Philosophy Can Lead Us to A More Meaningful Life. Basic Books.

Pigliucci, M. and Boudry, M. (2013) Philosophy of Pseudoscience: Reconsidering the Demarcation Problem. University of Chicago Press.

Pigliucci, M. and Kaplan, J. (2006) Making Sense of Evolution: The Conceptual Foundations of Evolutionary Biology. University of Chicago Press.

Pigliucci and Müller (eds.) (2010) Evolution - the Extended Synthesis. MIT Press.

Pinker, S. (1997) How the Mind Works. W.W. Norton & Co.

Plato (circa 399 BCE / 2012) Euthyphro. Translation by Benjamin Jowett. CreateSpace. Platt, J. (1964) Strong inference. Science 146:347-353.

Pohl, R.F. (2012) Cognitive Illusions: A Handbook on Fallacies and Biases in Thinking, Judgement and Memory. Psychology Press.

Popova, M. (2012) What is Philosophy? An Omnibus of Definitions from Prominent Philosophers (accessed on 26 June 2012).

Popper, K. (1963) Conjectures and Refutations: The Growth of Scientific Knowledge. Routledge.

Post, Heinz R. (1971) Correspondence, Invariance and Heuristics. Studies in History and Philosophy of Science 2:213-255.

Priest, G. (2008) An Introduction to Non-Classical Logic: From If to Is. University of Cambridge Press.

Priest, G. (2009) Paraconsistent logic. Stanford Encyclopedia of Philosophy (accessed on 14 September 2012).

Priest, G., Beall, J.C. and Armour-Garb, B. (eds.) (2004) The Law of Non-Contradiction. Oxford University Press.

Putnam, H. (1975) Mathematics, Matter and Method. Cambridge University Press.

Putnam, H. (1978) Meaning and the Moral Sciences. Routledge & Kegan Paul.

Quine, W.V.O. (1960) Word and Object. MIT Press.

Quine, W.V.O. (1980) From A Logical Point of View. Harvard University Press.

Quine, W.V.O. (1991) Two Dogmas in Retrospect. Canadian Journal of Philosophy 21:265-274.

Quine, W.V.O. (1995) Naturalism; or, living within one’s means. Dialectica 49:251-261.

Raatikainen, P. (2015) Gödel's Incompleteness Theorems. Stanford Encyclopedia of Philosophy (accessed on 10 August 2015).

Radford, L. (2014) Reflections on history of mathematics. In: M. Fried and T. Dreyfus (eds.), Mathematics & Mathematics Education: Searching for Common Ground, Springer.

Railton, P. (2003) Facts, Values, and Norms: Essays toward a Morality of Consequence. Cambridge University Press.

Ramsay, S. and Rockwell, G. (2013) “Developing Things: Notes toward an Epistemology of Building in the Digital Humanities,” in: M.K. Gold (ed.), Debates in the Digital Humanities, University of Minnesota Press, pp. 75-84.

Rawls, J. (1971) A Theory of Justice. Belknap Press.

Rescher, N. (1978) Philosophical disagreements: an essay toward orientational pluralism in metaphilosophy. Review of Metaphysics 32:217-251.

Richard, R. (1991) Essays on Heidegger and Others. Cambridge University Press.

Richards, R.J. (2010) Darwin tried and true. American Scientist May-June.

Rorty, R. (1980) Philosophy and the Mirror of Nature. Blackwell.

Rorty, R. (1991) The Priority of Democracy to Philosophy. In: Objectivity, Relativism, and Truth. Philosophical Papers, Volume 1. Cambridge University Press.

Rosenberg, A. (2011) The Atheist's Guide to Reality: Enjoying Life without Illusions. W.W. Norton & Company.

Rosenthal, D.M. (1994) Identity Theories. In: S. Guttenplan (ed.), A Companion to the Philosophy of Mind. Blackwell, 348–355.

Ross, P.E. (2006) The expert mind. Scientific American, July 24.

Ross, D., Ladyman, J., and Kincaid, A. (2013) Scientific Metaphysics. Oxford University Press.

Rowbottom, D.P. (2011) Kuhn vs. Popper on criticism and dogmatism in science: a resolution at the group level. Studies in History and Philosophy of Science, Part A 42:117-124.

Russell, B. (1918) On the scientific method in philosophy. In: Mysticism and Logic and Other Essays. Longmans, Green and Co.

Sarton, G. (1936) The Study of the History of Science. Harvard University Press.

Saunders, S. (1993) To what physics corresponds. In: S. French and H. Kamminga (eds.), Correspondence, Invariance and Heuristics: Essays in Honour Of Heinz Post. Kluwer Academic Press.

Scerri, E. (1991) The electronic configuration model, quantum mechanics and reduction. British Journal for the Philosophy of Science 42:309–325.

Scerri. E. (1994) Has chemistry been at least approximately reduced to quantum mechanics? In: D. Hull, M. Forbes and R. Burian (eds.), PSA 1994 (Vol. 1), Philosophy of Science Association.

Selinger, E. and Crease, R.P. (eds.) (2006) The Philosophy of Expertise. Columbia University Press.

Sidgwick, H. (1874) The Methods of Ethics (accessed on 9 May 2014).

Singer, P. (1972) Famine, affluence, and morality. Philosophy and Public Affairs 1:229-243.

Singer, P. (1997) The Drowning Child and the Expanding Circle. New Internationalist, April (accessed on 9 May 2014).

Singer, P. (2013) The why and how of effective altruism. TED Talk (accessed on 9 May 2014).

Sinnott-Armstrong, W. (2006) Consequentialism. Stanford Encyclopedia of Philosophy (accessed on 13 January 2010).

Smith, R. (1982) What is Aristotelian Ecthesis? History and Philosophy of Logic 3:113–127.

Smolin, L. (2007) The Trouble With Physics: The Rise of String Theory, The Fall of a Science, and What Comes Next. Mariner Books.

Snyder, L.J. (2006) William Whewell. Stanford Encyclopedia of Philosophy (accessed on 12 September 2012).

Snyder, L.J. (2012) Experience and necessity: the Mill-Whewell debate, in: J.R. Brown (ed.), Philosophy of Science: the Key Thinkers. Comtinuum, chapter 1.

Sokal, A. and Bricmont, J. (2003) Intellectual Impostures. Profile Books.

Sorell, T. (1994) Scientism: Philosophy and the Infatuation with Science. Routledge.

Sosa, E. (2009) A defense of the use of intuitions in philosophy. In: M. Bishop & D. Murphy (eds.) Stich and His Critics. Blackwell.

Stadler, F. (2012) The Vienna Circle: Moritz Schlick, Otto Neurath and Rudolf Carnap. In: J.R. Brown (ed.) Philosophy of Science: The Key Thinkers. Continuum, pp. 83-111.

Steup, M. (1999) A Defense of Internalism. In: L.P. Pojman (ed.) The Theory of Knowledge: Classical and Contemporary Readings. Wadsworth, pp. 373–384.

Steup, M. (2005) Epistemology. Stanford Encyclopedia of Philosophy (accessed on 26 June 2012).

Szabó, A. (1968) The Beginnings of Greek Mathematics. Reidel.

Tegmark, M. (2014) Our Mathematical Universe: My Quest for the Ultimate Nature of Reality. Knopf.

Thomas, B.C., Croft, K.E., and Tranel D. (2011) Harming kin to save strangers: further evidence for abnormally utilitarian moral judgments after ventromedial prefrontal damage. Journal of Cognitive Neuroscience 23:2186-2196.

Traweek, S. (1988) Beamtimes and Lifetimes: The World of High Energy Physicists. Harvard University Press.

Unger, P. (2014) Empty Ideas: A Critique of Analytic Philosophy. Oxford University Press.

Unger, R.M. and Smolin, L. (2014) The Singular Universe and the Reality of Time: A Proposal in Natural Philosophy. Cambridge University Press.

van Fraassen, B.C. (1980) The Scientific Image. Oxford University Press.

van Fraassen, B.C. (1989) Laws and Symmetry. Clarendon.

Vicente, A. (2006) On the causal completeness of physics. International Studies in the Philosophy of Science 20:149-171.

Ward, D. (1992) The Role of Satisficing in Foraging Theory. Oikos 63:312-317.

Waters, K. (2007) Molecular genetics. Stanford Encyclopedia of Philosophy (accessed on 6 August 2015).

Weil, A. (1978) History of mathematics: why and how. In: Proceedings of the International Congress of Mathematicians. O. Lehto (ed.), American Mathematical Society, pp. 227-236.

Weinberg, S. (1994) Against philosophy. In: Dreams of a Final Theory: The Scientist's Search for the Ultimate Laws of Nature. Vintage.

Weinberg, S. (2001) Physics and history, In: Labinger, J.A. and Collins, H. (eds.) The One Culture?: A Conversation about Science, Chapter 9. University Of Chicago Press.

Weisberg, M. and Leiter, B. (2012) Do You Only Have a Brain? On Thomas Nagel. The Nation, 22 October.

Weisberg, M., Needham, P., and Hendry, R. (2011) Philosophy of chemistry. Stanford Encyclopedia of Philosophy (accessed on 6 August 2015).

Whewell, W. (1847) Philosophy of the Inductive Sciences. John W. Parker.

Whitehead, A.N. and Russell, B. (1910) Principia Mathematica. Cambridge University Press.

Wilkins, J. (2009) Species: The history of the idea. University of California Press.

Williamson, T. (2005) Armchair philosophy, metaphysical modality and counterfactual thinking. Proceedings of the Aristotelian Society 105:1-23.

Williamson, T. (2013) Review of Experimental Philosophy: An Introduction. By Joshua Alexander. Philosophy 88:467-474.

Wilson, J.G. (2013) Alfred Russel Wallace and Charles Darwin: perspectives on natural selection. Transactions of the Royal Society of South Australia 137:90-95.

Wimsatt, W.C. (2007) Re-Engineering Philosophy for Limited Beings: Piecewise Approximations to Reality. Harvard University Press.

Wittgenstein, L. (1921) Tractatus Logicus-Philosophicus (accessed on 8 February 2013).

Wittgenstein, L. (1953 / 2009) Philosophical Investigations. Wiley-Blackwell.

Wittgenstein, L. (1965) The Blue and Brown Books. Harper and Row.

Woitt, P. (2006) Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law for Unity in Physical Law. Basic Books.

Wong, D. (2009) Comparative philosophy: Chinese and Western. Stanford Encyclopedia of Philosophy (accessed on 19 July 2012).

Worrall, J. (1989) Structural realism: The best of both worlds? Dialectica, 43: 99–124.

Worrall, J. (2012) Miracles and structural realism. The Western Ontario Series in Philosophy of Science 77:77-95.

Young, J.O. (2013) The coherence theory of truth. Stanford Encyclopedia of Philosophy (accessed on 4 June 2013).

Yu, J. (2007) The Ethics of Confucius and Aristotle. Routledge.

Zadeh, L.A. (1988) Fuzzy logic. Computer 21:83-93.

Zaretsky, R. (2009) The Philosophers' Quarrel: Rousseau, Hume, and the Limits of Human Understanding. Yale University Press.

Zupko, J. (2003) John Buridan: Portrait of a Fourteenth-Century Arts Master, Publications in Medieval Studies, University of Notre Dame Press.

Zupko, J. (2014) John Buridan. Stanford Encyclopedia of Philosophy (accessed on 28 August 2014).

About the Author

Massimo Pigliucci is the K.D. Irani Professor of Philosophy at the City College of New York. His academic work is in evolutionary biology, philosophy of science, the nature of pseudoscience, and the practical philosophy of Stoicism. His books include How to Be a Stoic: Using Ancient Philosophy to Live a Modern Life (Basic Books) and Nonsense on Stilts: How to Tell Science from Bunk (University of Chicago Press). His most recent book is A Field Guide to a Happy Life: 53 Brief Lessons for Living (Basic Books). More by Massimo at figsinwinter.blog.

[1] I am grateful to Dan Tippens for this example.

[2] Although see also the delightful dialogue by Hansson (2012), featuring a graduate student and two professors of philosophy traveling with him to a conference on teaching philosophy.

[3] Interestingly, from the Greek aporetikos, which means impassable, very difficult, or hard to deal with.

[4] Interestingly, that empirical result depends on one’s definition of happiness: the research shows that people’s moment-to-moment feelings are negatively affected by the presence of children, but also that their self-satisfaction with the trajectory of their lives is higher if they have children. The ancient Greeks would have called the latter type of happiness eudaimonia, or flourishing, and they would have rejected its confusion with the former, hedonic, concept.

[5] Of course, it would be perfectly legitimate to claim logic as a branch of philosophy, show that the former makes progress and therefore claim that philosophy does too. But that would be too easy, and I prefer challenging propositions.

[6] I can see some of my esteemed colleagues rolling their eyes at the very mention of Wikipedia. Relax. First, the available empirical evidence is actually that — at least as far as science entries are concerned (and there is little reason to think that philosophical ones are different) — Wikipedia is about as accurate as the Encyclopedia Britannica (Giles 2005). Second, the data I am about to present is merely meant as illustrative of the possibilities, as such a study could be replicated using more scholarly sources, such as the Stanford Encyclopedia of Philosophy.

[7] I recognize that the terms “proto-continental” and “proto-analytical” are not part of the standard philosophical jargon. Consider them my modest contribution to the debate. I am confident that my fellow philosophers will recognize immediately why certain figures do indeed belong to those (albeit fuzzy) categories

[8] I would go even further and argue that part of the reason practitioners of other approaches wish to use the term “philosophy” is because of the huge cultural cachet that derives from an association with Socrates, Plato, Aristotle and all the others. And I do not say this out of cultural chauvinism, since I am Italian, not Greek.

[9] That said, my colleague Graham Priest and I have amiably disagreed in public on the relationship between Buddhism and logic: see my contribution, based on a previous essay of his, and his response to me.

[10] We are, of course, talking about philosophical mood, not the psychological profiles of the individuals involved — though that would perhaps be an excellent topic of research for experimental philosophers.

[11] The discontinuity between the early and late Wittgenstein, however, should not be overplayed. As several commentators have pointed out, for instance, both the Tractatus and the Investigations are very much concerned with the idea that a primary task of philosophy is the critique of language.

[12] As Kripke himself put it: “I don’t have the prejudices many have today, I don’t believe in a naturalist world view. I don’t base my thinking on prejudices or a worldview and do not believe in materialism.” Quoted in “Saul Kripke, Genius Logician,” David Boles Blogs, 25 February 2001.

[13] As Papineau himself clarifies, this is not the same distinction that is often brought up in discussions of whether science can test supernatural claims. In that context, ontological (sometimes referred to as “philosophical”) naturalism is the philosophical position that there is no supernatural realm, while methodological naturalism is the provisional assumption — necessary for doing science, according to many — that even if the supernatural exists it cannot enter scientific theorizing at any level, on penalty of giving up the very meaning of scientific explanation.

[14] It should be obvious that truth as understood here is a property of propositions and statements, but not of other things. “The truth,” then, is not a concrete entity to be found, nor is it an abstract object apart from the class of true propositions.

[15] However, we will see in a bit about Gettier-type objections to the standard view of what constitutes knowledge.

[16] This really only describes half of the meta-induction, and the less controversial half at that; we should note that the meta-induction concludes that all future theories will also turn out to be false.

[17] Perhaps a useful way to think about this is to realize that there is no sense in which we can say, for example, that Darwinian evolution is closer to the truth than Newtonian mechanics, since they don’t share the same framework, and are not concerned with the same cognitive problem.

[18] See my lay summary of this in: Are there natural laws?, by M. Pigliucci, Rationally Speaking, 3 October 2013 (accessed on 6 August 2015).

[19] Interestingly, some physicists (Smolin 2007) seem to provide support for Cartwright’s contention, to a point. In his The Trouble with Physics Smolin speculates that there are empirically intriguing reasons to suspect that Special Relativity “breaks down” at very high energies, which means that it would not be a law of nature in the “fundamental” sense, only in the “phenomenological” one. He also suggests that General Relativity may break down at very large cosmological scales.

[20] Yes, I realize that this and the next citation refer to blog posts, not peer reviewed papers. We live in a brave new world, and sometimes interesting ideas are put out there in the blogosphere. More seriously, sometimes comments blogged by professionals in a field are more informative and insightful than what they write in the primary literature, for the simple fact that they can afford to lower their guard somewhat, expressing themselves more freely and creatively. I know because I do a lot of blogging myself...

[21] We will not get into a discussion of what constitutes “sanity” insofar as possibility #5 is concerned. Another time, perhaps.

[22] I am indebted to an anonymous reviewer for bringing up these examples in her/his critique of a previous draft of this chapter.

[23] Which says: if a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

[24] Complex numbers of the form w + xi + yj + zk, where w, x, y, z are real numbers and i, j, k are imaginary units that satisfy certain conditions.

[25] For more recent entries on the history of mathematics, see, among others: Krantz, 2010; Cooke 2011; Radford 2014. On the related (as far as concepts of progress go) field of the philosophy of mathematics, see: Irvine, 2009; Colyvan 2012.

[26] Full disclosure: I fall squarely in the camp of those targeted by Lynch.

[27] The discoveries of the Higgs boson in 2013 and of gravitational waves in 2016 do not count, since they (spectacularly) confirmed the already established Standard Model and General Theory of Relativity, respectively.

[28] If you really wish to know, the claim is that V-E + F = 2, where V is the number of vertices, E the number of edges, and F the number of faces.

[29] It may have occurred to some readers that a number of scientists seem to think that mathematics actually is a science, because it historically got started with empirical observations about the geometric-mathematical properties of the world. I refer to this (misguided) view as radical empiricism. Here are my thoughts on the matter.

[30] On the not exactly crystalline topic of ekthesis, see: Smith, 1982.

[31] A logical explosion is a situation where everything follows from a contradiction, which is possible within the standard setup of classical logic.

[32] However, a recent paper by Machery et al. (2015) shows that most non-philosophers do not consider Gettier cases to be instances of knowledge. Moreover, there seems to be no cross-cultural disagreement on this verdict.

[33] You can see how you can generate concept maps of different aspects of discussions about justification, and then proceed to connect distinct conceptual peaks on each map to positions on other maps with which they cohere. I suspect someone could turn this into a really nerdy video game...

[34] How are you doing with that concept map, so far?

[35] The Greek King Pyrrhus of Epirus was one of my favorite historical villains when I was in elementary school and studied ancient Roman history (the Romans, of course, were the good guys for someone growing up in the Eternal City). He did manage the then inconceivable feat of defeating the Roman legions in open battle, especially thanks to his innovation of bringing in elephants — monsters that were hitherto unknown to the Romans. But his victory at Asculum in 279 BCE caused him so many casualties that he had to acknowledge having lost the war.

[36] Although an argument could be made that this is not the most charitable reading of Moore. One could read him instead as putting forth an evidentialist argument: we have evidence that we have hands, but no evidence that we are being deceived.

[37] I know, I know, this is becoming to sound rather Clintonesque. Then again, the former President of the United States did study philosophy at Oxford as a Rhodes Scholar...

[38] For a general framework comparing the major ethical theories, thus better situating utilitarianism, see here (accessed on 19 November 2015).

[39] Of course, one could simply bite the bullet on this one. But I’m more sympathetic to Mill’s attempt, if not necessarily to the specific way he went about it.

[40] Note that I am not actually attempting to adjudicate the soundness of any of the above moves over any of their rivals. As I said, I do not actually buy into a consequentialist ethical framework (my preference goes to virtue ethics). The point is simply that modern utilitarianism is better (i.e., it has made progress) because of this ongoing back and forth with its critics, which has led utilitarians to constantly refine their positions, and in some cases to abandon some aspects of their doctrine.

[41] I do hope you will immediately agree that if you did act as described above you would behave like a psychopathic monster and you should be locked away for good, so this is just a thought experiment for illustrative purposes. Then again, a study by Bartels and Pizarro (2011) did show a link between utilitarianism and sociopathic traits... Although one by Kahane et al. (2015) actually shades significant doubt on that sort of findings.

[42] Joshua has also graciously agreed to be on my Rationally Speaking podcast, where he made several of his points very cogently.

[43] As an aside, I’m not sure why XPhi — and, as we shall see, the Digital Humanities — label themselves as “movements” rather than methods or approaches. I feel that talk of “movements” unnecessarily fuels an adversarial stance on both sides of these debates.

[44] I have written on scientism in several places, see for instance: Staking positions amongst the varieties of scientism, Scientia Salon, 28 April 2014, accessed on 27 August 2014; Steven Pinker embraces scientism. Bad move, I think, Rationally Speaking, 12 August 2013, accessed on 27 August 2014. I am currently co-editing a book on the topic (together with Maarten Boudry) for the University of Chicago Press.

[45] THATCamp, accessed on 27 August 2014.

[46] See: Where Are the Philosophers? Thoughts from THATCamp Pedagogy, by P. Bradley, accessed on 27 August 2014.

[47] PhilPapers, accessed on 27 August 2014.

[48] PhilJobs, accessed on 27 August 2014.

[49] NGrams, accessed on 27 August 2014.

[50] Although, somewhat disconcertingly, only 20 times less so.

[51] This also raises the question of whether or not the citations are positive or negative, and what that assessment would say about relative importance.

[52] See: Exploring the Significance of Digital Humanities for Philosophy, by Lisa M. Spiro, accessed on 27 August 2014.

[53] The Philosopher's Imprint, accessed on 27 August 2014.

[54] Philosophy & Theory in Biology, accessed on 27 August 2014.

[55] The Stanford Encyclopedia of Philosophy, accessed on 27 August 2014; The Internet Encyclopedia of Philosophy, accessed on 26 August 2015.

[56] I criticize the excessive embracing of evolutionary psychology and other sciences in the humanities here: Who knows what, Aeon Magazine, accessed on 27 August 2014.

[57] You will have noticed that a significant portion of the debate surrounding the DH takes place in the public sphere, not in peer reviewed papers. Welcome to the new academy.

[58] I have often encountered this very same tendency during my practice as an evolutionary biologist, before turning to philosophy full time. It is such a general phenomenon that it has an informal name: the streetlight effect, as in someone looking for his lost keys near the streetlight, regardless of where he actually lost them, because that’s where he can see best.

[59] Goldman does add the caveat that many philosophical discussions are about folk- ontological concepts, not technical terms. I submit, however, that philosophical discussions of this type begin with folk-ontological concepts, but then mold them in a way that transforms them into technical terms. It is at that point that philosophical expertise becomes paramount and that laypeople’s understanding of the newly molded concept becomes pretty much irrelevant to philosophical inquiry. Unfortunately, the frequent lack of appreciation that philosophers and laypeople may be using the same words but meaning different things ends up generating a lot of unnecessary confusion.

[60] As a philosopher of science, I also found interesting that colleagues in my field turned out to think that the role of intuition in justification in the course of their practice is far less important than philosophers who work on epistemology, ethics, metaphysics and philosophy of mind.

[61] As one can see, it is really difficult to get away from the i-word in philosophy, no matter how hard one tries!

Massimo Pigliucci

The Nature of Philosophy How Philosophy Makes Progress and Why It Matters

Publisher Details

Introduction — Read This First...